ถ้าคุณต้องการพัฒนาการวิเคราะห์ทางสถิติหรือทางวิศวกรรมที่ซับซ้อน คุณสามารถประหยัดขั้นตอนและเวลาได้โดยใช้ Analysis ToolPak คุณให้ข้อมูลและพารามิเตอร์สําหรับการวิเคราะห์แต่ละครั้ง และเครื่องมือจะใช้ฟังก์ชันแมโครทางสถิติหรือวิศวกรรมที่เหมาะสมเพื่อคํานวณและแสดงผลลัพธ์ในตารางผลลัพธ์ เครื่องมือบางอย่างจะสร้างแผนภูมินอกเหนือจากตารางผลลัพธ์
ฟังก์ชันการวิเคราะห์ข้อมูลสามารถใช้บนเวิร์กชีตได้ครั้งละหนึ่งเวิร์กชีตเท่านั้น เมื่อคุณทําการวิเคราะห์ข้อมูลบนเวิร์กชีตที่ถูกจัดกลุ่ม ผลลัพธ์จะปรากฏบนเวิร์กชีตแรก และตารางที่จัดรูปแบบว่างเปล่าจะปรากฏบนเวิร์กชีตที่เหลือ เมื่อต้องการทําการวิเคราะห์ข้อมูลในส่วนที่เหลือของเวิร์กชีต ให้คํานวณเครื่องมือการวิเคราะห์สําหรับแต่ละเวิร์กชีตใหม่
Analysis ToolPak ประกอบด้วยเครื่องมือที่อธิบายไว้ในส่วนต่อไปนี้ เมื่อต้องการเข้าถึงเครื่องมือเหล่านี้ ให้คลิก การวิเคราะห์ข้อมูล ในกลุ่ม วิเคราะห์ บนแท็บ ข้อมูล ถ้าคําสั่ง การวิเคราะห์ข้อมูล ไม่พร้อมใช้งาน คุณจําเป็นต้องโหลดโปรแกรม Analysis ToolPak Add-in
-
คลิกแท็บ ไฟล์ คลิก ตัวเลือก แล้วคลิกประเภท Add-in
-
ในกล่อง จัดการ ให้เลือก Add-ins ของ Excel แล้วคลิก ไป
ถ้าคุณกําลังใช้ Excel for Mac ในเมนูไฟล์ ให้ไปที่ เครื่องมือ > Add-in ของ Excel
-
ในกล่อง Add-in ให้เลือกกล่องกาเครื่องหมาย Analysis ToolPak แล้วคลิก ตกลง
-
ถ้า Analysis ToolPak ไม่อยู่ในกล่อง Add-in ที่มีอยู่ ให้คลิก เรียกดู เพื่อระบุตำแหน่ง Analysis ToolPak
-
ถ้าคุณได้รับการแจ้งเตือนว่ายังไม่ได้ติดตั้ง Analysis ToolPak ในคอมพิวเตอร์ของคุณ ให้คลิก ใช่ เพื่อติดตั้ง Analysis ToolPak
-
หมายเหตุ: เมื่อต้องการรวมฟังก์ชัน Visual Basic for Application (VBA) สําหรับ Analysis ToolPak คุณสามารถโหลด Add-in Analysis ToolPak - VBA ในลักษณะเดียวกับที่คุณโหลด Analysis ToolPak ในกล่อง Add-in ที่มีอยู่ ให้เลือกกล่องกาเครื่องหมาย Analysis ToolPak - VBA
เครื่องมือการวิเคราะห์ Anova มีการวิเคราะห์ค่าความแปรปรวนชนิดต่างๆ เครื่องมือที่คุณควรใช้จะขึ้นอยู่กับจํานวนปัจจัยและจํานวนตัวอย่างที่คุณมีจากประชากรที่คุณต้องการทดสอบ
Anova: ปัจจัยเดียว
เครื่องมือนี้จะทําการวิเคราะห์อย่างง่ายเกี่ยวกับค่าความแปรปรวนของข้อมูลสําหรับตัวอย่างอย่างน้อยสองตัวอย่าง การวิเคราะห์จะให้การทดสอบสมมติฐานว่าแต่ละตัวอย่างถูกดึงมาจากการแจกแจงความน่าจะเป็นแบบเดียวกันเทียบกับสมมติฐานสํารองว่าการแจกแจงความน่าจะเป็นพื้นฐานไม่เหมือนกันสําหรับตัวอย่างทั้งหมด ถ้ามีเพียงสองตัวอย่าง คุณสามารถใช้ฟังก์ชันเวิร์กชีต Tได้ทดสอบ. ด้วยตัวอย่างมากกว่าสองตัวอย่างไม่มีความสะดวกในการใช้งานทั่วไปของ Tการทดสอบ, และเดียวปัจจัย anova รูปแบบสามารถเรียกแทนของ
Anova: สองปัจจัยที่มีการจำลองแบบ
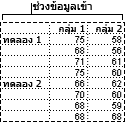
เครื่องมือการวิเคราะห์นี้มีประโยชน์เมื่อสามารถจัดประเภทข้อมูลได้สองขนาดที่แตกต่างกัน ตัวอย่างเช่นในการทดลองเพื่อวัดความสูงของพืชพืชอาจได้รับปุ๋ยยี่ห้อต่าง ๆ (ตัวอย่างเช่น A, B, C) และอาจเก็บไว้ในอุณหภูมิที่แตกต่างกัน (ตัวอย่างเช่นต่ําสูง) สําหรับ {ปุ๋ย, อุณหภูมิ} ที่เป็นไปได้หกคู่ เรามีการสังเกตความสูงของพืชเท่ากัน เมื่อใช้เครื่องมือ Anova นี้ เราสามารถทดสอบ:
-
ความสูงของพืชสําหรับแบรนด์ปุ๋ยที่แตกต่างกันนั้นถูกวาดจากประชากรที่เป็นพื้นฐานเดียวกันหรือไม่ อุณหภูมิจะถูกละเว้นสําหรับการวิเคราะห์นี้
-
ความสูงของพืชสําหรับระดับอุณหภูมิที่แตกต่างกันนั้นถูกวาดจากประชากรที่เป็นพื้นฐานเดียวกันหรือไม่ แบรนด์ปุ๋ยจะถูกละเว้นสําหรับการวิเคราะห์นี้
ไม่ว่าจะคํานึงถึงผลกระทบของความแตกต่างระหว่างตราสินค้าของปุ๋ยที่พบในสัญลักษณ์แสดงหัวข้อย่อยจุดแรกและความแตกต่างของอุณหภูมิที่พบในสัญลักษณ์แสดงหัวข้อย่อยที่สองตัวอย่างหกตัวอย่างที่แสดงค่า {ปุ๋ย, อุณหภูมิ} ทุกคู่จะถูกวาดจากประชากรเดียวกัน สมมติฐานอื่นคือมีผลเนื่องจาก {ปุ๋ย, อุณหภูมิ} คู่ที่เฉพาะเจาะจงมากกว่าและสูงกว่าความแตกต่างที่ใช้ปุ๋ยเพียงอย่างเดียวหรืออุณหภูมิเพียงอย่างเดียว
Anova: สองปัจจัยที่ไม่มีการจำลองแบบ
เครื่องมือการวิเคราะห์นี้มีประโยชน์เมื่อข้อมูลถูกจัดประเภทบนสองขนาดที่แตกต่างกันเช่นในกรณี Two-Factor ด้วยการจําลองแบบ อย่างไรก็ตามสําหรับเครื่องมือนี้จะสันนิษฐานว่ามีเพียงข้อสังเกตเดียวสําหรับแต่ละคู่ (ตัวอย่างเช่น แต่ละคู่ {ปุ๋ย, อุณหภูมิ} ในตัวอย่างก่อนหน้านี้)
ฟังก์ชันเวิร์กชีต CORREL และ PEARSON จะคํานวณสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรการวัดสองตัว เมื่อการวัดบนแต่ละตัวแปรถูกสังเกตได้สําหรับแต่ละหัวข้อ N (ข้อสังเกตใด ๆ ที่หายไปสําหรับสาเหตุใด ๆ ที่อาจมีการละเว้นในการวิเคราะห์) เครื่องมือการวิเคราะห์สหสัมพันธ์มีประโยชน์เป็นพิเศษเมื่อมีตัวแปรการวัดมากกว่าสองตัวแปรสําหรับแต่ละหัวข้อ N ซึ่งจะให้ตารางผลลัพธ์ ซึ่งเป็นเมทริกซ์สหสัมพันธ์ ที่แสดงค่า ของ CORREL (หรือ PEARSON) ที่ใช้กับตัวแปรการวัดที่เป็นไปได้แต่ละคู่
ค่าสัมประสิทธิ์สหสัมพันธ์ เช่น ค่าความแปรปรวนร่วม เป็นการวัดขอบเขตที่ตัวแปรการวัดสองตัว "แตกต่างกันด้วยกัน" ค่าสัมประสิทธิ์สหสัมพันธ์จะต่างจากค่าความแปรปรวนร่วม ดังนั้น ค่าของค่าสหสัมพันธ์จึงไม่ขึ้นอยู่กับหน่วยที่แสดงตัวแปรการวัดสองตัว (ตัวอย่างเช่น ถ้าตัวแปรการวัดสองตัวคือน้ําหนักและความสูง ค่าของสัมประสิทธิ์สหสัมพันธ์จะไม่เปลี่ยนแปลง ถ้าน้ําหนักถูกแปลงจากปอนด์เป็นกิโลกรัม) ค่าของสัมประสิทธิ์สหสัมพันธ์ใดๆ ต้องอยู่ระหว่าง -1 และ +1
คุณสามารถใช้เครื่องมือวิเคราะห์สหสัมพันธ์ เพื่อตรวจสอบคู่ตัวแปรการวัดแต่ละคู่ เมื่อต้องการระบุว่าตัวแปรการวัดสองตัวมีแนวโน้ม "แปรตามกัน" หรือไม่ นั่นก็คือ ตัวแปรหนึ่งที่มีค่ามากมีแนวโน้มจะสัมพันธ์กับอีกตัวแปรที่มีค่ามากหรือไม่ (สหสัมพันธ์บวก) ตัวแปรหนึ่งที่มีค่าน้อยมีแนวโน้มจะสัมพันธ์กับอีกตัวแปรที่มีค่ามากหรือไม่ (สหสัมพันธ์ลบ) หรือค่าของทั้งสองตัวแปรมีแนวโน้มที่จะไม่สัมพันธ์กัน (สหสัมพันธ์เข้าใกล้ 0 (ศูนย์))
เครื่องมือสหสัมพันธ์และค่าความแปรปรวนร่วมสามารถใช้ในการตั้งค่าเดียวกันได้ทั้งคู่ เมื่อคุณสังเกตเห็นตัวแปรการประเมิน N ที่แตกต่างกันในแต่ละชุด เครื่องมือสหสัมพันธ์และค่าความแปรปรวนร่วมจะให้ตารางผลลัพธ์ เมทริกซ์ ที่แสดงสัมประสิทธิ์สหสัมพันธ์หรือค่าความแปรปรวนร่วม ตามลําดับระหว่างตัวแปรการวัดแต่ละคู่ ความแตกต่างคือสัมประสิทธิ์สหสัมพันธ์จะถูกปรับมาตราส่วนให้อยู่ระหว่าง -1 และ +1 ค่าความแปรปรวนร่วมที่สอดคล้องกันจะไม่ถูกปรับมาตราส่วน ทั้งค่าสัมประสิทธิ์สหสัมพันธ์และค่าความแปรปรวนร่วมเป็นการวัดขอบเขตที่ตัวแปรสองตัว "แตกต่างกัน"
เครื่องมือค่าความแปรปรวนร่วมจะคํานวณค่าของฟังก์ชันเวิร์กชีต COVARIANCE P สําหรับแต่ละคู่ของตัวแปรการวัด (การใช้งานโดยตรงของค่าความแปรปรวนร่วม P แทนเครื่องมือความแปรปรวนร่วมเป็นทางเลือกที่เหมาะสมเมื่อมีตัวแปรการวัดเพียงสองตัวแปร นั่นคือ N=2) รายการบนเส้นทแยงมุมของตารางผลลัพธ์ของเครื่องมือค่าความแปรปรวนร่วมในแถว i คอลัมน์ i คือค่าความแปรปรวนร่วมของตัวแปรการวัดในลําดับที่ i ค่านี้เป็นเพียงค่าความแปรปรวนของประชากรสําหรับตัวแปรนั้น ดังที่คํานวณโดยฟังก์ชันเวิร์กชีต VARพี.
คุณสามารถใช้เครื่องมือวิเคราะห์ความแปรปรวนร่วม เพื่อตรวจสอบคู่ตัวแปรการวัดแต่ละคู่ เมื่อต้องการระบุว่าตัวแปรการวัดสองตัวมีแนวโน้ม "แปรตามกัน" หรือไม่ นั่นก็คือ ตัวแปรหนึ่งที่มีค่ามากมีแนวโน้มจะสัมพันธ์กับอีกตัวแปรที่มีค่ามากหรือไม่ (สหสัมพันธ์บวก) ตัวแปรหนึ่งที่มีค่าน้อยมีแนวโน้มจะสัมพันธ์กับอีกตัวแปรที่มีค่ามากหรือไม่ (สหสัมพันธ์ลบ) หรือค่าของทั้งสองตัวแปรมีแนวโน้มที่จะไม่สัมพันธ์กัน (สหสัมพันธ์เข้าใกล้ 0 (ศูนย์))
เครื่องมือวิเคราะห์สถิติเชิงพรรณนาจะสร้างรายงานของสถิติหนึ่งตัวแปรสำหรับข้อมูลในช่วงข้อมูลเข้า โดยมีข้อมูลเกี่ยวกับแนวโน้มเข้าสู่ส่วนกลางและการแปรผันของข้อมูลของคุณ
เครื่องมือการปรับเรียบแบบเอ็กซ์โพเนนเชียลทํานายค่าที่ยึดตามการพยากรณ์สําหรับช่วงเวลาก่อนหน้า ซึ่งได้รับการปรับปรุงสําหรับข้อผิดพลาดในการพยากรณ์ก่อนหน้านี้ เครื่องมือใช้ค่าคงที่ปรับเรียบ a ขนาดของค่าที่กําหนดว่าการคาดการณ์ตอบสนองต่อข้อผิดพลาดในการพยากรณ์ก่อนหน้านี้มากเพียงใด
หมายเหตุ: ค่า 0.2 ถึง 0.3 เป็นค่าคงที่ปรับเรียบที่เหมาะสม ค่าเหล่านี้ระบุว่าการคาดการณ์ปัจจุบันควรได้รับการปรับปรุง 20 เปอร์เซ็นต์เป็น 30 เปอร์เซ็นต์สําหรับข้อผิดพลาดในการพยากรณ์ก่อนหน้านี้ ค่าคงที่ที่ใหญ่ขึ้นจะให้การตอบสนองที่เร็วขึ้น แต่สามารถสร้างการฉายที่ผิดปกติได้ ค่าคงที่ที่น้อยกว่าอาจส่งผลให้ค่าการพยากรณ์ล่าช้า
เครื่องมือการวิเคราะห์ความแปรปรวนแบบ F-Test สองตัวอย่าง จะดำเนินการ F-test แบบสองตัวอย่างเพื่อเปรียบเทียบความแปรปรวนของประชากรสองกลุ่ม
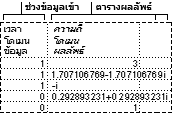
ตัวอย่างเช่น คุณสามารถใช้เครื่องมือ F-Test กับตัวอย่างของเวลาในการว่ายน้ําสําหรับทีมแต่ละทีม เครื่องมือจะให้ผลลัพธ์ของการทดสอบสมมติฐาน Null ว่าตัวอย่างทั้งสองนี้มาจากการแจกแจงที่มีค่าความแปรปรวนเท่ากันเทียบกับค่าความแปรปรวนไม่เท่ากันในการแจกแจงพื้นฐาน
เครื่องมือจะคํานวณค่า f ของ F-statistic (หรือ F-ratio) ค่า f ที่ใกล้เคียงกับ 1 จะแสดงหลักฐานว่าค่าความแปรปรวนของประชากรพื้นฐานเท่ากับ ในตารางผลลัพธ์ ถ้า f < 1 "P(F <= f) ด้านเดียว" จะทําให้ค่าของค่าสถิติ F น้อยกว่า f เมื่อค่าความแปรปรวนของประชากรเท่ากัน และ "F Critical one-tail" จะให้ค่าวิกฤตที่น้อยกว่า 1 สําหรับระดับนัยสําคัญที่เลือก Alpha ถ้า f > 1, "P(F <= f) ด้านเดียว" จะทําให้ความน่าจะเป็นของการสังเกตค่าของสถิติ F ที่มากกว่า f เมื่อค่าความแปรปรวนของประชากรเท่ากับ และ "F Critical one-tail" จะให้ค่าวิกฤตที่มากกว่า 1 สําหรับ Alpha
เครื่องมือการวิเคราะห์แบบฟูเรียร์จะแก้ไขปัญหาในระบบเชิงเส้น และวิเคราะห์ข้อมูลเป็นระยะโดยใช้วิธี Fast Fourier Transform (FFT) เพื่อแปลงข้อมูล เครื่องมือนี้ยังสนับสนุนการแปลงผกผัน ซึ่งค่าผกผันของข้อมูลที่แปลงจะส่งกลับข้อมูลต้นฉบับ
เครื่องมือการวิเคราะห์ฮิสโตแกรมจะคํานวณความถี่แต่ละความถี่และความถี่สะสมสําหรับช่วงเซลล์ของข้อมูลและถังข้อมูล เครื่องมือนี้จะสร้างข้อมูลสําหรับจํานวนครั้งของค่าในชุดข้อมูล
ตัวอย่างเช่น ในชั้นเรียนที่มีนักเรียน 20 คน คุณสามารถกําหนดการแจกแจงคะแนนในประเภทเกรดเป็นตัวอักษรได้ ตารางฮิสโตแกรมจะแสดงขอบเขตของเกรดตัวอักษรและจํานวนคะแนนระหว่างขอบเขตต่ําสุดและขอบเขตปัจจุบัน คะแนนเดียวที่ใช้บ่อยที่สุดคือโหมดของข้อมูล
เครื่องมือการวิเคราะห์ค่าเฉลี่ยเคลื่อนที่จะประมาณค่าในช่วงการพยากรณ์ โดยยึดตามค่าเฉลี่ยของตัวแปรในจํานวนช่วงเวลาก่อนหน้าที่ระบุ ค่าเฉลี่ยเคลื่อนที่จะให้ข้อมูลแนวโน้มที่ค่าเฉลี่ยอย่างง่ายของข้อมูลในอดีตทั้งหมดจะมาสก์ ใช้เครื่องมือนี้เพื่อคาดการณ์ยอดขาย สินค้าคงคลัง หรือแนวโน้มอื่นๆ ค่าการพยากรณ์แต่ละค่าจะยึดตามสูตรต่อไปนี้
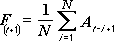
โดยที่
-
N คือจำนวนคาบก่อนหน้าที่จะรวมไว้ในค่าเฉลี่ยเคลื่อนที่
-
A j เป็นค่าจริง ณ เวลา j
-
F j เป็นค่าพยากรณ์ ณ เวลา j
เครื่องมือการวิเคราะห์การสร้างหมายเลขสุ่มจะเติมช่วงด้วยตัวเลขสุ่มที่เป็นอิสระจากหนึ่งในการแจกแจงหลายรายการ คุณสามารถระบุหัวข้อในประชากรที่มีการแจกแจงความน่าจะเป็นได้ ตัวอย่างเช่น คุณสามารถใช้การแจกแจงปกติเพื่อระบุจํานวนประชากรความสูงของแต่ละบุคคล หรือคุณสามารถใช้การแจกแจงเบอร์นูลีของผลลัพธ์ที่เป็นไปได้สองแบบเพื่อระบุจํานวนประชากรของผลลัพธ์แบบพลิกเหรียญ
เครื่องมือการวิเคราะห์อันดับและเปอร์เซ็นต์ไทล์จะสร้างตารางที่มีลําดับเลขลําดับและเปอร์เซ็นต์ของแต่ละค่าในชุดข้อมูล คุณสามารถวิเคราะห์จุดยืนสัมพัทธ์ของค่าต่างๆ ในชุดข้อมูลได้ เครื่องมือนี้ใช้ฟังก์ชันเวิร์กชีต RANK EQ และPERCENTRANK INC. ถ้าคุณต้องการลงบัญชีสําหรับค่าที่เชื่อมโยง ให้ใช้ RANK ฟังก์ชัน EQ ซึ่งถือว่าค่าที่ผูกไว้เป็นลําดับเดียวกัน หรือใช้ ฟังก์ชัน RANKฟังก์ชัน AVG ซึ่งส่งกลับอันดับเฉลี่ยของค่าที่ผูก
เครื่องมือการวิเคราะห์การถดถอยจะทําการวิเคราะห์การถดถอยเชิงเส้นโดยใช้วิธี "กําลังสองน้อยที่สุด" เพื่อให้พอดีกับเส้นผ่านชุดของการสังเกต คุณสามารถวิเคราะห์ว่าตัวแปรที่ไม่เป็นอิสระตัวเดียวได้รับผลกระทบจากค่าของตัวแปรอิสระหนึ่งตัวหรือมากกว่าได้อย่างไร ตัวอย่างเช่นคุณสามารถวิเคราะห์ประสิทธิภาพของนักกีฬาที่ได้รับผลกระทบจากปัจจัยเช่นอายุความสูงและน้ําหนัก คุณสามารถแบ่งส่วนแบ่งในการวัดประสิทธิภาพการทํางานให้กับปัจจัยทั้งสามนี้ โดยยึดตามชุดข้อมูลประสิทธิภาพการทํางาน แล้วใช้ผลลัพธ์เพื่อทํานายประสิทธิภาพการทํางานของนักกีฬาใหม่ที่ยังไม่ได้ทําการทดสอบ
เครื่องมือการถดถอยจะใช้ฟังก์ชันเวิร์กชีต LINEST
เครื่องมือการวิเคราะห์การสุ่มตัวอย่างจะสร้างตัวอย่างจากประชากรโดยถือว่าช่วงข้อมูลเข้าเป็นประชากร เมื่อประชากรมีขนาดใหญ่เกินกว่าที่จะประมวลผลหรือสร้างแผนภูมิ ได้ คุณสามารถใช้ตัวอย่างที่เป็นตัวแทนได้ คุณยังสามารถสร้างตัวอย่างที่มีเฉพาะค่าจากส่วนใดส่วนหนึ่งของรอบถ้าคุณเชื่อว่าข้อมูลป้อนเข้าเป็นข้อมูลประจํางวด ตัวอย่างเช่น ถ้าช่วงข้อมูลเข้ามีตัวเลขยอดขายรายไตรมาส การสุ่มตัวอย่างที่มีอัตราเป็นงวดสี่จะวางค่าจากไตรมาสเดียวกันในช่วงผลลัพธ์
การทดสอบเครื่องมือการวิเคราะห์ t-Test Two-Sample เพื่อความเท่าเทียมกันของประชากรหมายความว่าต้องเน้นแต่ละตัวอย่าง เครื่องมือทั้งสามนี้ใช้สมมติฐานที่แตกต่างกัน: ค่าความแปรปรวนของประชากรเท่ากับค่าความแปรปรวนของประชากรไม่เท่ากัน และตัวอย่างทั้งสองนี้แสดงถึงการสังเกตก่อนการรักษาและหลังการรักษาในหัวข้อเดียวกัน
สําหรับเครื่องมือทั้งสามด้านล่างนี้ ค่า t-Statistic จะถูกคํานวณและแสดงเป็น "t Stat" ในตารางผลลัพธ์ ค่า t นี้อาจเป็นค่าลบหรือไม่เป็นลบ ทั้งนี้ขึ้นอยู่กับข้อมูล ภายใต้ข้อสมมติฐานของประชากรที่เป็นฐานเท่ากับหมายถึง ถ้า t < 0, "P(T <= t) one-tail" จะให้ความน่าจะเป็นที่ค่าของสถิติ t จะสังเกตเห็นว่ามีค่าลบมากกว่า t ถ้า t >=0, "P(T <= t) one-tail" จะทําให้ความน่าจะเป็นที่ค่าของ t-Statistic จะถูกสังเกตว่ามีค่าบวกมากกว่า t "t Critical one-tail" ให้ค่าตัด เพื่อให้ความน่าจะเป็นของการสังเกตค่าของ t-Statistic มากกว่าหรือเท่ากับ "t Critical one-tail" คือ Alpha
"P(T <= t) two-tail" จะให้ความน่าจะเป็นที่ค่าของ t-Statistic จะสังเกตเห็นว่ามีขนาดใหญ่กว่าค่าสัมบูรณ์มากกว่า t "P Critical two-tail" ให้ค่าตัด เพื่อให้ความน่าจะเป็นของ t-Statistic ที่สังเกตมีขนาดใหญ่กว่าค่าสัมบูรณ์มากกว่า "P Critical two-tail" คือ Alpha
t-Test: จับคู่สองตัวอย่างสำหรับค่าเฉลี่ย
คุณสามารถใช้การทดสอบจับคู่เมื่อมีการจับคู่ค่าสังเกตอย่างเป็นธรรมชาติในตัวอย่าง เช่น เมื่อทดสอบกลุ่มตัวอย่างสองครั้ง ก่อนและหลังการทดลอง เครื่องมือการวิเคราะห์นี้และสูตรของนักเรียนดําเนินการจับคู่สองตัวอย่าง t-Test เพื่อตรวจสอบว่าข้อสังเกตที่นํามาก่อนการรักษาและการสังเกตที่เกิดขึ้นหลังจากการรักษามีแนวโน้มที่จะมาจากการกระจายที่มีค่าเฉลี่ยประชากรเท่ากันหรือไม่ ฟอร์ม t-Test นี้ไม่ถือว่าค่าความแปรปรวนของประชากรทั้งสองเท่ากัน
หมายเหตุ: ในบรรดาผลลัพธ์ที่สร้างโดยเครื่องมือนี้คือค่าความแปรปรวนรวม ซึ่งเป็นการวัดสะสมของข้อมูลที่กระจายค่าอยู่รอบค่าเฉลี่ย และสามารถหาได้จากสูตรต่อไปนี้
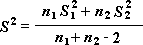
t-Test: สองตัวอย่างที่ตั้งสมมติฐานว่าความแปรปรวนเท่ากัน
เครื่องมือการวิเคราะห์นี้จะทําการทดสอบ t-Test ของนักเรียนสองตัวอย่าง แบบฟอร์ม t-Test นี้จะถือว่าชุดข้อมูลทั้งสองชุดมาจากการแจกแจงที่มีค่าความแปรปรวนเหมือนกัน เรียกว่าเป็น homoscedastic t-Test คุณสามารถใช้ t-Test นี้เพื่อตรวจสอบว่าตัวอย่างทั้งสองนี้น่าจะมาจากการแจกแจงที่มีค่าเฉลี่ยประชากรเท่ากันหรือไม่
t-Test: สองตัวอย่างที่ตั้งสมมติฐานว่าความแปรปรวนไม่เท่ากัน
เครื่องมือการวิเคราะห์นี้จะทําการทดสอบ t-Test ของนักเรียนสองตัวอย่าง แบบฟอร์ม t-Test นี้จะถือว่าชุดข้อมูลทั้งสองชุดมาจากการแจกแจงที่มีค่าความแปรปรวนที่ไม่เท่ากัน เรียกว่าเป็นการทดสอบแบบ tteroscedastic เช่นเดียวกับตัวพิมพ์ค่าความแปรปรวนที่เท่ากันก่อนหน้า คุณสามารถใช้ t-Test นี้เพื่อกําหนดว่าตัวอย่างทั้งสองนี้น่าจะมาจากการแจกแจงที่มีค่าเฉลี่ยประชากรเท่ากันหรือไม่ ใช้การทดสอบนี้เมื่อมีวิชาที่แตกต่างกันในสองตัวอย่าง ใช้การทดสอบจับคู่ ตามที่อธิบายไว้ในตัวอย่างต่อไปนี้ เมื่อมีหัวข้อชุดเดียว และตัวอย่างสองชุดแสดงการวัดสําหรับแต่ละหัวข้อก่อนและหลังการรักษา
สูตรต่อไปนี้จะใช้กำหนดค่าสถิติ t
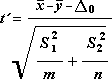
สูตรต่อไปนี้จะใช้ในการคํานวณระดับความเป็นอิสระ df เนื่องจากผลลัพธ์ของการคํานวณมักจะไม่ใช่จํานวนเต็ม ค่าของ df จะถูกปัดเศษให้เป็นจํานวนเต็มที่ใกล้เคียงที่สุดเพื่อรับค่าวิกฤตจากตาราง t ฟังก์ชันเวิร์กชีต Excel TTEST จะใช้ค่า df ที่คํานวณโดยไม่มีการปัดเศษ เนื่องจากเป็นไปได้ที่จะคํานวณค่า Tทดสอบ กับค่า df ที่ไม่ใช่จํานวนเต็ม เนื่องจากวิธีการที่แตกต่างกันเหล่านี้เพื่อกําหนดระดับความเป็นอิสระผลลัพธ์ของ TTEST และเครื่องมือ t-Test นี้จะแตกต่างกันในกรณีค่าความแปรปรวนที่ไม่เท่ากัน
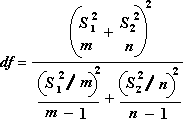
z-Test: เครื่องมือการวิเคราะห์สองตัวอย่างสําหรับค่าเฉลี่ยจะดําเนินการ z-Test สองตัวอย่างสําหรับค่าเฉลี่ยที่มีค่าความแปรปรวนที่ทราบแล้ว เครื่องมือนี้ใช้เพื่อทดสอบสมมติฐานว่าไม่มีความแตกต่างระหว่างประชากรสองวิธีเทียบกับสมมติฐานทางเลือกด้านเดียวหรือสองด้าน ถ้าไม่ทราบค่าความแปรปรวน ฟังก์ชันเวิร์กชีต Zควรใช้การทดสอบแทน
เมื่อคุณใช้เครื่องมือ z-Test โปรดระวังเพื่อทําความเข้าใจผลลัพธ์ "P(Z <= z) one-tail" คือ P(Z >= ABS(z)) ความน่าจะเป็นของค่า z ที่อยู่ไกลจาก 0 ในทิศทางเดียวกับค่า z ที่สังเกตได้เมื่อไม่มีความแตกต่างระหว่างวิธีของประชากร "P(Z <= z) two-tail" คือ P(Z >= ABS(z) หรือ Z <= -ABS(z)) ความน่าจะเป็นของค่า z ที่อยู่ไกลจาก 0 ในทิศทางใดทิศทางหนึ่งมากกว่าค่า z ที่สังเกตได้เมื่อไม่มีความแตกต่างระหว่างค่าเฉลี่ยประชากร ผลลัพธ์แบบสองด้านเป็นเพียงผลลัพธ์ด้านเดียวที่คูณด้วย 2 เครื่องมือ z-Test ยังสามารถใช้สําหรับกรณีที่สมมติฐาน Null คือมีค่าที่ไม่ใช่ศูนย์ที่เฉพาะเจาะจงสําหรับความแตกต่างระหว่างค่าเฉลี่ยของประชากรทั้งสอง ตัวอย่างเช่น คุณสามารถใช้การทดสอบนี้เพื่อกําหนดความแตกต่างระหว่างการแสดงของรถยนต์สองรุ่น
ต้องการความช่วยเหลือเพิ่มเติมไหม
คุณสามารถสอบถามผู้เชี่ยวชาญใน Excel Tech Community หรือรับการสนับสนุนใน ชุมชน
ดูเพิ่มเติม
สร้างแผนภูมิ Pareto ใน Excel 2016
โหลด Analysis ToolPak ใน Excel
ฟังก์ชันวิศวกรรม (ข้อมูลอ้างอิง)
วิธีการหลีกเลี่ยงสูตรที่ใช้งานไม่ได้
แป้นพิมพ์ลัดและแป้นฟังก์ชัน Excel










