Komplex adatelemzés az Analysis ToolPak bővítménnyel

1. Kattintson a Fájl lap Beállítások gombjára, majd a Bővítmények kategóriára.

2. A Kezelés legördülő listában válassza az Excel-bővítmények lehetőséget, és kattintson az Ugrás gombra.

   Mac Excel használata esetén a Fájl menüben keresse meg az Eszközök > Excel-bővítmények parancsot.

3. Jelölje be a Bővítmények párbeszédpanelen az Analysis ToolPak jelölőnégyzetet, és kattintson az OK gombra.

   • Ha az Analysis ToolPak nem szerepel a Létező bővítmények listában, akkor a Tallózás gombra kattintva megkeresheti.

   • Ha az alkalmazás kiírja, hogy az Analysis ToolPak bővítmény nincs a számítógépen telepítve, akkor a telepítéshez kattintson az Igen gombra.

Az Anova (Analysis of Variance) elemzőeszközzel különféle típusú varianciaanalízisek végezhetők. A választandó eszközt a tényezők száma, illetve a statisztikai sokaságból vett és a próbának alávetni kívánt minták száma határozza meg.

Egytényezős varianciaanalízis

Ez az eszköz egyszerű elemzést végez két vagy több minta adatainak varianciájáról. Az elemzés azt a hipotézist teszteli, hogy az egyes mintákat ugyanabból a mögöttes valószínűségi eloszlásból, az alternatív hipotézissel összevetve, hogy a mögöttes valószínűségeloszlások nem azonosak az összes mintára vonatkozóan. Ha csak két minta létezik, használhatja a T munkalapfüggvényt.TESZT. Kétnál több mintával a T-nek nincs kényelmes általánosítása.A TEST és a Single Factor Anova modell hívható meg helyette.

Kéttényezős varianciaanalízis ismétlésekkel

Ez az elemzőeszköz akkor hasznos, ha az adatok két különböző dimenzió szerint osztályozhatók. Adott például egy kísérlet, amelyben a növények magasságát mérik, miközben különféle márkájú tápoldatokkal (például A, B, C) kezelik, ezenkívül különböző hőmérsékletnek (alacsony, magas) is teszik ki őket. A hat lehetséges {tápoldat, hőmérséklet} párosítás mindegyikéhez egyenlő számú magasságmérés tartozik. Ekkor varianciaanalízissel vizsgálhatók a következők:

• A különböző tápoldatmárkához tartozó növénymagasságok ugyanabból a sokaságból származnak-e. Ez az elemzés nem veszi figyelembe a hőmérséklet hatását.

• A különböző hőmérsékletekhez tartozó növénymagasságok ugyanabból a sokaságból származnak-e. Ebben az esetben a tápoldatok hatását hagyja figyelmen kívül.

Figyelembe véve az első pontban a tápoldatmárkák között észlelt különbségeket, valamint a második pontban a hőmérsékletek között észlelt különbségeket, az összes {tápoldat, hőmérséklet} értékpárt képviselő hat minta ugyanabból a sokaságból származik-e. Az alternatív hipotézis szerint amellett, hogy a hőmérséklet vagy a tápoldat változása külön-külön eltérést okoz, az egyes {tápoldat, hőmérséklet} pároknak további hatás is tulajdonítható.

Kéttényezős varianciaanalízis ismétlések nélkül

Ez az elemzőeszköz akkor használható, ha az adatok két különböző dimenzió szerint osztályozhatók, a kéttényezős, ismétléses varianciaanalízishez hasonlóan. Itt azonban feltételezzük, hogy minden párhoz (például az előző példában minden {tápoldat, hőmérséklet} párhoz) csak egy megfigyelés tartozik.

A KORREL és a PEARSON munkalapfüggvény egyaránt két mérési változó korrelációs együtthatóját számítja ki olyan mérések alapján, amelyek során mindegyik változót n egyeden mértek meg. (Ha bármelyik egyed esetében hiányzik valamelyik mérés, akkor az az egyed kimarad az elemzésből). A korrelációanalízis különösen hasznos, ha az n egyed mindegyikéhez kettőnél több mérési változó tartozik. Az eszköz egy táblázatban – a korrelációs mátrixban – megjeleníti a KORREL (vagy PEARSON) értéket az összes lehetséges értékpárra.

A korrelációs együttható, mint a kovariancia, azt méri, hogy a két mérési változó milyen mértékben "változik együtt". A kovarianciával ellentétben a korrelációs együttható úgy van skálázva, hogy az értéke független legyen a két mérési változó mértékegységétől. (Ha például a két mérési változó a súly és a magasság, a korrelációs együttható értéke változatlan marad, ha a súlyt fontról kilogrammra konvertálják.) Bármely korrelációs együttható értékének -1 és +1 közöttinek kell lennie.

Ha a korrelációanalízissel megvizsgálja az összes értékpárt, meghatározhatja, hogy a két mérési változó együtt mozog-e, vagyis az egyik változó nagyobb értékei a másik változó értékének növekedésével vannak-e összefüggésben (pozitív korreláció), vagy éppen fordítva, az egyik változó nagyobb értékeihez a másik változó kisebb értékei tartoznak (negatív korreláció), vagy a két változó értékei között nem fedezhető fel kapcsolat (a korreláció nullához közeli).

A korrelációs és a kovarianciai eszközök is használhatók ugyanabban a beállításban, ha N különböző mérési változók figyelhetők meg egyedek halmazán. A Korreláció és a Kovariancia eszközök mindegyike egy kimeneti táblát, egy mátrixot ad, amely a korrelációs együtthatót vagy a kovarianciát mutatja az egyes mérési változópárok között. A különbség az, hogy a korrelációs együtthatók a -1 és +1 közötti értékre vannak skálázva. A megfelelő kovarianciák nincsenek skálázva. A korrelációs együttható és a kovariancia is annak mértéke, hogy a két változó milyen mértékben "változik együtt".

A Kovariancia eszköz kiszámítja a munkalapfüggvény KOVARIANCIA értékét. P minden mérési változópárhoz. (A KOVARIANCIA közvetlen használata. A Kovariancia eszköz helyett a P ésszerű alternatíva, ha csak két mérési változó van, azaz N=2.) A Kovariancia eszköz kimeneti táblázatának i. sorában az i. oszlopban lévő átlós bejegyzés az i-edik mérési változó kovarianciája önmagával. Ez csak a változó sokasági varianciája, amelyet a VAR munkalapfüggvény számít ki.P.

Ha a varianciaanalízissel megvizsgálja az összes értékpárt, meghatározhatja, hogy a két mérési változó együtt mozog-e, vagyis az egyik változó nagyobb értékei a másik változó értékének növekedésével vannak-e összefüggésben (pozitív kovariancia), vagy éppen fordítva, az egyik változó nagyobb értékeihez a másik változó kisebb értékei tartoznak (negatív kovariancia), vagy a két változó értékei között nem fedezhető fel kapcsolat (a kovariancia nullához közeli).

A leíró statisztika elemzőeszköz egyváltozós statisztikai jelentést készít a kiindulási adattartományról, és információt nyújt az adatok súlypontjáról és változatosságáról.

Az exponenciális simítással a korábbi időszak adatai alapján előre lehet jelezni egy, az előző időszak hibaértékeivel korrigált értéket. A módszer az a simítási állandót használja, ennek nagysága határozza meg, hogy a megelőző időszakból származó hibák mekkora hatást gyakoroljanak az előrejelzésekre.

A kétmintás f-próba két statisztikai sokaság szórásnégyzetét hasonlítja össze.

Használhatja például az F-Test eszközt az úszó értekezleteken való időmintákon, mindkét csapat számára. Az eszköz azt a nullhipotézist teszteli, hogy ez a két minta egyenlő varianciával rendelkező eloszlásokból származik, azzal az alternatívával, hogy a varianciák nem egyenlők az alapul szolgáló eloszlásokban.

Az eszköz egy F-statisztika (vagy F viszonyszám) f értékét számolja ki. Az 1-hez közeli f érték azt bizonyítja, hogy a vizsgált sokasági varianciák megegyeznek. Ha az eredménytáblában f < 1, akkor a „P(F <= f) egyoldalú próba” annak a valószínűségét jelenti, hogy az F-statisztika megfigyelt értéke kisebb, mint f, amennyiben a sokasági varianciák egyenlőek, és az „F-kritikus egyoldalú próba” kritikus értéke 1-nél kisebb a választott alfa pontossági szinthez. Ha f > 1, akkor a „P(F >= f) egyoldalú próba” annak a valószínűségét jelenti, hogy az F-statisztika megfigyelt értéke nagyobb, mint f, amennyiben a sokasági varianciák egyenlőek, és az „F-kritikus egyoldalú próba” kritikus értéke 1-nél nagyobb a választott alfa szinthez.

Lineáris rendszerek és periodikus adatok elemzésére használható, az adatokat a gyors Fourier-transzformáció (Fast Fourier Transform - FFT) módszerével transzformálja. A művelet segítségével inverz transzformáció is végezhető, amely a transzformált adatokból visszaadja az eredeti adatokat.

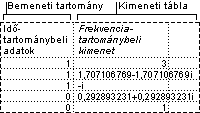
Egy cellatartomány adatai és az adatkategóriák alapján egyenkénti és halmozott gyakoriságok számíthatók ki. Az eljárással meg lehet határozni, hogy egy adott érték hányszor fordul elő az adathalmazban.

Egy 20 fős osztályban például meghatározhatja a pontszámok eloszlását betűosztályos kategóriában. A hisztogramtáblák a betűosztályos határokat, valamint a legalacsonyabb és az aktuális határérték közötti pontszámok számát jelenítik meg. Az egyetlen leggyakoribb pontszám az adatok módja.

Ez az eljárás a becsült időszak értékeit úgy számítja ki, hogy a megelőző időszak adatait megadott számú periódusonként átlagolja. A mozgó átlagolás módszerével olyan részletek derülhetnek ki a trendről, amelyek a meglévő adatok egyszerű átlagolásával elmosódnak. Ez a módszer értékesítési adatok, raktárkészletadatok vagy egyéb változó adatok előrejelzésére használható. A becsült értékeket az alábbi képlet alapján számítja ki:

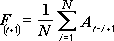
ahol:

• N a mozgó átlag periódusainak száma

• A j a tényleges érték a j időpontban

• F j a becsült érték a j időpontban

Ezzel a módszerrel több eloszlásból származó és egymástól független véletlen számokkal tölthető fel egy tartomány. Egyik alkalmazása egy sokaság egyedeinek jellemzése valószínűségi eloszlás segítségével. Például egy populáció egyedeinek magassága normális eloszlással írható le, egy két lehetséges kimenetelű esemény – ilyen a pénzfeldobás – bekövetkezésének valószínűsége pedig a Bernoulli-eloszlással jellemezhető.

A Rang és a Percentilis elemzési eszköz létrehoz egy táblát, amely egy adathalmaz egyes értékeinek sorszámát és százalékos rangját tartalmazza. Elemezheti egy adathalmaz értékeinek relatív állóhelyét. Ez az eszköz a RANK munkalapfüggvényeket használja . EQ ésPERCENTRANK. INC. Ha a kötött értékeket szeretné figyelembe venni, használja a RANK függvényt. EQ függvény, amely a kötött értékeket azonos rangúként kezeli, vagy a RANK függvényt használja .AVG függvény, amely a holt értékek átlagrangját adja vissza.

Ez az eljárás lineáris regresszióanalízist végez: a legkisebb négyzetek módszerével egyenest illeszt az adatpontok halmazára. Segítségével elemezheti, hogy egy függő változó értékét hogyan befolyásolja több független változó értéke. Megvizsgálható például, hogy egy atléta teljesítményét hogyan befolyásolják az olyan adatok, mint a kora, a magassága és a testsúlya. A teljesítményadatok alapján meghatározható, hogy az egyes tényezők milyen mértékben befolyásolják az eredményt, majd ezek alapján előre jelezhető egy új, még nem vizsgált sportoló teljesítménye.

A regressziós eszköz a LIN.VONAL munkalapfüggvényt használja.

Ez az eljárás a kiindulási adathalmazt alapsokaságnak tekinti, és abból egy mintát választ ki. A sokaságot képviselő mintát akkor használhatja, ha a teljes sokaság túl nagy a vizsgálathoz vagy az ábrázoláshoz. Ha úgy véli, hogy a kiindulási adatok periodikusak, az adatok egyetlen meghatározott ciklusából is mintát tud venni. Ha például a kiindulási tartomány értékesítési adatokat tartalmaz negyedéves bontásban, akkor a teljes időszak minden negyedik adatának kiválasztásával megkaphatja az egy adott negyedévre vonatkozó eredményeket.

A kétmintás t-próba eszközeivel megvizsgálhatja, hogy a két sokaságnak, amelyekből a mintát vette, egyenlő-e a várható értéke. A három eszköz különböző feltételezésekből indul ki: a sokasági varianciák egyenlőek, a sokasági varianciák különbözőek, illetve a két minta olyan mérésekből áll, amelyek ugyanazon egyedek kezelés előtti és kezelés utáni állapotát tükrözik.

Mindhárom eszköz egy t-statisztika értékét, t-t számítja ki és jeleníti meg t-statisztika néven az eredménytáblákban. Az adatoktól függően ez a t érték lehet negatív vagy nem negatív. Feltéve, hogy a vizsgált sokaságok várható értékei egyenlőek, ha t < 0, akkor a „P(T <= t) egyoldalú próba” annak a valószínűségét jelenti, hogy a t-statisztika vizsgált értéke egy t-nél kisebb negatív érték. Ha t >=0, a „P(T >= t) egyoldalú próba” annak a valószínűségét jelenti, hogy a t-statisztika vizsgált értéke egy t-nél nagyobb pozitív érték. A „t-kritikus egyoldalú próba” a szakadási pont értékét adja meg, így annak a valószínűsége, hogy a t-statisztika vizsgált értéke a „t-kritikus egyoldalú próba” értékénél nagyobb vagy egyenlő, éppen alfa.

A „P(T <= t) kétoldalú próba” annak a valószínűségét jelenti, hogy a t-statisztika vizsgált értékének abszolút értéke nagyobb t-nél. A „P-kritikus kétoldalú próba” a szakadási pont értékét adja meg, így annak a valószínűsége, hogy a t-statisztika vizsgált értékének abszolút értéke a „P-kritikus kétoldalú próba” értékénél nagyobb, éppen alfa.

Kétmintás párosított t-próba a várható értékre

Párosított tesztet akkor használhat, ha a mintákban természetes megfigyeléspárok vannak, például ha egy mintacsoportot kétszer tesztelnek – egy kísérlet előtt és után. Ez az elemzőeszköz és képlete párosított kétmintás Student's t-Test tesztet hajt végre annak megállapításához, hogy a kezelés előtt elvégzett megfigyelések és a kezelés utáni megfigyelések valószínűleg azonos sokasági középértékkel rendelkező eloszlásokból származnak-e. Ez a t-test űrlap nem feltételezi, hogy mindkét sokaság varianciája egyenlő.

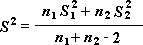
Kétmintás t-próba egyenlő szórásnégyzeteknél

Ez az elemzőeszköz egy kétmintás tanuló t-tesztjét hajtja végre. Ez a t-test űrlap feltételezi, hogy a két adathalmaz azonos varianciájú eloszlásokból származik. Homoscedasztikus t-testnek nevezzük. Ezzel a t-teszttel megállapíthatja, hogy a két minta valószínűleg egyenlő sokaságú eloszlásokból származik-e.

Kétmintás t-próba nem egyenlő szórásnégyzeteknél

Ez az elemzőeszköz egy kétmintás tanuló t-tesztjét hajtja végre. Ez a t-test űrlap feltételezi, hogy a két adathalmaz egyenlőtlen varianciájú eloszlásokból származik. Heteroscedastic t-Test-nek nevezzük. A fenti Egyenlő varianciák esethez hasonlóan ezzel a t-próbával megállapíthatja, hogy a két minta valószínűleg egyenlő sokasági középértékkel rendelkező eloszlásokból származik-e. Akkor használja ezt a tesztet, ha a két mintában különböző alanyok szerepelnek. Használja a következő példában leírt párosított tesztet, ha egyetlen alanykészlet van, és a két minta a kezelés előtt és után minden egyes témához tartozó méréseket jelöl.

A t statisztikai érték az alábbi képlettel számítható ki.

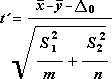
Az alábbi képlet a szabadságfokok (df) kiszámítására szolgál. Mivel a számítás eredménye általában nem egész szám, a df értékét a függvény a legközelebbi egész számra kerekíti, hogy kritikus értéket kapjon a t táblából. Az Excel munkalap T függvénye.A TEST a számított df értéket használja kerekítés nélkül, mivel a T értékének kiszámítása lehetséges.TEST egy nem egész szám df-el. A szabadságfok meghatározásának különböző megközelítései miatt a T eredménye.A TEST és a t-Test eszköz eltérő lesz az Egyenlőtlen varianciák esetében.

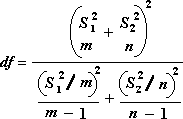
A z-Test: Two Sample for Means elemző eszköz két z-próbát végez az ismert varianciájú eszközökhöz. Ez az eszköz annak a nullhipotézisnek a tesztelésére szolgál, hogy nincs különbség a két sokaság középértékei és az egyoldalas vagy kétoldalas alternatív hipotézisek között. Ha a varianciák nem ismertek, a munkalap Z függvénye.Ehelyett a TEST függvényt kell használni.

A z-próba használatakor fontos, hogy jól értelmezze az eredményt. A „P(Z <= z) egyoldalú próba” valójában a P(Z >= ABS(z)), vagyis annak a z értéknek a valószínűsége, amely a 0-tól távolabb, ugyanabban az irányban van, mint a vizsgált z érték, és a sokaság várható értékei között nincs eltérés. A „P(Z <= z) kétoldalú próba” valójában a P(Z >= ABS(z) vagy a Z <= -ABS(z)), vagyis annak a z értéknek a valószínűsége, amely a 0-tól bármely irányban távolabb van a vizsgált z értéknél, és a sokaság várható értékei között nincs eltérés. A kétoldalú próba eredménye az egyoldalú próba eredményének a kétszerese. A z-próba akkor is használható, ha a nullhipotézis az, hogy a két sokaság várható értékeinek különbsége egy adott, nullától különböző érték. A módszer alkalmas lehet például két autómodell teljesítménykülönbségének vizsgálatára.