Menggunakan Analysis ToolPak untuk menjalankan analisis data kompleks

1. Klik tab File, klik Opsi, lalu klik kategori Add-In.

2. Di kotak Kelola, klik Add-in Excel, lalu klik Jalankan.

   Jika Anda menggunakan Excel untuk Mac, dalam menu file, masuk ke Alat > Add-in Excel.

3. Dalam kotak Add-In , centang kotak Analysis ToolPak , lalu klik OK.

   • Jika Analysis ToolPak tidak terdaftar dalam kotak Add-In yang tersedia, klik Telusuri untuk menemukannya.

   • Jika Anda diberi tahu bahwa Analysis ToolPak tidak terinstal di komputer Anda, klik Ya untuk menginstalnya.

Alat analisis Anova menyediakan berbagai tipe analisis variansi. Alat yang harus Anda gunakan tergantung jumlah faktor dan jumlah sampel yang Anda miliki dari populasi yang ingin diuji.

Anova: Faktor Tunggal

Alat ini melakukan analisis sederhana varians data untuk dua sampel atau lebih. Analisis ini memberikan uji hipotesis bahwa setiap sampel diambil dari distribusi probabilitas yang mendasar yang sama terhadap hipotesis alternatif bahwa distribusi probabilitas yang mendasar tidak sama untuk semua sampel. Jika hanya ada dua sampel, Anda bisa menggunakan fungsi lembar kerja T.TES. Dengan lebih dari dua sampel, tidak ada generalisasi T yang nyaman.TEST, dan model Anova Faktor Tunggal dapat dipanggil sebagai gantinya.

Anova: Dua-Faktor dengan Replikasi

Alat analisis ini bermanfaat saat data dapat diklasifikasi dalam dua dimensi yang berbeda. Contohnya, dalam eksperimen untuk mengukur tinggi tanaman, tanaman dapat diberi merek pupuk yang berbeda (misalnya, A, B, C) dan juga dapat disimpan pada suhu yang berbeda (misalnya, rendah, tinggi). Untuk setiap kemungkinan pasangan dari total enam pasangan {pupuk, suhu}, kita memiliki jumlah pengamatan tinggi tanaman yang sama. Dengan alat Anova ini, kita dapat menguji:

• Apakah tinggi tanaman untuk merek pupuk yang berbeda diambil dari populasi dasar yang sama. Suhu diabaikan pada analisis ini.

• Apakah tinggi tanaman untuk tingkat suhu yang berbeda diambil dari populasi dasar yang sama. Merek pupuk diabaikan pada analisis ini.

Apakah setelah mempertimbangkan efek perbedaan antara merek pupuk yang ditemukan pada poin bullet pertama dan perbedaan suhu yang ditemukan pada poin bullet kedua, keenam sampel menunjukkan semua pasangan nilai {pupuk, suhu} diambil dari populasi yang sama. Hipotesis alternatif yaitu terdapat efek akibat pasangan {pupuk, suhu} tertentu pada perbedaan yang berdasarkan pupuk saja atau suhu saja.

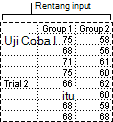
Anova: Dua-Faktor Tanpa Replikasi

Alat analisis ini bermanfaat saat data diklasifikasikan berdasarkan dua dimensi yang berbeda seperti pada kasus Dua-Faktor Dengan Replikasi. Namun, untuk alat ini diasumsikan bahwa hanya ada satu pengamatan untuk setiap pasangan (misalnya, setiap pasangan {pupuk, suhu} dalam contoh sebelumnya).

Fungsi lembar kerja CORREL dan PEARSON sama-sama menghitung koefisien korelasi antara dua variabel pengukuran ketika pengukuran pada setiap variabel diamati untuk setiap subjek N. (Pengamatan apa pun yang hilang untuk setiap penyebab subjek yang harus diabaikan dalam analisis.) Alat analisis Korelasi sangat berguna ketika terdapat lebih dari dua variabel pengukuran untuk setiap subjek N. Ini menyediakan tabel output, matriks korlasi, yang memperlihatkan nilai CORREL (atau PEARSON) yang diterapkan ke setiap pasangan variabel pengukuran yang mungkin.

Koefisien korlasi, seperti kovarians, adalah ukuran sejauh mana dua variabel pengukuran "bervariasi bersama-sama." Tidak seperti kovarians, koefisien korlasi diskalakan sehingga nilainya terpisah dari satuan di mana dua variabel pengukuran dinyatakan. (Misalnya, jika dua variabel pengukuran adalah berat dan tinggi, nilai koefisien korelasi tidak berubah jika berat dikonversi dari pon menjadi kilogram.) Nilai koefisien korlasi apa pun harus antara -1 dan +1 inklusif.

Anda dapat menggunakan alat analisis korelasi untuk memeriksa setiap pasangan variabel pengukuran untuk menentukan apakah dua variabel pengukuran cenderung bergerak bersama — yaitu, apakah nilai yang lebih besar pada satu variabel cenderung terkait dengan nilai yang lebih besar pada variabel lain (korelasi positif), apakah nilai yang lebih kecil pada satu variabel cenderung terkait dengan nilai yang lebih besar pada variabel lain (korelasi negatif), atau apakah nilai kedua variabel cenderung tidak terkait (korelasi mendekati 0 (nol)).

Alat Korelasi dan Kovariansi dapat digunakan dalam pengaturan yang sama, saat Anda memiliki N variabel pengukuran yang berbeda yang diamati pada sekumpulan individu. Alat Korelasi dan Kovariansi memberi tabel output, matriks, yang menunjukkan koefisien atau kovariansi korelasi, secara berurutan, antar tiap pasang variabel pengukuran. Perbedaannya adalah bahwa koefisien korelasi diskalakan antara serta mencakup -1 dan +1. Kovariansi terkait tidak diskalakan. Koefisien dan kovariansi korelasi adalah ukuran rentang kedua variabel "bergerak bersama."

Alat Kovarians menghitung nilai fungsi lembar kerja COVARIANCE. P untuk setiap pasang variabel pengukuran. (Penggunaan langsung COVARIANCE. P daripada alat Kovarians adalah alternatif yang masuk akal ketika hanya ada dua variabel pengukuran, yaitu, N=2.) Entri pada diagonal tabel output alat Kovarians di baris i, kolom i adalah kovarians variabel pengukuran ke-i dengan sendirinya. Ini hanya varians populasi untuk variabel tersebut, seperti yang dihitung oleh fungsi lembar kerja VAR.P.

Anda dapat menggunakan alat Kovariansi untuk memeriksa setiap pasangan variabel pengukuran untuk menentukan apakah dua variabel pengukuran cenderung bergerak bersama — yaitu, apakah nilai yang lebih besar pada satu variabel cenderung terkait dengan nilai yang lebih besar pada variabel lain (kovariansi positif), apakah nilai yang lebih kecil pada satu variabel cenderung terkait dengan nilai yang lebih besar pada variabel lain (kovariansi negatif), atau apakah nilai kedua variabel cenderung tidak terkait (korelasi mendekati 0 (nol)).

Alat analisis Statistik Deskriptif menghasilkan laporan statistik univariat untuk data dalam rentang input, menyediakan informasi tentang kecenderungan dan variabilitas utama data.

Alat analisis Pemulusan Eksponensial memprediksikan nilai yang berdasarkan perkiraan periode sebelumnya, yang disesuaikan berdasarkan kesalahan dalam perkiraan sebelumnya. Alat ini menggunakan konstan pemulusan a, yang besarnya menentukan kekuatan perkiraan merespons kesalahan dalam perkiraan sebelumnya.

Alat analisis Uji-F Dua Sampel untuk Variansi menjalankan uji-F dua sampel untuk membandingkan dua variansi populasi.

Contohnya, Anda dapat menggunakan alat uji-F pada sampel jumlah waktu dalam sekali renang yang dicapai masing-masing dari dua tim. Alat ini memberikan hasil tes hipotesis null bahwa kedua sampel ini berasal dari distribusi dengan variansi yang sama, dibandingkan dengan alternatif bahwa variansi tidak sama dalam distribusi yang mendasari.

Alat ini menghitung nilai f dari sebuah statistik-F (atau rasio-F). Sebuah nilai f yang mendekati 1 memberi bukti bahwa variansi populasi yang mendasari sama. Dalam tabel output, jika f < 1 "P(F <= f) satu-sisi" memberi probabilitas mengamati nilai statistik-F kurang dari f saat variansi populasi sama, dan "Nilai kritis F satu-sisi" memberi nilai kritis kurang dari 1 untuk tingkat signifikansi terpilih, Alpha. Jika f > 1, "P(F <= f) satu sisi" memberi probabilitas mengamati nilai statistik-F lebih besar dari f saat variansi populasi sama, dan "Nilai kritis F satu-sisi" memberi nilai kritis lebih besar dari 1 untuk Alpha.

Alat Analisis Fourier memecahkan masalah dalam sistem linear dan menganalisis data periodik menggunakan metode Fast Fourier Transform (FFT) untuk mentransformasi data. Alat ini juga mendukung transformasi inversi, di mana inversi data yang ditransformasi mengembalikan data asli.

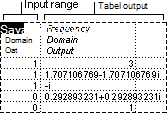
Alat analisis Histogram menghitung frekuensi tunggal dan kumulatif untuk rentang sel data dan keranjang data. Alat ini menghasilkan data untuk jumlah kemunculan nilai dalam set data.

Contohnya, dalam kelas berisi 20 siswa, Anda dapat menentukan distribusi skor dalam kategori peringkat huruf. Sebuah tabel histogram menyajikan batas peringkat huruf dan jumlah skor antara batas terendah dan batas terkini. Skor tunggal yang paling sering muncul disebut mode data.

Alat analisis Rata-rata Bergerak memproyeksi nilai dalam periode perkiraan, berdasarkan nilai rata-rata variabel atas angka spesifik dari periode sebelumnya. Rata-rata bergerak menyediakan informasi tren yang akan dicakup rata-rata sederhana dari semua data riwayat. Gunakan alat ini untuk memperkirakan penjualan, inventaris, atau tren lain. Setiap nilai perkiraan didasarkan pada rumus berikut.

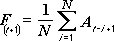
di mana:

• N adalah jumlah periode sebelumnya yang dicakup dalam rata-rata bergerak

• A j adalah nilai aktual saat ini j

• F j nilai perkiraan saat ini j

Alat analisis Pembuatan Angka Acak mengisi sebuah rentang dengan angka acak independen yang diperoleh dari salah satu distribusi. Anda dapat mengkarakterisasi subjek dalam populasi dengan distribusi probabilitas. Contohnya, Anda dapat menggunakan distribusi normal untuk mengkarakterisasi populasi berdasarkan tinggi badan individu, atau Anda dapat menggunakan distribusi Bernoulli dari dua hasil yang mungkin untuk mengkarakterisasi populasi berdasarkan hasil undian mata uang.

Alat analisis Peringkat dan Persentil menghasilkan tabel yang berisi peringkat ordinal dan persentase dari setiap nilai dalam kumpulan data. Anda bisa menganalisis posisi relatif nilai dalam rangkaian data. Alat ini menggunakan fungsi lembar kerja RANK. EQ danPERCENTRANK. INC. Jika Anda ingin memperhitungkan nilai yang diikat, gunakan RANK. Fungsi EQ , yang memperlakukan nilai terikat sebagai memiliki peringkat yang sama, atau menggunakan RANK.Fungsi AVG , yang mengembalikan peringkat rata-rata untuk nilai yang diikat.

Alat analisis Regresi menjalankan analisis regresi linear menggunakan metode "kuadrat terkecil" agar pas dalam serangkaian pengamatan. Anda dapat menganalisis pengaruh nilai satu atau beberapa variabel independen pada variabel dependen tunggal. Contohnya, Anda dapat menganalisis pengaruh faktor seperti usia, tinggi, dan berat badan pada performa atlet. Anda dapat menugaskan bagian dalam pengukuran performa ke setiap faktor, berdasarkan set data performa, lalu gunakan hasil untuk memprediksi performa atlet baru yang belum teruji.

Alat Regresi menggunakan fungsi lembar kerja LINEST.

Alat analisis Sampling membuat sampel dari populasi dengan memperlakukan rentang input sebagai populasi. Jika populasi terlalu besar untuk diproses atau dibuat bagan, Anda dapat menggunakan sample representatif. Anda juga dapat membuat sampel yang hanya berisi nilai dari satu bagian tertentu siklus jika Anda yakin bahwa data input bersifat periodik. Contohnya, jika rentang input berisi angka penjualan kuartal, sampling dengan angka periodik empat menempatkan nilai dari kuartal yang sama dalam rentang output.

Alat analisis Uji-t Dua-Sampel menguji kesamaan mean populasi yang mendasari setiap sampel. Ketiga alat menggunakan asumsi berbeda: bahwa variansi populasi sama, bahwa variansi populasi tidak sama, dan bahwa dua sampel mewakili pengamatan sebelum dan sesudah-perlakuan pada subjek yang sama.

Untuk ketiga alat di bawah, sebuah nilai Statistik-t, yaitu t, dihitung dan ditampilkan sebagai "t Stat" dalam tabel output. Tergantung data, nilai ini, t, bisa berupa negatif atau nonnegatif. Dengan asumsi mean populasi dasar yang sama, jika t < 0, "P(T <= t) satu-sisi" memberi probabilitas bahwa nilai Statistik-t yang akan diamati lebih negatif daripada t. Jika t >=0, "P(T <= t) satu-sisi" memberi probabilitas bahwa nilai Statistik-t yang akan diamati lebih positif daripada t. "Nilai kritis t satu-sisi" memberi nilai batas, sehingga probabilitas pengamatan nilai Statistik-t lebih besar dari atau sama dengan "nilai kritis t satu-sisi" yaitu Alpha.

"P(T <= t) dua-sisi" memberi probabilitas bahwa nilai Statistik-t yang akan diamati lebih besar dalam nilai absolut daripada t. "Nilai kritis P dua-sisi" memberi nilai batas, sehingga probabilitas Statistik-t yang diamati lebih besar dalam nilai absolut daripada "Nilai kritis P dua-sisi" yaitu Alpha.

Uji-t: Dua Sampel Dipasangkan Untuk Mean

Anda dapat menggunakan tes berpasangan jika terdapat pasangan alami pengamatan dalam sampel, seperti saat grup sampel diuji dua kali — sebelum dan setelah eksperimen. Alat analisis ini dan formulanya menjalankan Uji-t Siswa dua sampel berpasangan untuk menentukan apakah pengamatan sebelum perlakuan dan pengamatan setelah perlakuan cenderung berasal dari distribusi dengan mean populasi yang sama. Bentuk Uji-t tidak berasumsi bahwa variansi kedua populasi sama.

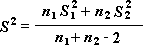
Uji-t: Dua-Sampel dengan Variansi yang Sama

Alat analisis ini menjalankan Uji-t dua sampel siswa. Bentuk Uji-t ini mengasumsikan dua set data berasal dari distribusi dengan variansi yang sama. Uji ini disebut sebagai Uji-t homoskedastik. Anda dapat menggunakan Uji-T ini untuk menentukan apakah dua sampel cenderung berasal dari distribusi dengan mean populasi yang sama.

Uji-t: Dua-Sampel dengan Variansi yang Tidak Sama

Alat analisis ini menjalankan Uji-t dua sampel siswa. Bentuk Uji-t ini mengasumsikan dua set data berasal dari distribusi dengan variansi yang tidak sama. Uji ini disebut sebagai Uji-t heteroskedastik. Seperti halnya kasus Variansi Sama sebelumnya, Anda dapat menggunakan Uji-t ini untuk menentukan apakah kedua sampel cenderung berasal dari distribusi dengan mean populasi yang sama. Gunakan uji ini jika terdapat subjek yang berlainan dalam dua sampel. Gunakan uji Berpasangan, yang dideskripsikan dalam contoh berikut, jika terdapat satu set subjek dan dua sampel mewakili pengukuran setiap subjek sebelum dan sesudah perlakuan.

Rumus berikut digunakan untuk menentukan nilai statistik t.

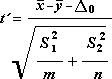
Rumus berikut digunakan untuk menghitung derajat kebebasan, df. Karena hasil perhitungan biasanya bukan bilangan bulat, nilai df dibulatkan ke bilangan bulat terdekat untuk mendapatkan nilai kritis dari tabel t. Fungsi lembar kerja Excel T.TEST menggunakan nilai df terhitung tanpa pembulatan, karena dimungkinkan untuk menghitung nilai untuk T.UJI dengan df noninteger. Karena pendekatan yang berbeda ini untuk menentukan derajat kebebasan, hasil T.TEST dan alat Uji-t ini akan berbeda dalam kasus Varians Yang Tidak Sama.

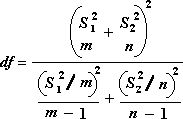
Uji-z: Alat analisis Dua Sampel untuk Berarti melakukan Uji-z dua sampel untuk sarana dengan variansi yang diketahui. Alat ini digunakan untuk menguji hipotesis null bahwa tidak ada perbedaan antara dua populasi berarti terhadap hipotesis alternatif satu sisi atau dua sisi. Jika variansi tidak diketahui, fungsi lembar kerja Z.TEST harus digunakan sebagai gantinya.

Jika Anda menggunakan alat Uji-z, berhati-hatilah dalam memahami output. "P(Z <= z) satu-sisi" benar-benar P(Z >= ABS(z)), probabilitas sebuah nilai-z menjauhi 0 dengan arah yang sama seperti nilai z yang diamati jika tidak terdapat perbedaan antar mean populasi. "P(Z <= z) dua-sisi" benar-benar P(Z >= ABS(z) or Z <= -ABS(z)), probabilitas sebuah nilai-z menjauhi 0 ke kedua arah daripada nilai-z yang diamati jika tidak terdapat perbedaan antar mean populasi. Hasil dua-sisi hanyalah hasil satu-sisi dilipatkan 2. Alat Uji-z juga dapat digunakan saat hipotesis null menyatakan bahwa ada nilai non-nol tertentu untuk selisih antara dua mean populasi. Contohnya, Anda dapat menggunakan uji ini untuk menentukan perbedaan kinerja antara dua model mobil.