LINEST (Fungsi LINEST)

Deskripsi

Fungsi LINEST menghitung statistik untuk sebuah garis dengan menggunakan metode "kuadrat terkecil" untuk menghitung garis lurus yang paling cocok dengan data Anda, dan kemudian mengembalikan array yang menguraikan garis tersebut. Anda juga dapat mengombinasikan LINEST dengan fungsi-fungsi lainnya untuk menghitung statistik untuk tipe model lain yang linear dalam parameter yang tidak diketahui, termasuk polinomial, logaritmik, eksponensial, dan serangkaian pangkat. Karena fungsi ini mengembalikan sebuah array nilai, maka harus dimasukkan sebagai rumus array. Petunjuk mengikuti contoh-contoh dalam artikel ini.

Persamaan untuk garis adalah:

y = mx + b

–atau–

y = m1x1 + m2x2 + ... + b

jika ada beberapa rentang nilai x, di mana nilai y tidak bebasnya adalah fungsi nilai x bebas. Nilai m adalah koefisien yang berkaitan dengan setia nilai x, dan b adalah nilai konstanta. Perhatikan y, x, dan m bisa menjadi vektor. Array yang dikembalikan oleh fungsi LINEST adalah {mn,mn-1,...,m1,b}. LINEST juga bisa mengembalikan regresi statistik tambahan.

Sintaks

LINEST(known_y's, [known_x's], [const], [stats])

Sintaks fungsi LINEST memiliki argumen berikut:

Sintaks

• known_y's    Diperlukan. Serangkaian nilai y yang sudah Anda ketahui dalam hubungan y = mx + b.

  • Jika rentang known_y's berada di dalam kolom tunggal, maka setiap kolom known_x's diterjemahkan sebagai variabel terpisah.

  • Jika rentang known_y's terdapat di dalam kolom tunggal, maka setiap kolom known_x's diterjemahkan sebagai variabel terpisah.

• known_x's    Opsional. Serangkaian nilai x yang mungkin sudah Anda ketahui dalam hubungan y = mx + b.

  • Rentang known_x's dapat mencakup satu atau lebih variabel. Jika hanya satu variabel yang digunakan, maka known_y's dan known_x's dapat berupa rentang berbentuk apa saja, selama memiliki dimensi yang sama. Jika lebih dari satu variabel yang digunakan, maka known_y's harus berupa vektor (yaitu, rentang dengan tinggi satu baris atau lebar satu kolom).

  • Jika known_x's dikosongkan, maka diasumsikan sebagai array {1,2,3,...} yang memiliki ukuran sama dengan known_y's.

• const    Opsional. Sebuah nilai logika yang menentukan apakah memaksakan konstanta b sama dengan 0.

  • Jika const TRUE atau dikosongkan, maka b dihitung secara normal.

  • Jika const FALSE, maka b diatur agar sama dengan 0 dan nilai m disesuaikan agar pas dengan y = mx.

• stats    Opsional. Nilai logika yang menentukan apakah akan mengembalikan regresi statistik tambahan.

  • Jika stats TRUE, LINEST mengembalikan statistik regresi tambahan; sebagai hasilnya, array yang dikembalikan adalah {mn,mn-1,...,m1,b; sen,sen-1,...,se1,seb; r^2,sey; F,df; ssreg,ssresid}.

  • Jika stats FALSE atau dikosongkan, maka LINEST hanya mengembalikan koefisien m dan konstanta b.

    Regresi statistik tambahannya adalah sebagai berikut.

Ilustrasi berikut ini menunjukkan urutan tempat statistik regresi tambahan dikembalikan.

Keterangan

• Anda dapat menguraikan garis lurus dengan kemiringan dan garis potong y:

  Kelopak (m):
  Untuk menemukan kelereng garis, sering ditulis sebagai m, ambil dua titik pada garis, (x1,y1) dan (x2,y2); kelopak sama dengan (y2 - y1)/(x2 - x1).

  Potong y (b):
  Garis potong y, sering ditulis sebagai b, adalah nilai y pada titik di mana garis melewati sumbu y.

  Persamaan garis lurus adalah y = mx + b. Setelah mengetahui nilai m dan b, Anda dapat menghitung titik pada garis dengan memasukkan nilai y atau x ke dalam persamaan itu. Anda juga dapat menggunakan fungsi TREND.

• Ketika Anda hanya punya satu variabel data bebas x, Anda bisa mendapatkan nilai kemiringan dan garis potong y secara langsung dengan menggunakan rumus berikut ini:

  Lereng:
  =INDEX(LINEST(known_y,known_x's),1)

  Perpotongan Y:
  =INDEX(LINEST(known_y,known_x's),2)

• Keakuratan garis dihitung dengan fungsi LINEST tergantung dari derajat penyebaran dalam data Anda. Semakin linear data, semakin akurat model LINEST. LINEST menggunakan metode kuadrat terkecil untuk menentukan yang paling cocok untuk data. Ketika Anda hanya punya satu variabel bebas x, maka perhitungan untuk m dan b didasarkan pada rumus berikut ini:

  

  

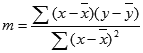
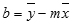
  di mana x dan y adalah sarana sampel; yaitu, x = AVERAGE(known x's) dan y = AVERAGE(known_y's).

• Fungsi line- and curve-fitting LINEST dan LOGEST dapat menghitung garis lurus atau kurva eksponensial terbaik yang sesuai dengan data Anda. Namun, Anda harus memutuskan mana dari dua hasil yang paling pas dengan data Anda. Anda dapat menghitung TREND(known_y,known_x) untuk garis lurus, atau GROWTH(known_y, known_x) untuk kurva eksponensial. Fungsi ini, tanpa argumen new_x , mengembalikan array nilai y yang diprediksi di sepanjang garis atau kurva tersebut pada titik data aktual Anda. Anda kemudian dapat membandingkan nilai yang diprediksi dengan nilai aktual. Anda mungkin ingin membuat bagan keduanya untuk perbandingan visual.

• Dalam analisis regresi, untuk setiap titik Excel menghitung selisih kuadrat antara nilai perkiraan y dengan nilai aktual y titik tersebut. Jumlah selisih kuadrat ini disebut jumlah residual kuadrat, ssresid. Kemudian Excel menghitung jumlah kuadrat total, sstotal. Ketika argumen const = TRUE atau dikosongkan, jumlah kuadrat total adalah jumlah selisih kuadrat antara nilai aktual y dengan nilai rata-rata y. Ketika argumen const = FALSE, jumlah total kuadrat adalah jumlah kuadrat nilai aktual y (tanpa mengurangi nilai rata-rata y dari masing-masing nilai individu y). Lalu regresi jumlah kuadrat, ssreg, dapat dicari dari: ssreg = sstotal - ssresid. Semakin kecil jumlah sisa kuadrat, dibandingkan dengan jumlah total kuadrat, semakin besar nilai koefisien determinasi, r², yang merupakan indikator seberapa baik persamaan yang dihasilkan dari analisis regresi menjelaskan hubungan di antara variabel. Nilai r² sama dengan ssreg/sstotal.

• Dalam beberapa kasus, satu atau lebih kolom X (dengan asumsi Y dan X berada di dalam kolom) mungkin tidak memiliki nilai ramalan dengan kehadiran kolom-kolom X lainnya. Dengan kata lain, menghilangkan satu atau lebih kolom X mungkin akan mengarah ke nilai ramalan Y yang sama akuratnya. Jika demikian, kolom-kolom X berlebihan ini tidak boleh ditulisi model regresi. Fenomena ini disebut “kolinearitas” karena kolom X yang berlebihan dapat diekspresikan sebagai jumlah kelipatan kolom-kolom X yang tidak berlebihan. Fungsi LINEST memeriksa apakah ada kolinearitas dan menghapus kolom-kolom X berlebihan dari model regresi saat fungsi itu mengenalinya. Kolom-kolom X yang dihapus dapat dikenali dalam keluaran LINEST sebagai memiliki koefisien 0 di samping nilai se 0. Jika satu atau lebih kolom dihapus sebagai berlebihan, df terpengaruh karena df tergantung dari jumlah kolom X yang benar-benar digunakan untuk tujuan peramalan. Untuk detail tentang komputasi df, lihat Contoh 4. Jika df berubah karena kolom-kolom X yang berlebihan dihapus, nilai sey dan F juga terpengaruh. Kolinearitas seharusnya relatif jarang pada praktiknya. Akan tetapi, ada satu kasus saat kejadian itu kemungkinan besar muncul, yaitu ketika beberapa kolom X hanya berisi nilai 0 dan 1 sebagai indikator apakah subyek yang ada dalam sebuah percobaan tergabung dengan kelompok tertentu atau bukan. Jika const = TRUE atau dikosongkan, maka fungsi LINEST secara efektif menyisipkan sebuah kolom X tambahan dari semua nilai 1 untuk meniru potongan tersebut. Jika Anda memiliki kolom berisi angka 1 untuk setiap subyek jika laki-laki, atau 0 jika bukan, dan Anda juga punya kolom berisi angka 1 untuk setiap subyek jika perempuan, atau 0 jika bukan, maka kolom terakhir ini berlebihan karena entri di dalamnya bisa didapat dari mengurangkan entri dalam kolom "indikator laki-laki" dari entri dalam kolom tambahan yang berisi semua nilai 1 yang ditambahkan oleh fungsi LINEST.

• Nilai df dihitung sebagai berikut, ketika tidak ada kolom X yang dihapus dari model karena kolinearitas: jika ada kolom kknown_x’s dan const = TRUE atau dikosongkan, maka df = n – k – 1. Jika const = FALSE, maka df = n - k. Dalam kedua kasus tersebut, setiap kolom X yang dihapus karena kolinearitas meningkatkan nilai df dengan menambah 1.

• Saat memasukkan konstanta array (seperti known_x's) sebagai sebuah argumen, gunakan koma untuk memisahkan nilai yang ada di dalam baris yang sama dan titik koma untuk memisahkan baris. Karakter pemisah mungkin berbeda tergantung dari pengaturan regional Anda.

• Perhatikan bahwa nilai y yang diramalkan oleh persamaan regresi mungkin tidak valid jika berada di luar rentang nilai y yang Anda gunakan untuk menentukan persamaannya.

• Alogaritme pokok yang digunakan dalam fungsi-fungsi LINEST berbeda dengan algoritme pokok yang digunakan dalam fungsi SLOPE dan INTERCEPT. Perbedaan antara algoritma ini dapat mengarah ke hasil yang berbeda ketika data tidak ditentukan dan kolinear. Misalnya, jika titik data argumen known_y's adalah 0 dan titik data argumen known_x's adalah 1:

  • LINEST mengembalikan nilai 0. Alogaritme fungsi LINEST dirancang untuk mengembalikan hasil yang masuk akal untuk data kolinear, dan dalam hal ini, setidaknya satu jawaban dapat ditemukan.

  • SLOPE dan INTERCEPT mengembalikan #DIV/0! . Algoritma fungsi SLOPE dan INTERCEPT dirancang untuk mencari hanya satu jawaban, dan dalam hal ini bisa ada lebih dari satu jawaban.

• Di samping menggunakan LOGEST untuk menghitung statistik untuk berbagai tipe regresi lainnya, Anda dapat menggunakan LINEST untuk menghitung rentang regresi jenis lain dengan memasukkan fungsi variabel x dan y sebagaimana rangkaian x dan y untuk LINEST. Misalnya, rumus berikut ini:

  =LINEST(yvalues, xvalues^COLUMN($A:$C))

  bekerja ketika Anda memiliki kolom tunggal berisi nilai y dan kolom tunggal untuk nilai x untuk menghitung kubik (polinomial orde 3) aproksimasi dari bentuk:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Anda dapat menyesuaikan rumus ini untuk menghitung regresi jenis lain, tapi dalam beberapa kasus rumus ini membutuhkan penyesuaian nilai keluaran dan statistik lainnya.

• Nilai uji F yang dikembalikan oleh fungsi LINEST berbeda dari nilai uji F yang dikembalikan oleh fungsi FTEST. LINEST mengembalikan statistik F, sedangkan FTEST mengembalikan probabilitas.

Contoh