Analüüsi tööriistapaketi kasutamine keeruliste andmeanalüüside jaoks

1. Klõpsake menüüs Fail nuppu Suvandid ja seejärel kategooriat Lisandmoodulid.

2. Valige ripploendist Halda väärtus Exceli lisandmoodulid ja klõpsake siis nuppu Mine.

   Kui kasutate rakendust Excel for Mac, valige failimenüüs Tööriistad > Exceli lisandmoodulid.

3. Märkige dialoogiboksis Lisandmoodulid ruut Analüüsi tööriistapakett ja klõpsake nuppu OK.

   • Kui loendis Saadaolevad lisandmoodulid pole väärtust Analüüsi tööriistapakett, klõpsake selle otsimiseks nuppu Sirvi.

   • Kui kuvatakse teade, et analüüsi tööriistapaketi lisandmoodul Analysis ToolPak pole teie arvutisse praegu installitud, klõpsake selle installimiseks nuppu Jah.

Dispersioonanalüüsi tööriistad hõlmavad dispersioonianalüüsi jaoks mitmesuguseid võimalusi. See, millist tööriista peaksite kasutama, sõltub tegurite ja testitavate populatsioonide puhul saadaolevate valimite arvust.

Üheteguriline dispersioonanalüüs

See tööriist analüüsib kahe või enama valimi andmete dispersiooni lihtsalt. Analüüs annab hüpoteesi, et iga valim tehakse sama alusjaotuse põhjal alternatiivse hüpoteesiga, et tõenäosusjaotused ei ole kõigi valimite puhul samad. Kui on ainult kaks näidet, saate kasutada töölehe funktsiooni T.TEST. Rohkem kui kahe näidisega ei ole T mugavat üldistust.Selle asemel saab kasutada funktsiooni TEST ja single Factor Anova mudelit.

Kaheteguriline kordusega dispersioonanalüüs

Sellest analüüsiriistast on kasu juhul, kui andmeid saab liigitada kahe erineva dimensioonina. Oletagem näiteks, et taimede kõrguse mõõtmiseks korraldatud katse raames on taimedele antud erinevat sorti väetist (nt A, B, C) ja lisaks on taimi hoitud erineval temperatuuril (nt madalal ja kõrgel). Võimalikke paare {väetis, temperatuur} on seega kokku kuus ning iga paari puhul on olemas võrdne arv taimede kõrguse vaatlusandmeid. Selle dispersioonanalüüsi tööriista abil saame testida järgmist:

• Kas taimede kõrgused erinevate väetisemarkide puhul pärinevad samast aluseks olevast populatsioonist. Selle analüüsi puhul ignoreeritakse temperatuure.

• Kas taimede kõrgused erinevate temperatuuritasemete puhul pärinevad samast aluseks olevast populatsioonist. Selle analüüsi puhul ignoreeritakse väetisemarke.

kas siis, kui arvesse on võetud esimeses loendipunktis väetisesortide puhul põhjustatud erinevuste mõju ning teises loendipunktis temperatuurist põhjustatud erinevuste mõju, on kõiki väärtuste {väetis, temperatuur} paare esindavad valimid võetud samast populatsioonist. Alternatiivne hüpotees väidab, et kindlate väärtuste {väetis, temperatuur} paaride teatud mõjud ei sõltu ainult väetisest või ainult temperatuurist põhjustatud erinevustest.

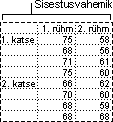
Kaheteguriline korduseta dispersioonanalüüs

Sellest analüüsiriistast on abi juhul, kui andmed on liigitatud kahe erineva dimensioonina (nagu ka kahe teguri ja kordamisega juhtumis). Selle tööriista kasutamisel aga eeldatakse, et iga paari (nt eelnevas näites iga paari {väetis, temperatuur}) puhul on tehtud ainult üks vaatlus.

Töölehe funktsioonid CORREL ja PEARSON arvutavad mõlema mõõdetava muutuja korrelatsioonikordaja, kui iga muutuja mõõdeti iga N-objekti puhul. (Iga puuduv vaatlus objekti kohta põhjustab analüüsis tähelepanuta jäävate põhjuste ignoreerimist.) Korrelatsioonianalüüsi tööriist on eriti kasulik juhul, kui iga N-objekti kohta on rohkem kui kaks mõõdetav muutujat. See annab väljundtabeli ehk korrelatsioonimaatriksi, mis näitab igale võimalikule mõõdetavate muutujate paarile rakendatud KORREL ( või PEARSON) väärtust.

Korrelatsioonikordaja, nagu ka kovariatsioon, on mõõtühik, mille ulatuses kaks mõõdetava muutujat "varieeruvad koos". Erinevalt kovariatsioonist mastaabitakse korrelatsioonikordaja nii, et selle väärtus oleks sõltumatu ühikutest, milles väljendatakse kahte mõõtühikut. (Näiteks kui kaks mõõtemuutujat on kaal ja kõrgus, siis korrelatsioonikordaja väärtust ei muudeta, kui kaal teisendatakse naeltest kilogrammideks.) Korrelatsioonikordaja väärtus peab olema vahemikus -1 kuni +1 (k.a).

Korrelatsioonianalüüsi tööriista abil saate iga mõõdetavate muutujate paari analüüsida, määratlemaks, kas mõlemad mõõdetavad muutujad kalduvad koos liikuma – kas ühe muutuja suured väärtused kalduvad seostuma teise muutuja suurte väärtustega (positiivne korrelatsioon), kas ühe muutuja väikesed väärtused kalduvad seostuma teise muutuja suurte väärtustega (negatiivne korrelatsioon) või kas mõlema muutuja väärtused kalduvad olema omavahel seostamatud (nullilähedane korrelatsioon).

Tööriistu Korrelatsioon ja Kovariatsioon saab koos kasutada olukorras, kus teatud isikutekogumi puhul vaadeldakse N-hulka erinevaid mõõdetavaid muutujaid. Mõlemad tööriistad (Korrelatsioon ja Kovariatsioon) koostavad väljundtabeli ehk maatriksi, kus kuvatakse vastavalt siis iga mõõdetavate muutujate paari korrelatsioonikordaja või kovariatsioon. Erinevus on selles, et korrelatsioonikordajad paigutatakse skaalal vahemikku -1 kuni +1 (kaasa arvatud). Vastavaid kovariatsioone skaalale ei paigutata. Nii korrelatsioonikordaja kui ka kovariatsioon mõõdavad kahe muutuja koos muutumise ulatust.

Kovariatsiooniriist arvutab töölehefunktsiooni COVARIANCE väärtuse. P iga mõõdetavate muutujate paari kohta. (COVARIANCE'i otsene kasutamine. P, mitte kovariatsioon, on mõistlik alternatiiv, kui on ainult kaks mõõdetavat muutujat, st N=2.) Kovariatsiooniriista väljundtabeli diagonaali kirje reas i, veerus i on i-nda mõõdetava muutuja kovariatsioon iseendaga. See on ainult selle muutuja populatsiooni dispersioon, mille arvutab töölehe funktsioon VAR.P.

Kovariatsioonianalüüsi tööriista abil saate iga mõõdetavate muutujate paari analüüsida, määratlemaks, kas mõlemad mõõdetavad muutujad kalduvad koos liikuma – kas ühe muutuja suured väärtused kalduvad seostuma teise muutuja suurte väärtustega (positiivne kovariatsioon), kas ühe muutuja väikesed väärtused kalduvad seostuma teise muutuja suurte väärtustega (negatiivne kovariatsioon) või kas mõlema muutuja väärtused kalduvad olema omavahel seostamatud (nullilähedane kovariatsioon).

Kirjeldava statistika analüüsiriist loob sisendvahemikus leiduvate andmete kohta ühe muutujaga statistika aruande, sisaldades teavet andmete keskmise ja hajuvuse kohta.

Eksponentsilumise analüüsiriist ennustab eelneva perioodi prognoosil põhinevat ja selle vea osas täpsustatud väärtust. Tööriist kasutab silumiskonstanti a, mille suurusjärk määratleb, kui täpselt reageerivad prognoosid eelmise prognoosi vigadele.

F-Testi analüüsitööriist Kaks valimit dispersioonide jaoks teostab kahe populatsioonidispersiooni võrdlemiseks kahe valimiga F-testi.

Näiteks võite F-Testi tööriista kasutada kahe meeskonna ujumisvõistluses saavutatud aegade valimite osas. Tulemi saamiseks võrdleb tööriist nullhüpoteesi, et mõlemad valimid pärinevad võrdse dispersiooniga jaotustest, alternatiivse hüpoteesiga, et vastavate jaotuste dispersioonid pole võrdsed.

Tööriist arvutab F-statistiku (ehk F-suhte) f-väärtuse. Kui f-väärtus on 1 lähedal, siis osutab see, et aluseks olevad populatsioonidispersioonid on võrdsed. Kui väljundtabelis on f < 1 "P(F <= f) ühepoolne", annab see tõenäosuse, et võrdsete populatsioonidispersioonide puhul on F-statistiku väärtus vaatlemisel väiksem kui f, ning "F-statistiku kriitiline ühepoolne" annab valitud olulisuse nivoo alfa puhul tulemiks, et kriitiline väärtus on väiksem kui 1. Kui f > 1, "P(F <= f) ühepoolne", annab see tõenäosuse, et võrdsete populatsioonidispersioonide puhul on F-statistiku väärtus vaatlemisel suurem kui f, ning "F-statistiku kriitiline ühepoolne" annab alfa kriitiliseks väärtuseks rohkem kui 1.

Fourier' analüüsi tööriist lahendab lineaarsüsteemides ülesandeid ja analüüsib perioodilisi andmeid, kasutades andmete teisendamiseks kiire Fourier' teisenduse (FFT) meetodit. See tööriist toetab ka pöördteisendusi, mille puhul teisendatud andmete pööre tagastab algandmed.

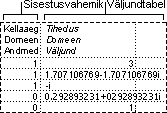
Histogrammi analüüsiriist arvutab andmete lahtrivahemiku ja lahtrisalvede individuaalsed ja kumulatiivsed sagedused. See tööriist loob väärtuse andmehulgas esinemise kordade arvu andmed.

Näiteks 20 õpilasega klassis saate määratleda punktisummade jaotuse hindekategooriates. Histogrammitabelis on ära toodud nii hinnete piirid kui ka alumise piirangu ja praeguse piirangu vahele jäävate punktisummade arv. Kõige sagedamini esinev punktisumma on andmete mood.

Jooksva keskmise analüüsiriist ennustab prognoosiperioodi väärtusi, võttes aluseks muutuja keskmise väärtuse kindla arvu eelnevate perioodide jooksul. Jooksev keskmine pakub trenditeavet, mille kõigi ajalooliste andmete lihtne keskmine peidaks. Selle tööriista abil saate prognoosida müüki, laoseisu või muid trende. Iga prognoosiväärtus põhineb järgmisel valemil.

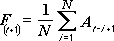
Kus:

• N on jooksvasse keskmisse kaasatavate eelmiste perioodide arv

• A j on tegelik väärtus j-hetkel

• F j on prognoositud väärtus j-hetkel

Juhuarvude loomise analüüsiriist täidab vahemiku sõltumatute juhuarvudega, mis pärinevad ühest jaotusest (kui jaotusi on mitu). Populatsiooni objekte saate iseloomustada tõenäosusjaotusega. Näiteks saate normaaljaotusega iseloomustada isikute pikkuste populatsiooni või kasutada kulli ja kirja viskamise tulemite populatsiooni iseloomustamiseks kahe võimaliku tulemuse Bernoulli jaotust.

Analüüsiriist Rank (Reit) ja Percentile (Protsentiili analüüs) koostab tabeli, mis sisaldab iga väärtuse järgarvu ja protsentuaalset järku andmekogumis. Saate analüüsida andmekogumi väärtuste suhtelist positsiooni. See tööriist kasutab töölehefunktsioone RANK. EQ jaPERCENTRANK. INC. Kui soovite arvesse võtta seotud väärtusi, kasutage funktsiooni RANK. Funktsioon EQ , mis kohtleb seotud väärtusi sama asukohaga väärtustega või kasutab funktsiooni RANK.Funktsioon AVG , mis tagastab seotud väärtuste keskmise asukoha.

Regressiooni analüüsiriist teostab lineaarregressiooni analüüsi vähimruutude meetodi abil, et sobitada sirget erinevate vaatlustega. Saate analüüsida, kuidas mõjutavad ühe või mitme sõltumatu muutuja väärtused ühte sõltuvat muutujat. Näiteks saate analüüsida, millist mõju avaldavad sportlase tulemustele sellised tegurid nagu vanus, pikkus ja kaal. Tulemuste andmete kogumi põhjal saate igale tegurile määrata teatud osakaalu tulemuste mõõtmisel ja tulemeid seejärel kasutada uue, testimata sportlase tulemuste ennustamiseks.

Regressiooniriist kasutab töölehefunktsiooni LINEST.

Valiku analüüsiriist loob populatsioonivalimi, käsitledes populatsioonina sisendvahemikku. Kui populatsioon on töötlemiseks või kaardistamiseks liiga suur, võite kasutada esindavat valimit. Samuti võite luua valimi, mis sisaldab ainult tsükli teatud osast pärinevaid väärtusi, kui arvate, et sisendandmed on perioodilised. Kui sisendvahemik sisaldab näiteks kvartaalseid müüginäitajaid, võite valimi koostamisel kasutada perioodimäära neli, et paigutada väljundvahemikku sama kvartali väärtused.

Kahe valimiga t-Testi analüüsiriistad testivad iga valimi aluseks olevate populatsioonide aritmeetiliste keskmiste võrdsust. Kolme tööriista puhul lähtutakse erinevatest eeldustest: populatsioonide dispersioonid on võrdsed, populatsioonide dispersioonid pole võrdsed, ning kaks valimit esindavad samade objektide töötlemiseelseid ja töötlemisjärgseid vaatlusi.

Kõigi kolme tööriista puhul arvutatakse t-statistiku väärtus t, mis kuvatakse väljundtabelis nimega "t Stat". Sõltuvalt andmetest võib see väärtus t olla nii negatiivne kui ka mittenegatiivne. Eeldades, et analüüsi aluseks olevate populatsioonide aritmeetilised keskmised on võrdsed, siis kui t < 0, "P(T <= t) ühepoolne", annab see tõenäosuse, et t-statistiku vaadeldav väärtus oleks negatiivsem kui t. Kui t >=0, "P(T <= t) ühepoolne", annab see tõenäosuse, et t-statistiku vaadeldav väärtus oleks positiivsem kui t. "t-statistiku kriitiline ühepoolne" annab katkestusväärtuse, mille puhul väärtusest "t-statistiku kriitiline ühepoolne" suurema või sellega võrdse väärtuse vaatlemise tõenäosus on alfa.

"P(T <= t) kahepoolne" annab tõenäosuse, et t-statistiku vaadeldav väärtus oleks absoluutväärtuselt suurem kui t. "P-statistiku kriitiline kahepoolne" annab katkestusväärtuse, mille puhul väärtusest "P-statistiku kriitiline kahepoolne" absoluutväärtuselt suurema t-statistiku väärtuse vaatlemise tõenäosus on alfa.

t-test: kahe valimi keskväärtuste arvutamiseks paaris

Paaristesti saate kasutada kui valimis on vaatlused loomupäraselt paaris (nt valimigruppi on testitud kaks korda – enne ja pärast eksperimenti). See analüüsiriist ja selle valem sooritavad kahe paarisvalimi Studenti t-testi, et kontrollida, kas vaatlused, mis on võetud enne ja pärast töötlemist, on tõenäoliselt pärit võrdsete populatsiooni keskväärtustega jaotustest. t-test ei eelda mõlema populatsiooni dispersiooni võrdsust.

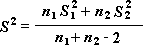
t-test: kaks valimit võrdsete dispersioonide eeldusega

See analüüsiriist sooritab kahe valimi Studenti t-testi. t-test eeldab, et kaks andmehulka pärinevad sama dispersiooniga jaotustest. Seda nimetatakse püsihajuvaks t-testiks. Selle t-testiga saate määrata, kas kaks valimit pärinevad tõenäoliselt jaotustest, mille populatsioonidel on võrdne keskväärtus.

t-test: kaks valimit ebavõrdsete dispersioonide eeldusega

See analüüsiriist sooritab kahe valimi Studenti t-testi. See t-test eeldab, et kaks andmehulka pärinevad ebavõrdse dispersiooniga jaotustest. Seda nimetatakse muuthajuvaks t-testiks. Nagu eelmise, võrdse dispersiooni puhul, saate seda testi kasutada selleks, et määratleda, kas kaks valimit pärinevad tõenäoliselt jaotustest, millel on võrdsed populatsiooni keskväärtused. Kasutage seda testi juhul, kui kahes valimis on eristuvaid üksusi. Kasutage järgmises näiteskirjeldatud paaristesti üksuste ühe kogumi olemasolu puhul ja kui kaks valimit esindavad iga üksuse mõõtmisi enne ja pärast töötlemist.

Statistilise väärtuse t määratlemiseks kasutatakse järgmist valemit.

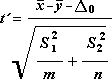
Järgmist valemit kasutatakse vabadusastmete arvutamiseks: df. Kuna arvutuse tulem pole tavaliselt täisarv, ümardatakse väärtus df lähima täisarvuni, et saada kriitiline väärtus tabelist t. Exceli töölehefunktsioon T.Funktsioon TEST kasutab arvutatud df-väärtust ümardamata, kuna T jaoks on võimalik arvutada väärtus.Test mitteintegraalarvuga df. Nende erinevate vabadusastmete määramisel lähtutakse T tulemustest.TEST ja see t-Testi tööriist erinevad ebavõrdsete dispersioonide puhul.

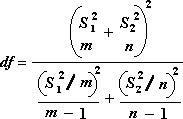
Z-test: analüüsiriist Two Sample for Means sooritab teadaolevate dispersioonidega vahendite puhul kahe valimi z-testi. Seda tööriista kasutatakse nullhüpoteesi kontrollimiseks, et kahe populatsioonivahendi vahel ei ole erinevust kas ühepoolsete või kahepoolsete alternatiivsete hüpoteeside suhtes. Kui dispersioonid pole teada, siis töölehefunktsioon Z.Selle asemel tuleks kasutada funktsiooni TEST.

z-Testi tööriista kasutamisel olge väljundi tõlgendamisel ettevaatlik. "P(Z <= z) ühepoolne" on tegelikult P(Z >= ABS(z)) – tõenäosus, et z-väärtus on 0-st kaugemal samas suunas nagu vaadeldud z-väärtus, kui populatsioonide keskmiste vahel pole erinevusi. "P(Z <= z) kahepoolne" on tegelikult P(Z >= ABS(z) või Z <= -ABS(z)) – tõenäosus, et z-väärtus on 0-st kummaski suunal kaugemal kui vaadeldud z-väärtus, kui populatsioonide keskmiste vahel pole erinevusi. Kahepoolne tulem on lihtsalt kahega korrutatud ühepoolne tulem. z-Testi tööriista saab kasutada ka juhul, kui nullhüpotees on see, et kahe populatsiooni keskmistel on teatud kindel nullist erineva väärtusega erinevus. Näiteks saate selle testi abil määratleda kahe automudeli jõudluse erinevusi.