本文將說明 Microsoft Excel 中 LINEST 函數的公式語法及使用方式。
描述
LINEST 函數使用「最小平方」法計算資料最適合的直線,以計算出該線的統計資料,然後傳回描述該線的陣列。 您也可以結合 LINEST 與其他函數來計算其他不明參數的線性模型統計資料,包括多項式、對數、指數和冪級數。 因為此函數傳回的是數值陣列,所以它必須以陣列公式的方式輸入。 本文中範例下面都有指示說明。
此直線的方程式為:
y = mx + b
-或-
y = m1x1 + m2x2 + ... + b
如果有多個範圍的 x 值,其中因變數 y 值是自變數 x 值的函數。 m 值為對應每一個 x 值的係數,而 b 則為常數值。 請注意 y、x 與 m 可以為向量。 LINEST 函數傳回的陣列為 {mn,mn-1,...,m1,b}。 LINEST 也可以傳回額外的迴歸統計值。
語法
LINEST(known_y's, [known_x's], [const], [stats])
LINEST 函數語法具有下列引數:
語法
-
known_y's 必要。 這是在 y = mx + b 關係中一組已知的 y 值。
-
如果 known_y's 的範圍在單一欄中,則 known_x's 的每一欄將被視為一個獨立的變數。
-
如果 known_y's 的範圍是包含在單一列中,則 known_x's 的每一列將被視為一個獨立的變數。
-
-
known_x's 選擇性。 這是在 y = mx +b 關係中一組已知的 x 值。
-
known_x's 的範圍可包含一或多組變數。 如果只用到一個變數,known_y's 與 known_x's 可以是任何圖形的範圍,只要兩者有相同的維數即可。 如果使用多個變數,則 known_y's 必須是個向量 (也就是,高度為一列或寬度為一欄的範圍)。
-
如果省略 known_x's,則假定它是與 known_y's 大小相同的陣列 {1,2,3,...}。
-
-
const 選擇性。 這是指定是否強迫常數 b 等於 0 的邏輯值。
-
如果 const 為 TRUE 或被省略了,b 會以正常方式計算。
-
如果 const 為 FALSE,b 將被設定為 0,並調整 m 值使其符合 y = mx。
-
-
stats 選擇性。 這是一個指定是否要傳回額外迴歸統計值的邏輯值。
-
如果 stats 為 TRUE,LINEST 會 傳回額外的回歸統計值;因此,傳回的陣列為 {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}。
-
如果 stats 為 FALSE 或省略,LINEST 就只會傳回 m 係數和常數 b。
額外的迴歸統計值如下:
-
|
統計值 |
描述 |
|---|---|
|
se1,se2,...,sen |
係數 m1,m2,...,mn 的標準誤差值。 |
|
seb |
常數 b 的標準誤差值 (當 const 為 FALSE 時,seb = #N/A)。 |
|
r2 |
決定係數。 比較 y 的估計值與實際值,其值為 0 到 1。 如果是 1,表示樣本完全相關,即 y 的估計值與實際值沒有差異。 另一方面如果決定係數是 0,迴歸方程式對預測 y 值是沒有幫助的。 如需如何計算2 的相關信息,請參閱本主題稍後的。 |
|
sey |
y 估計值的標準誤差。 |
|
F |
F 統計值或 F 觀察值。 使用 F 統計值來決定自變數和因變數間的關係是否是巧合的。 |
|
df |
自由度。 使用自由度協助您於統計的表格中找出 F 臨界值。 將您在表格中找到的值與 LINEST 傳回的 F 統計值相互比較,以決定此模式的信賴區間。 有關如何計算 df 的詳細資訊,請參閱本主題下的<註解>。 範例 4 會示範 F 及 df 的用法。 |
|
ssreg |
迴歸平方和。 |
|
ssresid |
剩餘平方和。 有關如何計算 ssreg 及 ssresid 的詳細資訊,請參閱本主題下的<註解>。 |
下圖顯示額外的迴歸統計值傳回的次序。

註解
-
您可用斜率和 Y 截距來描述任何一個直線:
斜率 (m) : 若要尋找通常寫為 m 的線條斜率,請在行上取得兩點, (x1,y1) , (x2,y2) ;斜率等於 (y2 - y1) / (x2 - x1) 。
Y 截距 (b) : 線條的 y 截距通常寫成 b,是線條交叉 y 軸時 y 的值。
直線方程式為 y = mx + b。 在得知 m 和 b 值之後,您可以藉由把 y 或 x 值插入方程式中,以計算在線上的任何一點。 您也可以使用 TREND 函數。
-
當您只有一個自變數 x 時,您可以直接使用下面的公式來求得斜率和 Y 截距值:
坡: =INDEX (LINEST (known_y's,known_x 的) ,1)
Y 截距: =INDEX (LINEST (known_y's,known_x 的) ,2)
-
LINEST 函數計算線的精確度取決於資料的散佈程度。 資料散佈的越具線性,LINEST 模型就越精確。 LINEST 使用最小平方法求出資料的最適合直線。 當僅有一個自變數 x 時,m 和 b 是根據以下公式計算而來:
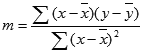
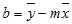
其中,x 及 y 為樣本平均數,也就是 x = AVERAGE(known x's) 及 y = AVERAGE(known_y's)。
-
線調整函數 LINEST 及曲線調整函數 LOGEST 可以計算出您資料的最適合直線或指數曲線。 不過,您必須決定哪個結果最適用於您的資料。 您可以用 TREND(known_y's,known_x's) 來計算直線,或 GROWTH(known_y's、known_x's) 來計算指數曲線。 在沒有 new_x's 引數時,這些函數會傳回沿著該線或曲線在實際的資料點所預測的 y 值陣列。 然後您就可以比較預測值和實際值。 您亦可以繪成圖表以視覺比較其差異。
-
在迴歸分析中,Excel 會針對每個點的估計 y 值及實際 y 值之間,計算該點的平方差。 這些的平方差的總和稱為剩餘平方和,ssresid。 Excel 接著會計算總平方和,sstotal。 當 const 引數 = TRUE 或省略時,總平方和為實際 y 值和平均 y 值之間平方差的總和。 當 const 引數 = False 時,總平方和則為實際 y 值 (不減去個別 y 值的平均 y 值) 的平方和。 然後可依據 ssreg = sstotal - ssresid 求得迴歸平方和,ssreg。 相對於總平方和,剩餘平方和越小,決定係數 r2 的值越大,這是一個指示器,說明回歸分析所產生的方程式如何解釋變數之間的關係。 r2 的值等於 ssreg/sstotal。
-
在大多數的例子中,一個或多個 X 欄 (假設 Y’s 及 X’s 位於欄中) 在其他 X 欄中或許沒有額外的預測值。 換句話說,排除一個或多個 X 欄可能會得到相同精確的預測 Y 值。 在該例中,多餘的 X 欄在迴歸模型中應省略。 此現象稱為「共線性」,因為任何多餘的 X 欄都可被表示為多重非多餘 X 欄的總和。 LINEST 會檢查共線性,並且在從迴歸模型中辨識出任何多餘的 X 欄時將之移除。 在 LINEST 輸出中被移除的 X 欄會以係數 0 及 0 se 值表示。 如果有一個或多個欄被當做是多餘的而遭移除,則 df 將會被影響,因為 df 是根據實際用於預測性目的之 X 欄的數量而定。 關於 df 計算的詳細資料,請參閱範例 4。 如果 df 因移除多餘的 X 欄而受到變更,也會連帶影響 sey 值及 F。 共線性在實際上應是很少見的。 然而,當某些 X 欄包括只有 0 及 1 的值做為指標 (不論在實驗中實驗對象是否為特定群組的成員) 時,就可能發生。 如果 const = TRUE 或省略,LINEST 函數會於所有 1 值實際插入額外的 X 欄以做為截距的模型。 如果您的每個實驗對象為男性時是 1,不是時為 0,以及您的每個實驗對象為女性時是 1,不是時為 0,則後欄是多餘的,因為只要從 LINEST 函數新增的所有 1 值的額外欄項目中減去「男性指標」欄位中的項目,即可取得該欄位中的項目。
-
基於共線性,在沒有任何 X 欄從模型中移除時,df 之值的計算方式如下:如果 known_x’s 有 k 個欄位,且 const = TRUE 或省略,則 df = n – k – 1。 如果 const = FALSE,則 df = n - k。 在這兩個例子中,因為共線性而移除的每個 X 欄會造成 df 的值增加 1。
-
當引數 (如 known_x's) 以常數陣列方式輸入時,請使用逗號 (,) 來分隔包含在同列中的各值,並使用分號 (;) 來分隔各列。 分隔字元可能依地區選項而有所不同。
-
請注意,如果由迴歸方程式所求得的 y 估計值超出您用以計算方程式的 y 值範圍,則該值可能不正確。
-
LINEST 函數中所使用的基本演算法,不同於 SLOPE 及 INTERCEPT 函數中使用的基本演算法。 當資料未確定且未共線時,這些演算法之間的差異會導致不同的結果。 例如,如果 known_y's 引數的資料點為 0,而 known_x's 引數的資料點為 1:
-
LINEST 會傳回 0 的值。 LINEST 函數演算法是設計來傳回合理的共線資料結果,而在此情況中,至少可以找到一個答案。
-
SLOPE 與 INTERCEPT 會傳回 #DIV/0! 的錯誤。 SLOPE 和 INTERCEPT 函數的演算法是設計來尋找單一個答案,而在此情況下,可能有多個答案。
-
-
除了使用 LOGEST 計算其他迴歸類型的統計值之外,您可使用 LINEST 計算其他迴歸類型的範圍,只要輸入 x 和 y 變數的函數做為 LINEST 的 x 和 y 數列即可。 例如,下列公式:
=LINEST(yvalues,xvalues^COLUMN($A:$C))
當您只有單獨一欄 y 值和單獨一欄 x 值用來計算下列公式的立方 (順序 3 的多項式) 近似值時就可以使用:
y = m1*x + m2*x^2 + m3*x^3 + b
您可以調整此公式以計算其他迴歸類型,不過在某些情況下,需要調整輸出值和其他統計值。
-
LINEST 函數傳回的 F 檢定值,與 FTEST 函數傳回的 F 檢定值不同。 LINEST 會傳回 F 統計值,而 FTEST 則傳回機率。
範例
範例 1:斜率和 Y 截距
請在下列表格中複製範例資料,再將之貼到新 Excel 工作表中的儲存格 A1。 若要讓公式顯示結果,請選取公式,按 F2,然後再按 Enter。 如有需要,您可以調整欄寬來查看所有資料。
|
已知的 y |
已知的 x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
結果 (斜率) |
結果 (y 截距) |
|
2 |
1 |
|
公式 (儲存格 A7:B7 中的陣列公式) |
|
|
=LINEST(A2:A5,B2:B5,,FALSE) |
範例 2:簡單的線性迴歸
請在下列表格中複製範例資料,再將之貼到新 Excel 工作表中的儲存格 A1。 若要讓公式顯示結果,請選取公式,按 F2,然後再按 Enter。 如有需要,您可以調整欄寬來查看所有資料。
|
月 |
銷售額 |
|---|---|
|
1 |
$3,100 |
|
2 |
$4,500 |
|
3 |
$4,400 |
|
4 |
$5,400 |
|
5 |
$7,500 |
|
6 |
$8,100 |
|
公式 |
結果 |
|
=SUM(LINEST(B1:B6, A1:A6)*{9,1}) |
$11,000 |
|
根據第 1 個月到第 6 個月的銷售額計算第 9 個月的銷售額估計值。 |
範例 3:多元線性迴歸
請在下列表格中複製範例資料,再將之貼到新 Excel 工作表中的儲存格 A1。 若要讓公式顯示結果,請選取公式,按 F2,然後再按 Enter。 如有需要,您可以調整欄寬來查看所有資料。
|
樓層面積 (x1) |
辦公室間數 (x2) |
出入口數 (x3) |
屋齡 (x4) |
估定值 (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
$142,000 |
|
2333 |
2 |
2 |
12 |
$144,000 |
|
2356 |
3 |
1.5 |
33 |
$151,000 |
|
2379 |
3 |
2 |
43 |
$150,000 |
|
2402 |
2 |
3 |
53 |
$139,000 |
|
2425 |
4 |
2 |
23 |
$169,000 |
|
2448 |
2 |
1.5 |
99 |
$126,000 |
|
2471 |
2 |
2 |
34 |
$142,900 |
|
2494 |
3 |
3 |
23 |
$163,000 |
|
2517 |
4 |
4 |
55 |
$169,000 |
|
2540 |
2 |
3 |
22 |
$149,000 |
|
-234.2371645 |
||||
|
13.26801148 |
||||
|
0.996747993 |
||||
|
459.7536742 |
||||
|
1732393319 |
||||
|
公式 (在 A19 中輸入的動態數位公式) |
||||
|
=LINEST(E2:E12,A2:D12,TRUE,TRUE) |
範例 4 - 使用 F 和 r2 統計數據
在上述範例中,決定係數 r2 為 0.99675 (在 LINEST) 輸出中看到單元格 A17,這表示自變數與銷售價格之間有很強的關係。 您可以使用 F 統計值來判定這樣高的 r2 是否純屬巧合。
假定事實上所觀測的變數之間沒有關係,但您已抽出了 11 個非常特殊的辦公大樓樣本資料,以致於統計分析誤判有強烈關係。 這種總結出錯誤關係的機率稱為 Alpha。
LINEST 函數輸出中的 F 及 df 值可用來評估較高 F 值的偶發機率。 F 可以與已發佈的 F 分配表格中的臨界值相比較,或是使用 Excel 中的 FDIST 函數來計算較大 F 值的偶發機率。 適當的 F 分配具有 v1 和 v2 的自由度。 如果 n 是資料點的個數且 const = TRUE 或省略,則 v1 = n – df – 1 且 v2 = df。 (如果 const = False,則 v1 = n – df 且 v2 = df)。 FDIST函數 — 語法為 FDIST(F,V1,v2) — 會傳回較高的 F 值偶發機率。 在此範例中,df = 6 (儲存格 B18) 及 F = 459.753674 (儲存格 A18)。
假定 Alpha 值為 0.05、v1 = 11 – 6 – 1 = 4 且 v2 = 6,F 的臨界等級為 4.53。 由於 F = 459.753674 比 4.53 高出許多,而這麼高的 F 值極不可能是偶發的。 (因為 Alpha = 0.05,known_y's 與 known_x's 之間無關聯的假設會在 F 超出臨界等級 4.53 時會遭到拒絕)。 您可以使用 Excel 中的 FDIST 函數來取得這麼高的 F 值偶發的機率。 例如,FDIST(459.753674, 4, 6) = 1.37E-7 的機率極小。 您可以推斷,無論是在表格中尋找 F 臨界等級,或使用 FDIST 函數,迴歸方程式都能夠有效地預測這個區域內的辦公大樓的估價。 請記住,一定要使用在前一段落中得出的 v1 和 v2 正確值。
範例 5:計算 T 統計值
另一個假設檢定可判斷每一個斜率係數在評估範例 3 中辦公大樓的估價時是否有用。 例如,檢定屋齡係數對於統計的意義,將 -234.24 (屋齡斜率係數) 除以 13.268 (在儲存格 A15 中屋齡係數的估計標準誤差)。 以下是 T 觀察值的公式:
t = m4 ÷ se4 = -234.24 ÷ 13.268 = -17.7
如果 t 的絕對值夠高,則可以推斷出斜率係數在評估範例 3 中,辦公大樓的估價時是有用的。 下表顯示 4 個 T 觀察值的絕對值。
查閱統計學手冊中的表格時,您可找到自由度是 6 且 Alpha = 0.05 時,雙尾檢定的 T 臨界值為 2.447。 這個臨界值也可使用 Excel 的 TINV 函數來找到。 TINV(0.05,6) = 2.447。 因為 T (17.7) 的絕對值大於 2.447,所以屋齡是估算辦公大樓價值時的重要變數。 其他每一個自變數亦可以用相同的方式檢定其個別的統計意義。 以下項目是每個自變數的 T 觀察值:
|
變數 |
T 觀察值 |
|---|---|
|
樓層面積 |
5.1 |
|
辦公室間數 |
31.3 |
|
出入口個數 |
4.8 |
|
屋齡 |
17.7 |
這些數值都大於 2.447 的絕對值;因此,所有使用於迴歸方程式中的自變數在預測這個區域辦公大樓的估計價值都是很有用的。










