如果您需要开展复杂的统计或工程分析,则可使用分析工具库以节省步骤和时间。 为每项分析提供数据和参数,此工具将使用适当的统计或工程宏函数来计算并将结果显示在输出表格中。 除了输出表格,某些工具还生成图表。
这些数据分析函数一次只能在一个工作表上使用。 当您在分组的工作表上执行数据分析时,结果将显示在第一个工作表,而其余的工作表中则显示清空格式的表格。 要对其余的工作表执行数据分析,请使用分析工具分别对每个工作表重新计算。
分析工具库包括下文所述的工具。 要使用这些工具,请在“数据”选项卡上的“分析”组中单击“数据分析”。 如果“数据分析”命令不可用,则需要加载分析工具库加载宏程序。
-
单击“文件”选项卡,单击“选项”,然后单击“加载宏”类别。
-
在“管理”框中,选择“Excel 加载宏”,再单击“转到”。
如果使用 Excel for Mac,则在文件菜单中转到“工具”>“Excel 加载项”。
-
在“加载项”框中,选中“分析工具库”复选框,然后单击“确定”。
-
如果“可用加载宏”框中未列出“分析工具库”,请单击“浏览”以找到它。
-
如果系统提示计算机当前未安装分析工具库,请单击“是”进行安装。
-
注意: 若要包括用于分析工具库的 Visual Basic for Application (VBA) 函数,可以按加载分析工具库的相同方式加载“分析工具库 - VBA”加载宏。 在“可用加载宏”框中,选中“分析工具库 - VBA”复选框。
方差分析工具提供了不同类型的方差分析。 您应根据要测试的样本总体中的因素数和样本数决定要使用的工具。
方差分析:单因素
此工具对两个或两个以上样本的数据方差执行简单的分析。 此分析可提供一种假设检验,该假设的内容是:每个样本都取自相同基础概率分布,这与对所有样本来说基础概率分布都不相同的假设相反。 如果只有两个样本,则您可以使用工作表函数 T.TEST。 对于两个以上的样本,并无 T.TEST 的适宜推广形式,此时可调用单因素方差分析模型。
方差分析:包含重复的双因素
此分析工具可用于分析按两个不同的维度归类的数据。 例如,在测量植物高度的实验中,可能会对植物施加不同品牌的化肥(例如,A、B、C),也可能在不同温度(例如,低、高)中培养植物。 对于 {化肥,温度} 的六种可能配对中的每一种,我们对植物高度取相同数量的观测值。 使用此方差分析工具,我们可以测试:
-
施加不同品牌化肥的植物高度是否取自相同的基础样本总体。 此分析将忽略温度。
-
不同温度级别中种植的植物高度是否取自相同的基础样本总体。 此分析将忽略化肥品牌。
是否考虑到在第 1 步中发现的不同品牌化肥之间的差异以及第 2 步中不同温度之间差异的影响,代表所有 {化肥,温度} 值配对的 6 个样本取自相同的样本总体。 另一种假设是仅基于化肥或温度来说,这些差异会对特定的 {化肥,温度} 值配对有影响。
方差分析:无重复的双因素
此分析工具可用于分析按两个不同的维度归类的数据(如包含重复的双因素案例)。 但是,对于此工具,假设每个配对只有一个观测值(例如,上面的示例中的每个 {化肥,温度} 配对)。
当对 N 个主体中的每一个变量进行观测时,CORREL 和 PEARSON 工作表函数都可计算两个测量变量之间的相关系数。 (缺少任何主体的观测值将导致该主体在分析中被忽略。 )当 N 个主体中的每一个均具备两个以上的测量变量时,相关系数分析工具则尤为有用。 它会提供一个输出表格,即相关矩阵,显示应用到每对可能的测量变量的 CORREL(或 PEARSON)函数值。
相关系数与协方差相似,是两个测量变量之间关联变化程度的指标。 与协方差不同的是,相关系数是比例值,因此它的值与用来表示两个测量变量的单位无关。 (例如,如果两个测量变量为重量和高度,则将重量从英镑转换为公斤时,相关系数的值不会改变。 )任何相关系数的值必须介于 -1 和 +1 之间(包括 -1 和 +1)。
可以使用相关系数分析工具来检验每对测量值变量,以便确定两个测量值变量是否趋向于同时变动,即,一个变量的较大值是否趋向于与另一个变量的较大值相关联(正相关);或者一个变量的较小值是否趋向于与另一个变量的较大值相关联(负相关);或者两个变量的值趋向于互不关联(相关系数近似于零)。
当您需要观测一组个体的 N 个不同测量变量时,相关系数和协方差工具都可用于相同的设置中。 相关系数和协方差工具会各自提供一个输出表格,即一个矩阵,分别显示每对测量变量之间的相关系数和协方差。 不同之处在于,相关系数可以调整,其值介于 -1 和 +1 之间(包括 -1 和 +1)。 相应的协方差则无法调整。 相关系数和协方差均为两个变量之间关联变化程度的指标。
协方差工具为每对测量变量计算工作表函数 COVARIANCE.P 的值。 (当仅有两个测量变量,即 N=2 时,合理的选择是直接使用 COVARIANCE.P,而无需使用协方差工具。 )协方差工具输出表格对角线上位于第 i 行和第 i 列的条目即为第 i 个测量变量与其自身的协方差。 这即为由工作表函数 VAR.P 计算的该变量的总体方差。
可以使用“协方差”工具来检验每对测量值变量,以便确定两个测量值变量是否趋向于同时变动,即,一个变量的较大值是否趋向于与另一个变量的较大值相关联(正相关);或者一个变量的较小值是否趋向于与另一个变量的较大值相关联(负相关);或者两个变量中的值趋向于互不关联(协方差近似于零)。
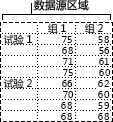
“描述统计”分析工具用于生成数据源区域中数据的单变量统计分析报表,提供有关数据趋中性和易变性的信息。
“指数平滑”分析工具根据前期预测导出新预测值,并修正前期预测值的误差。 此工具使用平滑常数 a,其大小决定了本次预测对前期预测误差的反馈程度。
注意: 0.2 到 0.3 之间的值是合理的平滑常数。 这些数值表明,由于前期预测值的误差,当前预测应调整 20% 到 30%。 较大的常数可产生较快的响应,但将产生不稳定的结果。 较小的常数将导致预测值长期的延迟。
“F-检验 双样本方差”分析工具通过双样本 F-检验对两个样本总体的方差进行比较。
例如,您可对一次游泳比赛中两个队伍各自的时间样本使用 F-检验工具。 该工具提供的检验结果,是以零假设为条件,即两个样本来自具有相同方差的分布,而不是以基础分布中方差不相等的备择假设为条件。
该工具计算 F-统计(或 F-比值)的 f 值。 接近 1 的 f 值证明基础样本总体方差相等。 在输出表格中,如果 f < 1,“P(F <= f) 单尾”返回当样本总体方差相等时观测到 F-统计值小于 f 的概率,而“F 单尾临界值”返回选定显著性水平 (Alpha) 的小于 1 的临界值。 如果 f > 1,“P(F <= f) 单尾”返回当样本总体方差相等时观测到 F-统计值大于 f 的概率,而“F 单尾临界值”提供 Alpha 的大于 1 的临界值。
“傅立叶分析”分析工具可以解决线性系统问题,并通过使用快速傅立叶变换 (FFT) 方法转换数据来分析周期性数据。 此工具也支持逆变换,对变换后的数据进行逆变换可返回原始数据。

“移动平均”分析工具可以基于特定的过去几个时期中变量的平均值,设计预测期间的值。 移动平均值提供了由所有历史数据的简单平均值所代表的趋势信息。 使用此工具可以预测销售量、库存或其他趋势。 每个预测值以下列计算公式为基础。
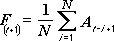
其中:
-
N 为进行移动平均包含的过去期间的个数
-
A j 为期间 j 的实际值
-
F j 为期间 j 的预测值
“随机数发生器”分析工具可用几个分布中的一个产生的独立随机数字来填充某个区域。 可以通过概率分布来表示样本总体中的主体特征。 例如,可以使用正态分布来表示人体身高的总体特征,或者使用两项可能结果的伯努利分布来表示掷币实验结果的总体特征。
“排位与百分比排位”分析工具可以产生一个数据表,在其中包含数据集中各个数值的顺序排位和百分比排位。 该工具用来分析数据集中各数值间的相对位置关系。 该工具使用工作表函数 RANK.EQ和 PERCENTRANK.INC。 如果希望考虑重复值,请使用 RANK.EQ 函数,此函数将重复值视作具备相同排位;或者使用 RANK.AVG 函数,此函数对重复值返回平均排位。
回归分析工具通过对一组观察值使用“最小二乘法”直线拟合来执行线性回归分析。 本工具可用来分析单个因变量是如何受一个或多个自变量影响的。 例如,分析某个运动员的运动成绩与一系列统计因素的关系,如年龄、身高和体重等。 根据一组成绩数据,您可确定这三个因素分别在运动成绩测量中所占的比重;然后使用该结果对尚未测量的运动员的成绩作出预测。
回归工具使用工作表函数 LINEST。
抽样分析工具以数据源区域为样本总体,并为此样本总体创建一个样本。 当总体太大而不能进行处理或绘制时,可以选用具有代表性的样本。 如果确认数据源区域中的数据是周期性的,还可创建一个样本,其中仅包含一个周期中特定时间段的数值。 例如,如果数据源区域包含季度销售量数据,以四为周期性速率进行取样,将在输出区域生成与数据源区域中相同季度的数值。
“双样本 t-检验”分析工具基于每个样本检验样本总体平均值的等同性。 这三个工具分别使用不同的假设:样本总体方差相等;样本总体方差不相等;两个样本代表同一主体处理前后的观察值。
对于以下所有三个工具,t-统计值 t 在输出表中计算并显示为“t Stat”。 数据决定了 t 是负值还是非负值。 假设基于相等的基础总体平均值,如果 t < 0,则“P(T <= t) 单尾”返回 t-统计的观察值比 t 更趋向负值的概率。 如果 t >=0,则“P(T <= t) 单尾”返回 t-统计的观察值比 t 更趋向正值的概率。 “t 单尾临界值”返回截止值,这样,t-统计的观察值将大于或等于“t 单尾临界值”的概率就为 Alpha。
“P(T <= t) 双尾”返回 t-统计的观测值绝对值大于 t 的概率。 “P 双尾临界值”返回截止值,这样,t-统计的观测值绝对值大于“P 双尾临界值”的概率就为 Alpha。
t-检验:成对双样本平均值
当样本中存在自然配对的观察值时(例如,对一个样本组在实验前后进行了两次检验), 可以使用此成对检验。 此分析工具及其公式可以进行成对双样本学生的 t-检验,以确定取自处理前后的观察值是否来自具有相同总体平均值的分布。 此 t-检验窗体并未假设两个总体的方差是相等的。
注意: 由此工具生成的结果中包含有合并方差,亦即数据相对于平均值的离散值的累积测量值,可以由下面的公式得到:
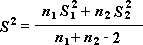
t-检验:双样本等方差假设
本分析工具可进行双样本学生 t-检验。 此 t-检验窗体先假设两个数据集取自具有相同方差的分布。 故也称作同方差 t-检验。 可以使用此 t-检验来确定两个样本是否可能来自具有相同总体平均值的分布。
t-检验:双样本异方差假设
本分析工具可进行双样本学生 t-检验。 此 t-检验窗体先假设两个数据集取自具有不同方差的分布。 故也称作异方差 t-检验。 如同上面的“等方差”情况,可以使用此 t-检验来确定两个样本是否可能来自具有相同总体平均值的分布。 当两个样本中有截然不同的对象时,可使用此检验。 当具有唯一的一组对象以及代表每个对象在处理前后的测量值的两个样本时,则应使用下面所描述的成对检验。
用于确定统计值 t 的公式如下。
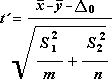
下列公式可用于计算自由度 df。 因为计算结果一般不是整数,所以 df 的值被舍入为最接近的整数,以便从 t 表中获得临界值。 因为使用非整数 df 值有可能计算 T.TEST值,所以 Excel 工作表函数 T.TEST 使用未进行舍入的 df 计算值。 由于这些决定自由度的不同方式,T.TEST 函数和此 t-检验工具的结果在“异方差”情况中将不同。
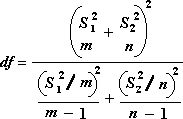
“z-检验:双样本平均值”分析工具可对具有已知方差的双样本平均值进行 z-检验。 此工具用于检验两个总体平均值之间不存在差异的零假设,而不是单方或双方的备择假设。 如果方差未知,则应该使用工作表函数 Z.TEST。
当使用“z-检验”工具时,应该仔细理解输出。 当总体平均值之间没有差别时,“P(Z <= z) 单尾”是 P(Z >= ABS(z)),即与 z 观察值沿着相同的方向远离 0 的 z 值的概率。 当总体平均值之间没有差异时,“P(Z <= z) 双尾”是 P(Z >= ABS(z) 或 Z <= -ABS(z)),即沿着任何方向(而非与观察到的 z 值的方向一致)远离 0 的 z 值的概率。 双尾结果只是单尾结果乘以 2。 z-检验工具还可用于当两个总体平均值之间的差异具有特定的非零值的零假设的情况。 例如,可以使用此检验来确定两种汽车型号之间的性能差异情况。
需要更多帮助吗?
可随时在 Excel 技术社区中咨询专家或在社区中获取支持。







