Lưu ý: Chúng tôi muốn cung cấp cho bạn nội dung trợ giúp mới nhất ở chính ngôn ngữ của bạn, nhanh nhất có thể. Trang này được dịch tự động nên có thể chứa các lỗi về ngữ pháp hoặc nội dung không chính xác. Mục đích của chúng tôi là khiến nội dung này trở nên hữu ích với bạn. Vui lòng cho chúng tôi biết ở cuối trang này rằng thông tin có hữu ích với bạn không? Dưới đây là bài viết bằng Tiếng Anh để bạn tham khảo dễ hơn.
Bài viết này đề cập đến việc dùng bộ giải, hãy thêm trong Microsoft Excel chương trình bạn có thể dùng cho phân tích what-if, để xác định một tập hợp các sản phẩm tối ưu.
Làm thế nào tôi có thể xác định trộn sản phẩm hàng tháng tối đa hóa lợi nhuận?
Các công ty thường cần phải xác định số lượng mỗi sản phẩm để tạo ra trên cơ sở hàng tháng. Trong biểu mẫu đơn giản nhất của nó, sản phẩm kết hợp các vấn đề liên quan đến làm thế nào để xác định giá trị của mỗi sản phẩm sẽ được tạo trong một tháng để tối đa hóa lợi nhuận. Sản phẩm hợp thường phải tuân theo để giới hạn sau đây:
-
Sản phẩm hợp không thể sử dụng tài nguyên khác hơn sẵn dùng.
-
Không có một yêu cầu giới hạn cho từng sản phẩm. Chúng tôi không thể tạo ra nhiều sản phẩm trong một tháng hơn ra yêu cầu, vì sản xuất quá mức là lãng phí (ví dụ, một ma túy dễ hỏng).
Hãy giải quyết ngay ví dụ sau đây về vấn đề hợp sản phẩm. Bạn có thể tìm thấy giải pháp cho vấn đề này trong tệp Prodmix.xlsx, Hiển thị trong hình 27-1.
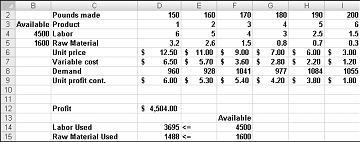
Giả sử chúng tôi làm việc cho một công ty ma túy cho sáu sản phẩm khác nhau ở cây của họ. Sản xuất của từng sản phẩm này yêu cầu lao động và nguyên liệu. Chỉ cho hàng 4 trong hình 27-1 giờ lao động cần thiết để tạo ra một thăng từng sản phẩm và hàng 5 cân nguyên liệu cần thiết để tạo ra một thăng từng sản phẩm. Ví dụ: sản xuất một thăng sản phẩm 1 yêu cầu sáu giờ lao động và 3.2 £ của nguyên liệu. Đối với mỗi ma túy, giá trên mỗi thăng được cung cấp trong hàng 6, chi phí đơn vị mỗi thăng được cung cấp trong hàng 7 và đóng góp lợi nhuận cho mỗi thăng được cung cấp ở hàng 9. Ví dụ, sản phẩm 2 bán $11,00 cho mỗi thăng, làm phát sinh phí đơn vị của $5,70 cho mỗi thăng và đóng góp $5,30 lợi nhuận cho mỗi thăng. Yêu cầu của tháng cho mỗi ma túy được cung cấp trong hàng 8. Ví dụ, yêu cầu về sản phẩm 3 là 1041 £. Tháng này, 4500 giờ lao động và 1600 £ của nguyên liệu sẵn dùng. Làm thế nào có thể công ty này tối đa hóa lợi nhuận hàng tháng?
Nếu chúng tôi biết điều gì về Excel bộ giải, chúng tôi sẽ tấn công vấn đề này bằng xây dựng một trang tính để theo dõi các cách dùng lợi nhuận và tài nguyên liên kết với sản phẩm hợp. Sau đó chúng ta dùng bản dùng thử và lỗi để thay đổi tập hợp sản phẩm để tối ưu hóa lợi nhuận mà không dùng nhiều lao động hoặc nguyên liệu hơn sẵn có và không có bất kỳ ma túy vượt quá yêu cầu sản xuất. Chúng tôi dùng bộ giải trong quy trình này chỉ ở giai đoạn dùng thử và lỗi. Cơ bản, bộ giải là một công cụ tối ưu hóa hoàn hảo sẽ tìm kiếm bản dùng thử và lỗi.
Một khóa để giải quyết vấn đề hợp sản phẩm là một cách hiệu quả tính toán sử dụng tài nguyên và lợi nhuận liên kết với bất kỳ kết hợp các sản phẩm đã cho. Một công cụ quan trọng mà chúng tôi có thể dùng để thực hiện tính toán này là hàm SUMPRODUCT. Hàm SUMPRODUCT nhân các giá trị tương ứng trong phạm vi ô và trả về tổng của các giá trị này. Mỗi phạm vi ô được dùng trong một đánh giá hàm SUMPRODUCT phải có cùng kích thước, mà ngụ ý mà bạn có thể dùng SUMPRODUCT với hai hàng hoặc hai cột, nhưng không có một cột và một hàng.
Làm ví dụ về cách chúng tôi có thể sử dụng hàm SUMPRODUCT trong sản phẩm của chúng tôi trộn ví dụ, hãy thử để tính sử dụng tài nguyên của chúng tôi. Cách dùng lao động của chúng tôi được tính toán bằng
(Lao động sử dụng cho mỗi thăng ma túy 1) *(Drug 1 pounds produced) + (lao động sử dụng cho mỗi thăng ma túy 2) * (ma túy 2 cân sản xuất) +... (Lao động sử dụng cho mỗi thăng ma túy 6) * (ma túy 6 cân sản xuất)
Chúng tôi có thể tính lao động sử dụng nhiều tedious luôn là D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4. Tương tự, sử dụng nguyên liệu có thể được tính cho chúng dưới dạng D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + I2 * I5. Tuy nhiên, nhập các công thức trong một trang tính dành cho sản phẩm sáu là tốn. Giả sử sẽ mất bao lâu nếu bạn đang làm việc với một công ty sản xuất, ví dụ, các sản phẩm 50 tại cây của họ. Một cách dễ dàng hơn nhiều để tính lao động và cách dùng nguyên liệu là sao chép từ D14 D15 công thức SUMPRODUCT($D$2:$I$2,D4:I4). Công thức này tính D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4 (là cách dùng lao động của chúng tôi) nhưng dễ dàng hơn để nhập! Lưu ý rằng tôi sử dụng dấu $ với phạm vi D2:I2 để khi tôi sao chép công thức tôi vẫn chụp hợp sản phẩm từ hàng 2. Công thức trong ô D15 tính nguyên liệu sử dụng.
Một cách tương tự, lợi nhuận của chúng tôi được xác định bởi
(Ma túy lợi nhuận 1 cho mỗi thăng) * (sản xuất bảng ma túy 1) + (ma túy 2 lợi nhuận cho mỗi thăng) * (ma túy 2 cân sản xuất) +... (Ma túy 6 lợi nhuận cho mỗi thăng) * (ma túy 6 cân sản xuất)
Lợi nhuận dễ dàng được tính toán trong ô D12 với công thức SUMPRODUCT(D9:I9,$D$2:$I$2).
Bây giờ chúng tôi có thể xác định ba cấu phần của tập hợp sản phẩm của chúng tôi tìm hiểu mô hình.
-
Ô đích.Mục tiêu của chúng tôi là tối đa hóa lợi nhuận (tính cho chúng trong ô D12).
-
Thay đổi ô.Số lượng cân sản xuất của từng sản phẩm (được liệt kê trong phạm vi ô D2:I2)
-
Ràng buộc. Chúng tôi có ràng buộc thao tác sau:
-
Không sử dụng nhiều lao động hoặc nguyên liệu hơn sẵn dùng. Có nghĩa là, các giá trị trong ô D14:D15 (tài nguyên được sử dụng) phải nhỏ hơn hoặc bằng các giá trị trong ô F14:F15 (tài nguyên sẵn dùng).
-
Không tạo ra nhiều trong một ma túy hơn trong yêu cầu. Có nghĩa là, các giá trị trong ô D2:I2 (bảng sản xuất của mỗi ma túy) phải nhỏ hơn hoặc bằng yêu cầu cho mỗi ma túy (được liệt kê trong ô D8:I8).
-
Chúng tôi không thể tạo ra một số âm ma túy bất kỳ.
-
Tôi sẽ hướng dẫn bạn cách để nhập ô đích, thay đổi ô, và ràng buộc vào bộ giải. Sau đó tất cả bạn cần làm là bấm vào nút giải quyết để tìm một tập hợp sản phẩm tối đa hóa lợi nhuận!
Để bắt đầu, bấm vào tab dữ liệu, trong nhóm phân tích, bấm bộ giải.
Lưu ý: Như được giải thích trong chương 26, "An giới thiệu để tối ưu hóa với Excel bộ giải," bộ giải được cài đặt bằng cách bấm nút Microsoft Office, sau đó tùy chọn Excel, theo sau là bổ trợ. Trong danh sách quản lý, bấm bổ trợ Excel, hãy chọn hộp bổ trợ bộ giải và sau đó bấm OK.
Hộp thoại tham số bộ giải sẽ xuất hiện, như minh họa trong hình 27-2.
Bấm vào hộp đặt ô đích và sau đó chọn ô lợi nhuận của chúng tôi (ô D12). Bấm vào hộp bằng cách thay đổi ô và sau đó trỏ đến phạm vi D2:I2, chứa £ sản xuất của mỗi ma túy. Hộp thoại bây giờ sẽ hiển thị hình 27-3.
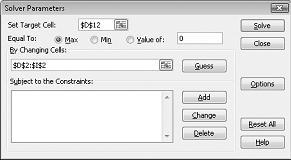
Chúng tôi đã sẵn sàng thêm ràng buộc vào mô hình. Bấm vào nút Thêm. Bạn sẽ thấy hộp thoại thêm ràng buộc, Hiển thị trong hình 27-4.
Để thêm ràng buộc sử dụng tài nguyên, hãy bấm vào hộp tham chiếu ô, sau đó chọn phạm vi D14:D15. Chọn < = từ danh sách tên đệm. Bấm vào hộp ràng buộc, sau đó chọn phạm vi ô F14:F15. Hộp thoại thêm ràng buộc bây giờ sẽ trông giống như hình 27-5.
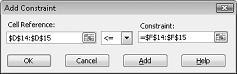
Chúng tôi phải đảm bảo rằng khi bộ giải tìm cách các giá trị khác nhau cho các thay đổi các ô, bất kỳ tổ hợp chỉ thỏa mãn cả hai D14< = F14 (lao động sử dụng là nhỏ hơn hoặc bằng lao động sẵn có) và D15< = F15 (nguyên liệu sử dụng là nhỏ hơn hoặc bằng nguyên liệu sẵn dùng) sẽ được coi là. Bấm Thêm để nhập ràng buộc yêu cầu. Điền trong hộp thoại thêm ràng buộc như minh họa trong hình 27-6.
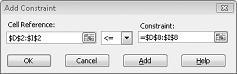
Thêm ràng buộc những đảm bảo rằng khi bộ giải tìm cách kết hợp khác nhau cho các giá trị ô thay đổi, chỉ những tổ hợp thỏa mãn các tham số sau đây sẽ được coi là:
-
D2< = D8 (giá trị sản xuất của ma túy 1 là nhỏ hơn hoặc bằng nhu cầu về ma túy 1)
-
E2< = E8 (lượng sản xuất của ma túy 2 là nhỏ hơn hoặc bằng nhu cầu về ma túy 2)
-
F2< = F8 (giá trị sản xuất của ma túy 3 đã thực hiện là nhỏ hơn hoặc bằng nhu cầu về ma túy 3)
-
G2< = G8 (giá trị sản xuất ma túy 4 đã thực hiện là nhỏ hơn hoặc bằng nhu cầu về ma túy 4)
-
H2< = H8 (giá trị sản xuất của ma túy 5 thực hiện là nhỏ hơn hoặc bằng nhu cầu về ma túy 5)
-
I2< = I8 (giá trị sản xuất của ma túy 6 đã thực hiện là nhỏ hơn hoặc bằng nhu cầu về ma túy 6)
Bấm OK trong hộp thoại thêm ràng buộc. Cửa sổ bộ giải sẽ trông giống như hình 27-7.
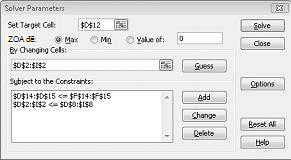
Chúng tôi nhập ràng buộc thay đổi ô phải là không âm trong hộp thoại tùy chọn bộ giải. Bấm nút tùy chọn trong hộp thoại tham số bộ giải. Kiểm tra hộp giả định tuyến tính mô hình và hộp giả định không âm, như minh họa trong hình 27-8 trên trang tiếp theo. Bấm OK.
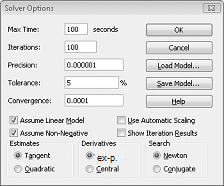
Kiểm tra xem như không phải âm hộp đảm bảo bộ giải xem xét chỉ tổ hợp các thay đổi ô trong đó mỗi ô thay đổi giả định một giá trị không âm. Chúng tôi kiểm tra hộp giả định tuyến tính mô vì sản phẩm trộn vấn đề là một kiểu đặc biệt của vấn đề bộ giải được gọi là một mô hình tuyến tính. Cơ bản, mô hình bộ giải được tuyến tính bên dưới các điều kiện sau đây:
-
Ô đích được tính cho chúng bằng cách thêm các số hạng của biểu mẫu với nhau (thay đổi cell)*(constant).
-
Ràng buộc mỗi thỏa mãn tối "yêu cầu tuyến tính mô hình." Điều này nghĩa là ràng buộc mỗi được đánh giá bằng cách thêm các số hạng của biểu mẫu với nhau (thay đổi cell)*(constant) và so sánh tính tổng cho một hằng số.
Tại sao được giải quyết vấn đề này tuyến tính? Chúng tôi ô đích (lợi nhuận) được tính cho chúng dưới dạng
(Ma túy lợi nhuận 1 cho mỗi thăng) * (sản xuất bảng ma túy 1) + (ma túy 2 lợi nhuận cho mỗi thăng) * (ma túy 2 cân sản xuất) +... (Ma túy 6 lợi nhuận cho mỗi thăng) * (ma túy 6 cân sản xuất)
Tính toán này theo một mẫu hình trong đó giá trị của ô đích được lấy bằng cách thêm thuật ngữ biểu mẫu với nhau (thay đổi cell)*(constant).
Ràng buộc lao động của chúng tôi được đánh giá bằng cách so sánh giá trị phái sinh từ (lao động sử dụng cho mỗi thăng ma túy 1) * (sản xuất bảng ma túy 1) + (lao động sử dụng cho mỗi thăng ma túy 2) *(Drug 2 pounds produced) +... (Lao động chúng tôied cho mỗi thăng ma túy 6) * (ma túy 6 cân sản xuất) để lao động sẵn dùng.
Do đó, ràng buộc lao động được đánh giá bằng cách thêm các số hạng của biểu mẫu với nhau (thay đổi cell)*(constant) và so sánh tính tổng cho một hằng số. Ràng buộc lao động và ràng buộc nguyên liệu thỏa mãn yêu cầu tuyến tính mô hình.
Giới hạn của chúng tôi yêu cầu thực hiện biểu mẫu
(Ma túy 1 sản xuất) < = (ma túy 1 yêu cầu) (ma túy 2 sản xuất) < = (ma túy 2 yêu cầu) • (ma túy 6 sản xuất) < = (ma túy 6 yêu cầu)
Ràng buộc yêu cầu mỗi cũng đáp ứng yêu cầu tuyến tính mô hình, bởi vì mỗi được đánh giá bằng cách thêm các số hạng của biểu mẫu với nhau (thay đổi cell)*(constant) và so sánh tính tổng cho một hằng số.
Có hiển thị mô hình kết hợp sản phẩm của chúng tôi là một mô hình tuyến tính, tại sao nên chúng tôi xử lý?
-
Nếu một mô hình bộ giải được tuyến tính và chúng tôi chọn giả định tuyến tính mô hình, bộ giải được bảo đảm để tìm giải pháp tối ưu vào mô hình bộ giải. Nếu một mô hình bộ giải không phải là tuyến tính, bộ giải có thể hoặc không có thể tìm thấy giải pháp tối ưu.
-
Nếu một mô hình bộ giải được tuyến tính và chúng tôi chọn giả định tuyến tính mô hình, bộ giải sử dụng một thuật toán rất có hiệu quả (phương pháp simplex) để tìm giải pháp tối ưu vào mô hình. Nếu một mô hình bộ giải được tuyến tính và chúng tôi không chọn giả định tuyến tính mô hình, bộ giải sử dụng một thuật toán không hiệu quả rất (phương pháp GRG2) và có thể khó tìm giải pháp tối ưu vào mô hình.
Sau khi bấm vào OK trong hộp thoại tùy chọn bộ giải, chúng tôi trở lại vào chính hộp thoại bộ giải, Hiển thị phiên bản cũ hơn trong hình 27-7. Khi chúng tôi bấm giải quyết, bộ giải tính giải pháp tối ưu (nếu một tồn tại) cho mô hình kết hợp sản phẩm của chúng tôi. Khi tôi đã nêu trong chương 26, giải pháp tối ưu vào mô hình kết hợp sản phẩm sẽ một bộ các thay đổi giá trị ô (bảng sản xuất của mỗi ma túy) tối đa hóa lợi nhuận đối với tập hợp các giải pháp khả thi tất cả. Một lần nữa, giải pháp khả thi là một tập hợp các thay đổi giá trị ô thỏa mãn tất cả ràng buộc. Các giá trị ô thay đổi hiển thị trong hình 27-9 là giải pháp nào có thể vì tất cả các mức sản xuất được không âm, cấp độ sản xuất không vượt quá yêu cầu và sử dụng tài nguyên không vượt quá tài nguyên sẵn dùng.
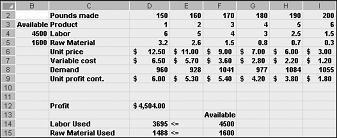
Các giá trị ô thay đổi hiển thị trong hình 27-10 trên trang tiếp theo đại diện cho giải infeasible giải pháp vì các lý do sau đây:
-
Chúng tôi đã tạo ra nhiều ma túy 5 hơn yêu cầu cho nó.
-
Chúng tôi sử dụng nhiều lao động hơn những gì có sẵn.
-
Chúng tôi sử dụng nhiều nguyên liệu hơn những gì có sẵn.
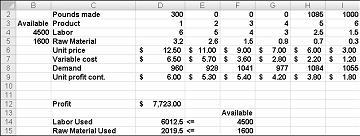
Sau khi bấm giải quyết, nhanh chóng bộ giải tìm giải pháp tối ưu Hiển thị trong hình 27-11. Bạn cần phải chọn giữ giải pháp bộ giải để giữ nguyên các giải pháp tối ưu việc theo giá trị trong trang tính.
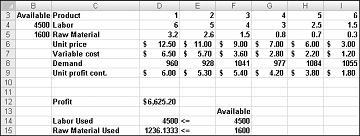
Công ty ma túy của chúng tôi có thể tối đa hóa lợi nhuận hàng tháng ở cấp độ $6,625.20 bằng sản xuất 596.67 £ của ma túy 4, 1084 £ của ma túy 5 và không có thuốc khác! Chúng tôi không thể xác định nếu chúng tôi có thể đạt được tối đa lợi nhuận của $6,625.20 theo nhiều cách khác. Tất cả chúng tôi có thể chắc chắn về là rằng với các giới hạn tài nguyên và yêu cầu, không có cách nào để thực hiện nhiều hơn $6,627.20 tháng này.
Giả sử rằng yêu cầu cho mỗi sản phẩm phải đáp ứng. (Hãy xem trang tính Không có giải pháp khả thi trong tệp Prodmix.xlsx.) Chúng tôi rồi có thay đổi giới hạn của chúng tôi yêu cầu từ D2:I2< = D8:I8 để D2:I2> = D8:I8. Để thực hiện điều này, mở bộ giải, hãy chọn D2:I2< = D8:I8 ràng buộc, và sau đó bấm thay đổi. Hộp thoại thay đổi ràng buộc, Hiển thị trong hình 27-12, xuất hiện.
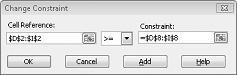
Chọn > =, sau đó bấm OK. Chúng tôi đã đảm bảo bộ giải sẽ cân nhắc việc thay đổi chỉ giá trị ô thỏa mãn tất cả các nhu cầu. Khi bạn bấm giải quyết, bạn sẽ thấy thông báo "Bộ giải không thể tìm thấy giải pháp khả thi." Thông báo này có nghĩa là chúng tôi đã thực hiện nhầm trong mô hình của chúng tôi, nhưng thay vì mà có giới hạn tài nguyên của chúng tôi, chúng tôi không thể đáp ứng các yêu cầu cho tất cả sản phẩm. Bộ giải chỉ cần cho chúng tôi nếu chúng tôi muốn đáp ứng các yêu cầu cho từng sản phẩm, chúng tôi cần để thêm nhiều lao động, thêm nguyên liệu hoặc nhiều trong cả hai.
Hãy cùng xem điều gì xảy ra nếu chúng tôi cho phép các yêu cầu không giới hạn cho từng sản phẩm và chúng tôi cho phép âm lượng được sản xuất của mỗi ma túy. (Bạn có thể xem giải quyết vấn đề này trên trang tính Đặt giá trị thực hiện không hội tụ trong tệp Prodmix.xlsx.) Để tìm giải pháp tối ưu cho tình huống này, mở bộ giải, bấm nút tùy chọn và xóa hộp giả định không âm. Trong hộp thoại tham số bộ giải, chọn ràng buộc yêu cầu D2:I2< = D8:I8 và sau đó bấm Xóa để loại bỏ ràng buộc. Khi bạn bấm giải quyết, bộ giải trả về thông báo "Đặt giá trị ô không hội tụ." Thông báo này rằng nếu ô đích là để phóng to (như trong ví dụ của chúng tôi), có nghĩa là các giải pháp khả thi với giá trị ô đích tự ý lớn. (Nếu ô đích là được thu nhỏ, thông báo "Đặt ô giá trị thực hiện không hội tụ" có nghĩa là các giải pháp khả thi với giá trị ô đích tự ý small.) Trong tình huống của chúng tôi, bằng cách cho phép âm sản xuất của ma túy, chúng ta hiệu lực "tạo" tài nguyên có thể được dùng để tạo ra số lượng lớn tự ý ma túy khác. Điều này được cung cấp của chúng tôi yêu cầu không giới hạn, cho phép chúng tôi để thực hiện không giới hạn lợi nhuận. Trong tình huống thực, chúng tôi không thể thực hiện một số lượng vô tiền. Nói tóm lại, nếu bạn thấy "Đặt giá trị thực hiện không hội tụ", mô hình của bạn có lỗi.
-
Giả sử công ty ma túy của chúng tôi có thể mua đến 500 giờ lao động $1 / giờ hơn chi phí lao động hiện tại. Làm thế nào chúng tôi có thể tối đa hóa lợi nhuận?
-
Ở một chip sản xuất cây, bốn kỹ thuật (A, B, C và D) sản ba (sản phẩm 1, 2 và 3). Tháng này, nhà sản xuất chip có thể bán 80 đơn vị của sản phẩm 1, 50 đơn vị của sản phẩm 2, và lúc nhất 50 đơn vị của sản phẩm 3. Kỹ thuật A có thể thực hiện chỉ có sản phẩm 1 và 3. Kỹ thuật B có thể thực hiện chỉ có sản phẩm 1 và 2. Kỹ thuật C có thể thực hiện chỉ sản phẩm 3. Kỹ thuật D có thể thực hiện chỉ sản phẩm 2. Cho mỗi đơn vị sản xuất, các sản phẩm đóng góp lợi nhuận sau đây: sản phẩm 1, $6; Sản phẩm 2, $7; và sản phẩm 3, $10. Thời gian (trong giờ) kỹ thuật mỗi cần sản xuất một như sau:
Sản phẩm
Kỹ thuật A
Kỹ thuật B
Kỹ thuật C
Kỹ thuật D
1
2
2,5
Không thể thực hiện
Không thể thực hiện
2
Không thể thực hiện
3
Không thể thực hiện
3,5
3
3
Không thể thực hiện
4
Không thể thực hiện
-
Kỹ thuật mỗi có thể làm việc đến 120 giờ mỗi tháng. Làm thế nào có thể nhà sản xuất chip tối đa hóa lợi nhuận hàng tháng? Giả định một số thập phân của đơn vị có thể được sản xuất.
-
Máy tính sản xuất cây cho chuột, Bàn phím và cần điều khiển trò chơi video. Lợi nhuận cho mỗi đơn vị, trên mỗi đơn vị lao động sử dụng, hàng tháng yêu cầu và trên mỗi đơn vị thời gian máy sử dụng được cung cấp trong bảng sau đây:
Chuột
Bàn phím
Cần điều khiển
Lợi nhuận/đơn vị
$8
$11
$9
Cách dùng lao động/đơn vị
.2 giờ
.3 giờ
.24 giờ
Máy thời gian/đơn vị
.04 giờ
.055 giờ
.04 giờ
Yêu cầu hàng tháng
15.000
27.000
11.000
-
Mỗi tháng, tổng cộng 13.000 lao động giờ và 3000 giờ của máy thời gian sẵn dùng. Làm thế nào có thể phóng to nhà sản xuất của nó đóng góp lợi nhuận hàng tháng từ cây?
-
Giải quyết của chúng tôi ví dụ ma túy giả định một yêu cầu tối thiểu 200 đơn vị cho mỗi ma túy phải đáp ứng.
-
Jason làm cho hình kim cương vòng, dây và tai. Anh ấy muốn làm việc tối đa 160 giờ mỗi tháng. Anh ấy có 800 ounce hình thoi. Lợi nhuận, lao động thời gian và ounce hình thoi cần thiết để tạo ra từng sản phẩm được đưa ra dưới đây. Nếu yêu cầu cho từng sản phẩm không giới hạn, làm thế nào có thể Jason tối đa hóa lợi nhuận của mình?
Sản phẩm
Lợi nhuận đơn vị
Giờ lao động mỗi đơn vị
Ounce hình thoi mỗi đơn vị
Vòng tay
$300
.35
1.2
Vòng
200 $
.15
.75
Tai
$100
,05
.5










