Trả về phân bố Poisson. Một ứng dụng thường gặp của phân bố Poisson là để dự đoán số sự kiện trong một thời gian cụ thể, chẳng hạn như số xe tới một trạm thu phí trong 1 phút.
Cú pháp
POISSON.DIST(x,mean,cumulative)
Cú pháp hàm POISSON.DIST có các đối số sau đây:
-
X Bắt buộc. Số sự kiện.
-
Mean Bắt buộc. Giá trị dạng số ước tính.
-
Cumulative Bắt buộc. Giá trị lô-gic xác định dạng thức của phân bố xác suất được trả về. Nếu cumulative là TRUE, thì hàm POISSON.DIST trả về xác xuất Poisson lũy tích mà một số sự kiện ngẫu nhiên sẽ xảy ra từ không đến x, bao gồm cả không và x; nếu FALSE, nó trả về hàm khối xác xuất Poission mà số sự kiện xảy ra sẽ chính xác là x.
Chú thích
-
Nếu x không phải là số nguyên thì nó bị cắt cụt.
-
Nếu x hoặc giá trị trung độ không có dạng số, hàm POISSON.DIST trả về giá trị lỗi #VALUE! .
-
Nếu x < 0, POISSON.DIST trả về giá trị lỗi #NUM! .
-
Nếu giá trị trung độ < 0, hàm POISSON.DIST trả về giá trị lỗi #NUM! .
-
Hàm POISSON.DIST được tính toán như sau.
Với lũy tích = FALS:
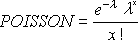
Với lũy tích = TRUE:
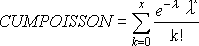
Ví dụ
Sao chép dữ liệu ví dụ trong bảng sau đây và dán vào ô A1 của một bảng tính Excel mới. Để các công thức hiển thị kết quả, hãy chọn chúng, nhấn F2 và sau đó nhấn Enter. Nếu cần, bạn có thể điều chỉnh độ rộng cột để xem toàn bộ dữ liệu.
|
Dữ liệu |
Mô tả |
|
|
2 |
Số sự kiện |
|
|
5 |
Giá trị trung độ dự kiến |
|
|
Công thức |
Mô tả |
K ết quả |
|
=POISSON.DIST(A2,A3,TRUE) |
Xác suất Poisson lũy tích với các đối số được xác định tại A2 và A3. |
0,124652 |
|
=POISSON.DIST(A2,A3,FALSE) |
Hàm khối xác suất Poisson với các đối số được xác định tại A2 và A3. |
0,084224 |










