Bu makalede, Microsoft Excel'de ZTEST işlevinin formül sözdizimi ve kullanımı açıklanmaktadır.
Bir z-testinin tek kuyruklu olasılık değerini verir. Hipotez olarak belirlenen bir μ0 popülasyon ortalamasında, ZTEST örnek ortalamasının veri kümesindeki (dizisindeki) gözlemlerin ortalamasından daha büyük olma olasılığını, başka bir deyişle, gözlemlenen örnek ortalamasını verir.
ZTEST'in iki kuyruklu bir olasılık değerini hesaplamak üzere bir formülde nasıl kullanılacağını öğrenmek için aşağıdaki "Notlar" bölümüne bakın.
Önemli: Bu işlevin yerini, daha iyi bir doğruluk sağlayabilecek ve adları kullanımlarını daha iyi yansıtan bir veya daha fazla yeni işlev almıştır. Geriye dönük uyumluluk açısından bu işlev halen kullanılabilir olmakla birlikte, Excel'in gelecek sürümlerinde bulunmayabileceğinden bundan sonra yeni işlevleri kullanmaya başlamayı düşünmelisiniz.
Yeni işlev hakkında daha fazla bilgi için bkz. Z.TEST işlevi.
Söz dizimi
ZTEST(dizi,x,[sigma])
ZTEST işlevinin söz diziminde aşağıdaki bağımsız değişkenler bulunur.
-
Dizi Gerekli. X'in test edileceği dizi veya veri aralığıdır.
-
X Gerekli. Sınanacak değerdir.
-
Sigma İsteğe bağlı. Popülasyon (bilinen) standart sapmasıdır. Belirtilmezse, örnekleme standart sapması kullanılır.
Notlar
-
Dizi boşsa, ZTEST işlevi #YOK hata değerini verir.
-
ZTEST, sigma atlanmadığında, aşağıdaki gibi hesaplanır:
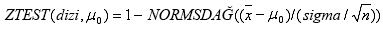
veya sigma atlandığında:

burada x, ORTALAMA(dizi) örnek ortalamasıdır; s ise, STDSAPMA(dizi) örnek standart sapmadır; n, BAĞ_DEĞ_SAY(dizi) örneğindeki gözlem sayısıdır.
-
ZTEST, temel popülasyon ortalaması μ0 olduğunda, örnek ortalamanın gözlenen ORTALAMA(dizi) değerinden daha büyük olma olasılığını temsil eder. Normal dağılımın simetrisinden, ORTALAMA(dizi) < μ0 ise, ZTEST 0,5'ten büyük bir değer verir.
-
Aşağıdaki Excel formülü, temel popülasyon ortalaması μ0 olduğunda, örnek ortalamanın ORTALAMA(dizi) formülüne göre μ0'dan (her iki yönde) daha ileride olma olasılığını (çift kuyruklu) hesaplamak için kullanılabilir:
=2 * MİN(ZTEST(dizi,μ0,sigma), 1 - ZTEST(dizi,μ0,sigma)).
Örnek
Aşağıdaki tabloda yer alan örnek verileri kopyalayın ve yeni bir Excel çalışma sayfasının A1 hücresine yapıştırın. Formüllerin sonuçları göstermesi için, bunları seçip F2 tuşuna basın ve sonra Enter tuşuna basın. Gerekirse, tüm verileri görmek için sütun genişliğini ayarlayabilirsiniz.
|
Veri |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Formül |
Açıklama (Sonuç) |
Sonuç |
|
=ZTEST(A2:A11,4) |
Yukarıdaki veri kümesinin, hipotez olarak alınan 4 (0,090574) popülasyon ortalamasında, z-testinin tek kuyruklu olasılık değeri |
0,090574 |
|
=2 * MİN(ZTEST(A2:A11,4), 1 - ZTEST(A2:A11,4)) |
Yukarıdaki veri kümesinin, hipotez olarak alınan 4 (0,181148) popülasyon ortalamasında, z-testinin çift kuyruklu olasılık değeri |
0,181148 |
|
=ZTEST(A2:A11,6) |
Yukarıdaki veri kümesinin, hipotez olarak alınan 6 (0,863043) popülasyon ortalamasında, z-testinin tek kuyruklu olasılık değeri |
0,863043 |
|
=2 * MİN(ZTEST(A2:A11,6), 1 - ZTEST(A2:A11,6)) |
Yukarıdaki veri kümesinin, hipotez olarak alınan 6 (0,273913) popülasyon ortalamasında, z-testinin çift kuyruklu olasılık değeri |
0,273913 |










