Poisson dağılımını verir. Poisson dağılımının yaygın bir uygulaması, bir dakika içinde köprü gişesine gelen otomobillerin sayısı gibi, belirli bir zamandaki olayların sayısını tahmin etmektir.
Söz Dizimi
POISSON.DAĞ(x,ortalama,kümülatif)
POISSON.DAĞ işlevinin söz diziminde aşağıdaki bağımsız değişkenler bulunur:
-
X Gerekli. Olay sayısıdır.
-
Ortalama Gerekli. beklenen sayısal değerdir.
-
Kümülatif Gerekli. Döndürülen olasılık dağılımının biçimini belirleyen mantıksal değer. Kümülatif TRUE ise POISSON. DAĞ, gerçekleşen rastgele olayların sayısının sıfır ile x (dahil) arasında olacağı kümülatif Poisson olasılığını verir; YANLIŞ ise, gerçekleşen olayların sayısının tam olarak x olacağı Poisson olasılık kütle işlevini döndürür.
Notlar
-
X tamsayı değilse ondalık kısmı atılır.
-
X veya ortalama sayısal değilse, POISSON.DAĞ işlevi#DEĞER! hata değeri verir.
-
X < 0 ise, POISSON.DAĞ #SAYI! hata değeri verir.
-
Ortalama < 0 ise, POISSON.DAĞ #SAYI! hata değeri verir.
-
POISSON.DAĞ aşağıdaki gibi hesaplanır.
Kümülatif = YANLIŞ:
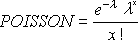
Kümülatif = DOĞRU:
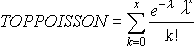
Örnek
Aşağıdaki tabloda yer alan örnek verileri kopyalayın ve yeni bir Excel çalışma sayfasının A1 hücresine yapıştırın. Formüllerin sonuçları göstermesi için, bunları seçip F2 tuşuna basın ve sonra Enter tuşuna basın. Gerekirse, tüm verileri görmek için sütun genişliğini ayarlayabilirsiniz.
|
Veri |
Açıklama |
|
|
2 |
Olay sayısı |
|
|
5 |
Beklenen ortalama |
|
|
Formül |
Açıklama |
S onuç |
|
=POISSON.DAĞ(A2,A3,DOĞRU) |
A2 ve A3'te belirtilen bağımsız değişkenlerle kümülatif Poisson olasılığı. |
0,124652 |
|
=POISSON.DAĞ(A2,A3,YANLIŞ) |
A2 ve A3'te belirtilen bağımsız değişkenlerle Poisson olasılığı kütle işlevi. |
0,084224 |










