GÜVENİLİRLİK.NORM işlevi

Açıklama

Güvenirlik aralığı, bir değer aralığıdır. Örnek ortalamanız olan x, bu aralığın ortasındadır ve aralık x ± GÜVENİLİRLİK.NORM şeklindedir. Örneğin, x e-posta ile sipariş edilen ürünlerin teslim sürelerinin örnek ortalaması ise x ± GÜVENİLİRLİK.NORM, bir popülasyon ortalaması aralığıdır. Herhangi bir popülasyon ortalaması için, µ0, bu aralıkta, µ0'dan x'ten daha ileride bir örnek ortalaması alma olasılığı alfa'dan daha büyüktür; herhangi bir popülasyon ortalaması için, µ0, bu aralığın dışında, µ0'dan x'ten daha ileride bir örnek ortalaması alma olasılığı alfa'dan daha küçüktür. Başka bir deyişle, standart_sapma x'i ve popülasyon ortalamasının µ0 olduğunu savunan hipotezin alfa anlam düzeyinde iki kuyruklu bir sınama oluşturma boyutunu kullandığımızı varsayalım. Bu durumda, µ0 güvenirlik aralığında ise bu hipotez reddedilmez, µ0 güvenirlik aralığında ise bu hipotez reddedilir. Güvenirlik aralığı 1 - alfa olasılığın (bir sonraki paketimizin güvenirlik aralığındaki bir teslim süresinde teslim edilmesi) olduğu anlamını çıkarmamıza izin vermez.

Söz Dizimi

GÜVENİLİRLİK.NORM(alfa,standart_sapma,boyut)

GÜVENİLİRLİK.NORM işlevinin söz diziminde aşağıdaki bağımsız değişkenler bulunur:

• Alfa     Gerekli. Güvenirlik düzeyini hesaplamak için kullanılan belirleyici düzeydir. Güvenirlik düzeyi, %100*(1 - alfa)'ya eşittir; veya başka bir deyişle 0,05 düzeyindeki bir alfa, yüzde 95 güvenirlik düzeyi belirtir.

• Standart_sapma     Gerekli. Veri aralığının popülasyon standart sapmasıdır ve bilindiği varsayılır.

• Boyut     Gerekli. Örnek boyutudur.

Notlar

• Herhangi bir bağımsız değişken sayısal değilse, GÜVENİLİRLİK.NORM, #DEĞER! hata değerini verir.

• Alfa ≤ 0'sa veya alfa ≥ 1'se, GÜVENİLİRLİK.NORM, #SAYI! hata değerini verir.

• Standart_sapma ≤ 0'sa, GÜVENİLİRLİK.NORM, #SAYI! hata değerini verir.

• Boyut, tamsayı değilse, fazlalıkları atılır.

• Boyut < 1'se, GÜVENİLİRLİK.NORM, #SAYI! hata değerini verir.

• Alfanın 0,05'e eşit olduğunu varsayarsak, standart normal eğrinin altındaki (1 - alfa)ya veya yüzde 95'e eşit olan alanı hesaplamamız gerekir. Bu değer, ± 1,96'dır. Öyleyse, GÜVENİRLİK aralığı:

  

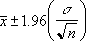
Örnek

Aşağıdaki tabloda yer alan örnek verileri kopyalayın ve yeni bir Excel çalışma sayfasının A1 hücresine yapıştırın. Formüllerin sonuçları göstermesi için, bunları seçip F2 tuşuna basın ve sonra Enter tuşuna basın. Gerekirse, tüm verileri görmek için sütun genişliğini ayarlayabilirsiniz.