Not: En güncel yardım içeriklerini, mümkün olduğunca hızlı biçimde kendi dilinizde size sunmak için çalışıyoruz. Bu sayfanın çevirisi otomasyon aracılığıyla yapılmıştır ve bu nedenle hatalı veya yanlış dil bilgisi kullanımları içerebilir. Amacımız, bu içeriğin sizin için faydalı olabilmesini sağlamaktır. Buradaki bilgilerin faydalı olup olmadığını bu sayfanın sonunda bize bildirebilir misiniz? Kolayca başvurabilmek için İngilizce makaleye buradan ulaşabilirsiniz.
Bu makalede, bir Microsoft Excel eklenti programı olan ve en iyi ürün karışımını belirlemek için kullanabileceğiniz bir Microsoft Excel eklenti programı olan çözücü kullanımı açıklanır.
Karlılığı en üst düzeye çıkaran aylık ürün karışımını nasıl belirleyebilirim?
Şirketlerin genellikle aylık olarak üretilecek her ürünün miktarını belirlememesi gerekir. En basit biçimiyle, ürün karması sorunu, karları en üst düzeye çıkarmak için bir ay içinde üretilmesi gereken her ürün miktarının nasıl belirleneceğini kapsar. Ürün karması genellikle aşağıdaki kısıtlamalara bağlı olmalıdır:
-
Ürün karması kullanılabileceğinden daha fazla kaynak kullanamaz.
-
Her ürün için sınırlı bir talep vardır. Fazla üretimin çok fazla üretimi harcandığından (örneğin, Perishable uyuşturucu), bir ay içinde bir daha fazla ürün üretemiyoruz.
Şimdi ürün karması sorununun aşağıdaki örneğini çözelim. Çözüm 27-1 'da gösterilen Prodmix. xlsx dosyasında bu soruna çözüm bulabilirsiniz.
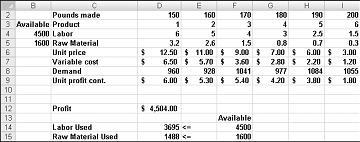
Bu, tesislerinde altı farklı ürün üreten bir ilaç şirketinde iş yaptık. Her ürünün üretimi işçi ve hammadde gerektirir. Þekil 27-1, şekil her bir üründen poundu üretmek için gereken işçiliki gösterir ve satır 5 her bir üründen poundu üretmek için gereken hammadde libre miktarını gösterir. Örneğin, 1 ' in 0 saatlik işçiliği ve 3,2 libre hammadde olmasını gerektirir. Her ilaç Için, libre başına fiyatı satır 6 ' da verilir, libre başına birim maliyeti satır 7 ' de verilir ve kar başına kar katkısı satır 9 ' da verilir. Örneğin, numara libre başına $11,00 için ürün 2 ' nin sattığı, libre başına $5,70 birim maliyeti Her uyuşturucu için ayın talebi 8. Örneğin, 3 ürünü için talep 1041 libre olur. Bu ay, 4500 mesai ve 1600 libre hammadde mevcuttur. Bu şirket aylık karı nasıl en yüksek düzeye çıkarır?
Excel Çözücü hakkında hiçbir şey olduğunu düşünüyorsanız, ürün karışımıyla ilişkili kar ve kaynak kullanımını izlemek için bir çalışma sayfası oluşturarak bu soruna neden olabiliriz. Ardından, daha fazla işçilik veya hammadde kullanmadan ve isteğe bağlı olarak herhangi bir ilaç üretmeksizin kar düzeyini en iyi duruma getirmek için, deneme ve hata 'ı kullanacağız. Çözücü 'yü yalnızca deneme ve hata aşamasında kullanırız. Aslında, çözücü, deneme ve hata aramasını gerçekleştiren en iyi duruma getirme altyapısıdır.
Ürün karması sorununu çözme anahtarı, belirli bir ürün karışımından sonra kaynak kullanımını ve karı verimli şekilde hesaplamanıza olanak sağlar. Bu hesaplamayı yapmak için kullanabileceğiniz önemli bir araç. TOPÇARP işlevi, hücre aralıklarındaki karşılık gelen değerleri çarpar ve bu değerlerin toplamını verir. SUMPRODUCT değerlendirmesinde kullanılan her hücre aralığının aynı boyutlara sahip olması gerekir; bu, tek bir sütun ve tek bir satırla değil, TOPÜRÜNÜ iki satır veya iki sütun ile birlikte kullanamazsınız.
Ürünümüz örneğimizde SUMÇARP işlevini kullanmanın bir örneği olarak, kaynak kullanımımızı hesaplamanıza deneyelim. İşçilik kullanımımız
(Harcırah, harcırah 1) * (ilaç 1 libre üretilmiş) + (uyuşturucu2 libre için kullanılan işgücü) + (ilaç 2 libre üretilmiş) +...(Uyuşturucu 6 libre başına kullanılan işgücü) * (ilaç 6 libre üretilmiş)
İşçi kullanımını D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4olarak daha sıkıcı bir şekilde hesapladık. Aynı şekilde, hammadde kullanımı D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + I2 * I5olarak hesaplanır. Ancak, altı ürün için çalışma sayfasına bu formülleri girmek zaman alır. Örneğin, tesislerinde 50 ürünleri gibi üretilmiş bir şirketle çalışıyorsanız ne kadar süreceğini düşünün. İşçilik ve hammadde kullanımının hesaplanmamesinden çok daha kolay bir yolu, D14 'den D15 ($D $2: $I $2, D4: I4)formülü. Bu formülde D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4 (işçilik kullanımımız olan) Formülü kopyaladığımda, yine de satır 2 ' den ürün karışımını kaydettiğimde, D2: I2 D15 hücresindeki formül, hammadde kullanımını hesaplar.
Benzer şekilde, karımız
(Sayı başına uyuşturucu 1 karı) * (ilaç başına 1 kar) + (ilaç için uyuşturucu 2 karı) * (ilaç 2 libre üretilmiş) +...(Uyuşturucu başına 6 kar) * (ilaç 6 libre üretilmiş)
Kar, D12 hücresine (D9: I9, $D $2: $I $2)kolayca hesaplanır.
Şimdi ürün karması çözücü modelinizin üç bileşenini tanımlayabiliriz.
-
Hedef hücre.Amacınız karı en yükseğe çıkarmaktır (D12 hücresinde hesaplanır).
-
Hücreleri değiştirme.Her bir üründen üretilen libre sayısı (D2: I2 hücre aralığında listelenir)
-
Ları. Aşağıdaki kısıtlamalara sahibiz:
-
Kullanılabileceğinden daha fazla işçilik veya hammadde kullanmayın. Yani, D14: D15 (kullanılan kaynaklar) hücrelerindeki değerler, F14: F15 hücrelerindeki (kullanılabilir kaynaklar) değerlerinden küçük veya eşit olmalıdır.
-
İsteğe bağlı olarak daha fazlasını oluşturmayın. Yani, D2: I2 (libre her bir ilaç için üretilmiş) hücrelerindeki değerler her uyuşturucu (D8 hücrelerinde listelenen I8) talebinin değerinden küçük veya buna eşit olmalıdır.
-
Herhangi bir ilaç için negatif bir miktar üretemiyoruz.
-
Hedef hücreyi, hücre değiştirmeyi ve kısıtlamaları çözücü 'ye nasıl gireceğim. Böylece, tek yapmanız gereken, bir kar-bit düzeni
Başlamak Için veri sekmesini tıklatın ve çözümleme grubunda çözücü 'yü tıklatın.
Not: Bölüm 26 ' da açıklandığı gibi, "Excel çözücü ile en iyi duruma getirmeye bir giriş" çözücü, Microsoft Office düğmesi Yönet listesinde Excel eklentileri 'ni tıklatın, Çözücü eklentisi kutusunu işaretleyin ve Tamam 'ı tıklatın.
Þekil 27-2 gösterildii gibi Çözücü parametreleri iletişim kutusu görüntülenecektir.
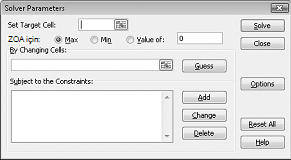
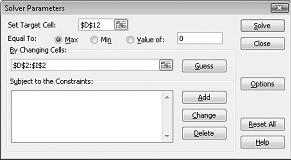
Hedef hücreyi ayarla kutusuna tıklayın ve ardından kar hücremizi (hücre D12) seçin. Hücreleri değiştirerek kutusuna tıklayın ve her ilaç için üretilmiş libre 'i içeren D2: I2 aralığının üzerine gelin. İletişim kutusunda şekil 27-3 görünmelidir.
Artık modele sınırlamalar eklemeye hazırız. Ekle düğmesini tıklatın. Şekil 27-4 gösterilen kısıtlama Ekle iletişim kutusunu görürsünüz.
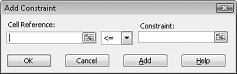
Kaynak kullanım kısıtlamalarını eklemek Için, hücre başvurusu kutusunu tıklatın ve D14: D15 aralığını seçin. Orta listeden < = öğesini seçin. Sınırlama kutusuna tıklayın ve F14: F15 hücre aralığını seçin. Kısıtlama Ekle iletişim kutusu şimdi Şekil 27-5 gibi görünmelidir.
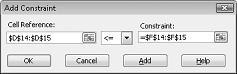
Çözücü 'nün değişen hücreler için farklı değerler denediği durumlarda, yalnızca D14< = F14 (çalışan işçiliki veya buna eşit) ve D15< = F15 (kullanılan hammaddeler kullanılabilir hammadde) dikkate alınır. Talep kısıtlamalarını girmek için Ekle 'yi tıklatın. Şekil 27-6 gösterilen kısıtlama Ekle iletişim kutusunu doldurun.
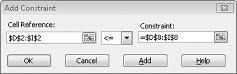
Bu sınırlamaların eklenmesi, çözücü 'nün değişen hücre değerleri için farklı birleşimler yapmaya çalışacağı durumlarda, yalnızca aşağıdaki parametreleri karşılayan birleşimler dikkate alınır:
-
D2< = D8 (Ilaç 1 ' den üretilen tutar, uyuşturucu 1 ' den küçük veya buna eşittir)
-
E2< = E8 (uyuşturucu 2 ' nin üretilen miktarı, uyuşturucu 2 talebinin değerinden azdır veya buna eşittir)
-
F2< = F8 (Ilaç 3 ' ün üretildiği miktar, uyuşturucu 3 talebinin küçüktür veya buna eşittir)
-
G2< = G8 (Ilaç 4 ' ün üretildiği miktar, uyuşturucu 4 talebine eşit veya bundan azdır)
-
H2< = H8 (Ilaç 5 ' in üretildiği miktar, uyuşturucu 5 talebinin altında veya buna eşittir)
-
I2< = I8 (Ilaç 6 ' nın üretildiği miktar, uyuşturucu 6 için talebe eşit veya daha küçüktür)
Kısıtlama Ekle iletişim kutusunda Tamam 'ı tıklatın. Çözücü penceresi Şekil 27-7 gibi görünmelidir.
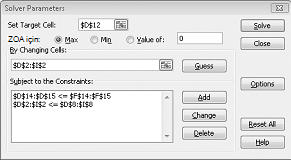
Çözücü Seçenekleri iletişim kutusunda, hücreleri değiştiren kısıtlama seçeneğini aşmamalıdır. Çözücü parametreleri iletişim kutusunda Seçenekler düğmesini tıklatın. Sonraki sayfada, Şekil 27-8 gösterildiği gibi doğrusal modeli varsay kutusunu ve negatif olmayan varsay kutusunu Işaretleyin. Tamam'a tıklayın.
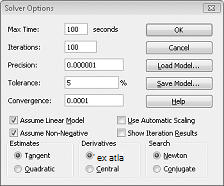
Negatif olmayan varsay kutusunun Işaretlenmesi, çözücü 'nün, değişen her hücrede negatif olmayan bir değer olduğu varsayıldıkları hücre birleşimlerini dikkate almasını sağlar. Ürün karması sorunu, Doğrusal modelolarak bilinen özel bir çözücü sorunu türü olduğundan, doğrusal modeli varsay kutusunu denetdik. Aslında, Çözücü modeli aşağıdaki koşullarda doğrusal olur:
-
Hedef hücre, form şartları (hücre değiştirme) * (Sabit)eklenerek hesaplanır.
-
Her kısıtlama "Doğrusal model gereksinimi" dır. Bu, her kısıtlamanın, form terimlerini (hücre değiştirme) (Sabit) ve toplamları bir sabit ile karşılaştıran şekilde değerlendirilme anlamına gelir.
Bu çözücü sorunu neden doğrusal? Hedef hücrelerimiz (kar) şöyle hesaplanır:
(Sayı başına uyuşturucu 1 karı) * (ilaç başına 1 kar) + (ilaç için uyuşturucu 2 karı) * (ilaç 2 libre üretilmiş) +...(Uyuşturucu başına 6 kar) * (ilaç 6 libre üretilmiş)
Bu hesaplama, hedef hücrenin değerinin, form terimlerini (hücre değiştirme) (Sabit)ekleyerek türeten türetilen deseni izler.
İşçilik sınırlamamız, (Harcırah, uyuşturucu 1) * (ilaç 1 libre üretilmiş) + (uyuşturucu 2 libre/harcırah) + (ilaç 2 libre üretilmiş) + (Işçilikharcırah/uyuşturucu 6) * (ilaç 6 libre üretilmiş) işçilik için kullanılabilir.
Bu nedenle, işçi kısıtlaması, form terimlerini (hücre değiştirme) * (Sabit) ekleyerek ve toplamları sabit ile karşılaştırarak değerlendirilir. Hem işçi kısıtlaması hem de hammadde kısıtlaması Doğrusal model gereksinimini karşılar.
Talep sınırlamalarımız formu alır
(İlaç 1 üretilmiş) _LT_ = (ilaç 1 talep) (ilaç 2 üretilmiş) _LT_ = (ilaç 2 Demand) § (ilaç 6 üretilmiş) _LT_ = (ilaç 6 talep)
Her talep kısıtlaması aynı zamanda Doğrusal model gereksinimini de karşılar, çünkü her biri formun terimlerini birbirine ekleyerek (hücreyi değiştirerek) * (Sabit) ve toplamları sabitlerle karşılaştırır.
Ürün karması modelinin doğrusal bir model olduğunu göstermiştir, neden dikkat ediyoruz?
-
Çözücü modeli Doğrusal ise ve doğrusal modeli varsay ' ı seçmemiz durumunda, çözücü 'Nün en uygun çözümü bulması için çözücü garantilenir. Çözücü modeli Doğrusal değilse, çözücü en iyi çözümü bulabilir veya bulamamış olabilir.
-
Çözücü modeli Doğrusal olduğunda, çözücü, modelin en iyi çözümünü bulmak için çok etkili bir algoritma (simpleks yöntemi) kullanır. Çözücü modeli Doğrusal ise ve Doğrusal model varsay ' ı seçmiyorsa, çözücü çok verimsiz bir algoritma (GRG2 yöntemi) kullanır ve modelin en iyi çözümünü bulmada zorluk çekebilir.
Çözücü Seçenekleri iletişim kutusunda Tamam 'ı tıklattıktan sonra, Şekil 27-7 daha önce gösterilen ana çözücü iletişim kutusuna geri döndürüyoruz. Çöz 'e tıkladığımızda, çözücü, ürün karışım modeliniz için en uygun çözümü (varsa) hesaplar. Bölüm 26 ' da belirtildiği gibi, ürün karışım modeli için en uygun bir çözüm, uygun olan tüm çözümlerin bir kümesini en üst düzeye çıkaran bir dizi değiştirme Yine, uygun bir çözüm, tüm kısıtlamaları yerine getiren bir dizi değişen hücre değerleridir. Şekil 27-9 gösterilen değişen hücre değerleri, tüm üretim düzeyleri negatif olmadığı için, üretim düzeyleri talebi aşmadığından ve kaynak kullanımı kullanılabilir kaynakları aşmadığından uygulanabilir bir çözümdür.
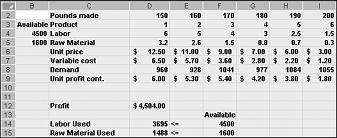
Sonraki sayfada Şekil 27-10 gösterilen değişen hücre değerleri, aşağıdaki nedenlerden dolayı uygun olmayan bir çözümü temsil eder:
-
İsteğe bağlı olarak daha fazla Ilaç 5 üretebiliriz.
-
Kullanılabilir miktardan fazla işgücü kullanırız.
-
Kullanılabilir miktardan daha fazla RAW malzemesi kullanırız.
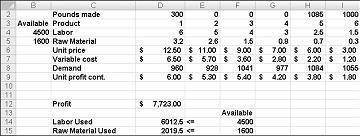
Çöz 'ü tıklattıktan sonra, çözücü, Şekil 27-11 gösterilen en uygun çözümü hızlıca bulur. Çalışma sayfasındaki en iyi çözüm değerlerini korumak için çözücü çözümünü sakla öğesini seçmeniz gerekir.
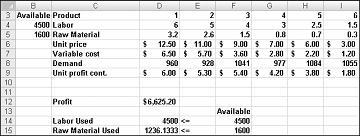
İlaç şirketiniz, $6.625,20 libre,, libre 5 ve diğer uyuşturucu dışında, aylık kârı $6.625,20 'in maksimum karmasına başka yollarla ulaşabildiğimiz konusunda karar vermiyoruz. Tüm sınırlı kaynaklarımız ve taleplerimizle, bu ay $6.627,20 fazlasını yapmanın bir yolu yoktur.
Her ürünün talebinin karşılanması gerektiğini varsayalım . (Prodmix. xlsx dosyasındaki uygulanabilir çözüm yok sayfasına bakın.) Ardından D2: I2< = D8: I8 ile D2: I2> = D8: I8olan talep kısıtlamalarını değiştirmemiz gerekir. Bunu yapmak Için, çözücü 'yü açın, D2: I2< = D8: I8 kısıtlamasını seçin ve sonra da Değiştir 'e tıklayın. Şekil 27-12 gösterilen kısıtlama Değiştir iletişim kutusu görüntülenir.
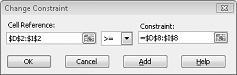
_GT_ = öğesini ve sonra Tamam 'ı tıklatın. Şimdi, çözücü 'nün yalnızca tüm talepleri karşılayan hücre değerlerini değiştirmesini düşünüyoruz. Çöz 'ü tıklattığınızda, "çözücü uygun bir çözüm bulamadı" iletisini görürsünüz. Bu ileti modelinizde bir hata yaptık, ancak sınırlı kaynaklarımız yerine tüm ürünlerin talebini karşılayamıyoruz. Çözücü, her bir ürünün talebini karşılamak istiyordığımızdaki, daha fazla işçilik, daha fazla hammadde veya daha fazlasını eklemememiz gerektiğini mi bildiriyor?
Her bir ürün için sınırsız talebe izin vermemiz durumunda ne olduğunu ve her bir ilaç için negatif miktarların üretilmesi gerektiğini görelim. (Bu çözücü sorununu, değerleri ayarlama Işlemi, Prodmix. xlsx dosyasındaki değerleri yakınlaşmıyor .) Bu durumla ilgili en iyi çözümü bulmak Için, çözücü 'yü açın, Seçenekler düğmesine tıklayın ve negatif olmayan varsay kutusunun işaretini kaldırın. Çözücü parametreleri iletişim kutusunda, D2: I2< = D8: I8 talep kısıtlamasını seçin ve sonra da kısıtlamayı kaldırmak için Sil 'e tıklayın. Çöz 'ü tıklattığınızda, çözücü, "hücre değerlerini ayarla dönüşmiyor" iletisini verir. Bu iletide, hedef hücre ekranı kaplayamıyorsa (örneğimizde olduğu gibi), çok büyük hedef hücre değerleriyle ilgili uygun çözümler vardır. (Hedef hücre simge durumuna küçültülmüşse, "hücre değerlerini ayarla yakınlaşmaz" iletisi, çok küçük hedef hücre değerleriyle uygulanabilir çözümler olduğu anlamına gelir. Bu durumumuzda, bir uyuşturucu 'in negatif üretimine izin vererek, rasgele büyük miktarlarda başka uyuşturucu üretmek için kullanılabilecek kaynaklar Sınırsız taleplerimiz sayesinde, sınırsız kar yapabiliriz. Gerçek bir durumda sonsuz miktarda para yapamıyoruz. Kısaca, "değerleri ayarla yakınlaşmıyor" ifadesini görürseniz, modelinizde bir hata vardır.
-
İlaç şirketimizin en çok 500 saat işçiliği, geçerli işçilik maliyetinden saatte bir saat. Karı en iyi duruma getirme
-
Yonga üretim tesiste, dört teknisyen (A, B, C ve D) üç ürün üretecektir (Ürünler 1, 2 ve 3). Bu ay, yonga üreticisi 80 ürün 1, 50 birimleri ürün 2 ve en çok 50 ürün 3 birimi. Teknisyen A yalnızca 1 ve 3 ürünlerini yapabilir. Teknisyen B yalnızca 1 ve 2 ürünlerini oluşturabilir. Teknisyen C yalnızca ürün 3 yapabilir. Teknisyen D yalnızca ürün 2 yapabilir. Üretilen her birim Için, ürünler şu karı katkıda vardır: ürün 1, $6; Ürün 2, $7; ve ürün 3, $10. Her teknisyenin bir ürünü üretmesinde gerekli süre (saat olarak) aşağıdaki gibidir:
Ürün
Teknisyen A
Teknisyen B
Teknisyen C
Teknisyen D
1
2
2,5
Yapılamıyor
Yapılamıyor
2
Yapılamıyor
3
Yapılamıyor
3,5
3
3
Yapılamıyor
4
Yapılamıyor
-
Her teknisyen ayda 120 saate kadar çalışabilir. Yonga üreticiniz aylık karı nasıl en yüksek düzeye çıkarır? Kesirli birimlerin üretilmekte olduğunu varsayalım.
-
Bilgisayar üretim tesisi fareler, klavyeler ve video oyun oyun çubukları üretir. Birim başına kar, birim başına işçilik kullanımı, aylık talep ve birim başına makine başına kullanım, aşağıdaki tabloda verilmiştir:
Eleri
Klavyede
Çubuğu
Kar/birim
$8
$11
$9
Işçi kullanımı/birimi
.2 saat
.3 saat
.24 saat
Makine süresi/birimi
.04 Saat
.055 saat
.04 Saat
Aylık talep
15.000
27.000
11.000
-
Her ay, toplam 13.000 işgücü saat ve 3000 saat kullanılabilir. Üreticiye ait aylık kar katkısını nasıl en yüksek düzeye çıkartabilir?
-
Uyuşturucu örneğimizi, her bir uyuşturucu için en az 200 biriminin karşılanması gerektiğini varsayarak çözün.
-
Jason, karo brateni, necklaces ve kazanma halkaları yapar. Ayda maksimum 160 saat çalışmak istiyor. 800 elmasları için. Her ürünü oluşturmak için gereken kar, işçi süresi ve karo Her bir ürün için talep yoksa kar
Ürün
Birim karı
Birim başına Işçilik saatleri
Birim başına karo
Brezilya
300 TL
.35
1.2
Necklace
200 TL
.15
.75
Muydun
100 TL
0,05
0,5










