Tek terimli binom dağılımı olasılığını verir. BİNOMDAĞ işlevini, sabit test veya deneme sayısı olan problemlerde, denemelerin sonucu yalnızca başarılı veya başarısızsa, denemeler bağımsızsa ve başarı olasılığı deney boyunca sabitse kullanın. Örneğin, BİNOMDAĞ, doğacak ilk üç çocuktan ikisinin erkek olma olasılığını hesaplayabilir.
Önemli: Bu işlevin yerini, daha iyi bir doğruluk sağlayabilecek ve adları kullanımlarını daha iyi yansıtan bir veya daha fazla yeni işlev almıştır. Geriye dönük uyumluluk açısından bu işlev halen kullanılabilir olmakla birlikte, Excel'in gelecek sürümlerinde bulunmayabileceğinden bundan sonra yeni işlevleri kullanmaya başlamayı düşünmelisiniz.
Yeni işlev hakkında daha fazla bilgi için bkz. BİNOM.DAĞ işlevi.
Söz Dizimi
BİNOMDAĞ(başarı_sayısı,denemeler,başarı_olasılığı,kmülatif)
BİNOMDAĞ işlevinin söz diziminde aşağıdaki bağımsız değişkenler vardır:
-
Başarı_sayısı Gerekli. Denemelerdeki başarı sayısıdır.
-
Deneme Gerekli. Bağımsız deneme sayısıdır.
-
Olasılık_b Gerekli. Her denemedeki başarı olasılığıdır.
-
Kümülatif Gerekli. İşlevin biçimini belirleyen mantıksal değerdir. Kümülatif DOĞRU ise, BİNOMDAĞ, en çok başarı_sayısı başarı olasılığı olan kümülatif dağılım işlevini verir, YANLIŞ ise, başarı_sayısı başarı olasılığı olan olasılık yığın işlevini verir.
Notlar
-
Sayı_b ve deneme, tamsayı değerlerine yuvarlanır.
-
Sayı_b, deneme veya olasılık_b sayısal değilse, BİNOMDAĞ işlevi, #VALUE! hata değerini verir.
-
Sayı_b < 0 veya sayı_b > deneme ise, BİNOMDAĞ işlevi, #SAYI! hata değerini verir.
-
Olasılık_b < 0 veya olasılık_b > 1 ise, BİNOMDAĞ işlevi, #SAYI! hata değerini verir.
-
x = sayı_b, n = deneme ve p = olasılık_b ise, kütle işlevinin binom olasılığı:
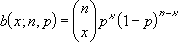
burada:

KOMBİNASYON(n;x)'dir.
-
x = sayı_b, n = deneme ve p = olasılık_b ise, kümülatif binom dağılımı:
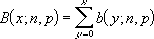
Örnek
Aşağıdaki tabloda yer alan örnek verileri kopyalayın ve yeni bir Excel çalışma sayfasının A1 hücresine yapıştırın. Formüllerin sonuçları göstermesi için, bunları seçip F2 tuşuna basın ve sonra Enter tuşuna basın. Gerekirse, tüm verileri görmek için sütun genişliğini ayarlayabilirsiniz.
|
Veri |
Açıklama |
|
|
6 |
Denemelerdeki başarı sayısı |
|
|
10 |
Bağımsız denemelerin sayısı |
|
|
0,5 |
Her denemede başarı olasılığı |
|
|
Formül |
Açıklama |
Sonuç |
|
=BİNOMDAĞ(A2;A3;A4;YANLIŞ) |
10 denemenin tam 6'sının başarılı olma olasılığı. |
0,2050781 |










