บริษัทสามารถใช้ Solver เพื่อกําหนดโครงการที่บริษัทควรดําเนินการได้อย่างไร
ในแต่ละปี บริษัท เช่น Eli Lilly ต้องพิจารณาว่ายาใดที่จะพัฒนา บริษัทเช่น Microsoft ซึ่งโปรแกรมซอฟต์แวร์ใดที่จะพัฒนา บริษัท เช่น Proctor & Gamble ซึ่งผลิตภัณฑ์สําหรับผู้บริโภคใหม่ที่จะพัฒนา ฟีเจอร์ Solver ใน Excel สามารถช่วยให้บริษัททําการตัดสินใจเหล่านี้ได้
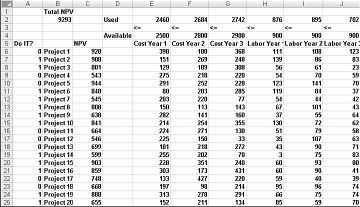
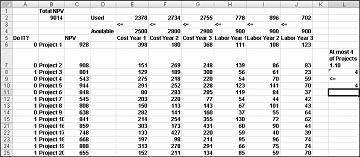
บริษัทส่วนใหญ่ต้องการดําเนินการโครงการที่มีส่วนร่วมในมูลค่าปัจจุบันสุทธิที่ยิ่งใหญ่ที่สุด (NPV) ขึ้นอยู่กับทรัพยากรที่ จํากัด (โดยปกติจะเป็นเงินทุนและแรงงาน) สมมติว่า บริษัท พัฒนาซอฟต์แวร์กําลังพยายามระบุว่าควรดําเนินการโครงการซอฟต์แวร์ใด 20 โครงการ NPV (ในหลายล้านดอลลาร์) ที่ได้รับการสนับสนุนโดยแต่ละโครงการรวมถึงเงินทุน (เป็นล้านดอลลาร์) และจํานวนโปรแกรมเมอร์ที่จําเป็นในช่วงสามปีถัดไปจะได้รับในเวิร์กชีต รูปแบบพื้นฐาน ในไฟล์ Capbudget.xlsx ซึ่งจะแสดงในรูปภาพ 30-1 ในหน้าถัดไป ตัวอย่างเช่น Project 2 ให้ผลตอบแทน $908 ล้าน มันต้องมี $151 ล้านในช่วงปี 1, $269 ล้านในช่วงปี 2, และ $248 ล้านในช่วงปีที่ 3. Project 2 ต้องการโปรแกรมเมอร์ 139 โปรแกรมเมอร์ในช่วงปีที่ 1, 86 ระหว่างโปรแกรมเมอร์ปีที่ 2 และ 83 ระหว่างปีที่ 3 เซลล์ E4:G4 แสดงตัวพิมพ์ใหญ่ (เป็นล้านดอลลาร์) ที่พร้อมใช้งานระหว่างแต่ละสามปี และเซลล์ H4:J4 แสดงจํานวนโปรแกรมเมอร์ที่พร้อมใช้งาน ตัวอย่างเช่น ในช่วงปีที่ 1 มีเงินทุนสูงสุด $2.5 พันล้านเหรียญและโปรแกรมเมอร์ 900 โปรแกรมพร้อมใช้งาน
บริษัทต้องตัดสินใจว่าควรดําเนินแต่ละโครงการหรือไม่ สมมติว่าเราไม่สามารถดําเนินการกับโครงการซอฟต์แวร์ได้ ถ้าเราจัดสรรทรัพยากรที่จําเป็น 0.5 รายการ ตัวอย่างเช่น เราจะมีโปรแกรมที่ไม่ทํางานซึ่งจะนํามาซึ่งรายได้ $0!
เคล็ดลับในสถานการณ์การสร้างแบบจําลองที่คุณทําหรือไม่ทําอะไรบางอย่างคือการใช้เซลล์ที่เปลี่ยนไบนารี เซลล์ที่เปลี่ยนไบนารีจะเท่ากับ 0 หรือ 1 เสมอ เมื่อเซลล์ที่มีการเปลี่ยนไบนารีที่สอดคล้องกับโครงการเท่ากับ 1 เราจะทําโครงการ ถ้าเซลล์ที่มีการเปลี่ยนไบนารีที่สอดคล้องกับโครงการเท่ากับ 0 เราจะไม่ทําโครงการ คุณตั้งค่า Solver ให้ใช้ช่วงของเซลล์ที่เปลี่ยนแปลงไบนารีโดยการเพิ่มข้อจํากัด เลือกเซลล์ที่เปลี่ยนแปลงที่คุณต้องการใช้ แล้วเลือก Bin จากรายการในกล่องโต้ตอบ เพิ่มข้อจํากัด
ด้วยพื้นหลังนี้เราพร้อมที่จะแก้ไขปัญหาการเลือกโครงการซอฟต์แวร์ เช่นเดียวกับรูปแบบ Solver เราเริ่มต้นด้วยการระบุเซลล์เป้าหมาย เซลล์ที่เปลี่ยนแปลง และข้อจํากัดของเรา
-
เซลล์เป้าหมาย เราขยาย NPV ที่สร้างโดยโครงการที่เลือก
-
การเปลี่ยนเซลล์ เราค้นหาเซลล์ที่เปลี่ยนไบนารี 0 หรือ 1 สําหรับแต่ละโครงการ ฉันได้ระบุตําแหน่งเซลล์เหล่านี้ในช่วง A6:A25 (และมีชื่อ ว่าจุดช่วง) ตัวอย่างเช่น 1 ในเซลล์ A6 ระบุว่าเราดําเนินการ Project 1 0 ในเซลล์ C6 ระบุว่าเราไม่ทํา Project 1
-
ข้อจํากัด เราต้องตรวจสอบให้แน่ใจว่าในแต่ละปี t (t=1, 2, 3) ทุน Year t ที่ใช้น้อยกว่าหรือเท่ากับทุน Year t และค่าแรง Year t ที่ใช้น้อยกว่าหรือเท่ากับค่าแรง Year t
อย่างที่คุณเห็นเวิร์กชีตของเราต้องคํานวณสําหรับการเลือกโครงการ NPV ตัวพิมพ์ใหญ่ที่ใช้เป็นประจําทุกปีและโปรแกรมเมอร์ที่ใช้ในแต่ละปี ในเซลล์ B2 ฉันใช้สูตร SUMPRODUCT(doit,NPV) เพื่อคํานวณ NPV ทั้งหมดที่สร้างขึ้นโดยโครงการที่เลือก (ชื่อช่วง NPV หมายถึงช่วง C6:C25) สําหรับทุกโครงการที่มี 1 ในคอลัมน์ A สูตรนี้จะเลือก NPV ของโครงการ และสําหรับทุกโครงการที่มี 0 ในคอลัมน์ A สูตรนี้จะไม่เลือก NPV ของโครงการ ดังนั้น เราจึงสามารถคํานวณ NPV ของโครงการทั้งหมดได้ และเซลล์เป้าหมายของเราเป็นแบบเชิงเส้น เนื่องจากถูกคํานวณโดยสรุปเงื่อนไขที่ตามหลังฟอร์ม (เซลล์ที่เปลี่ยนแปลง)*(ค่าคงที่) ในลักษณะเดียวกันฉันคํานวณเงินทุนที่ใช้ในแต่ละปีและแรงงานที่ใช้ในแต่ละปีโดยการคัดลอกจาก E2 ถึง F2:J2 สูตร SUMPRODUCT(doit,E6:E25)
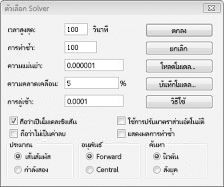
ตอนนี้ฉันใส่ข้อมูลในกล่องโต้ตอบ Solver Parameters ตามที่แสดงในรูป 30-2
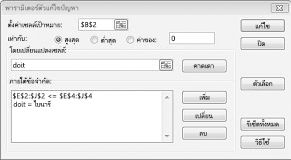
เป้าหมายของเราคือการเพิ่ม NPV ของโครงการที่เลือก (เซลล์ B2) เซลล์ที่เปลี่ยนแปลงของเรา (ช่วงที่ชื่อ doit) คือเซลล์ที่เปลี่ยนไบนารีสําหรับแต่ละโครงการ ข้อจํากัด E2:J2<=E4:J4 ทําให้แน่ใจว่าในแต่ละปีทุนและแรงงานที่ใช้น้อยกว่าหรือเท่ากับทุนและแรงงานที่มีอยู่ เมื่อต้องการเพิ่มข้อจํากัดที่ทําให้เซลล์ไบนารีเปลี่ยนแปลง ฉันคลิก เพิ่ม ในกล่องโต้ตอบ Solver Parameters แล้วเลือก Bin จากรายการที่อยู่ตรงกลางของกล่องโต้ตอบ กล่องโต้ตอบ เพิ่มข้อจํากัด ควรปรากฏตามที่แสดงใน รูปที่ 30-3
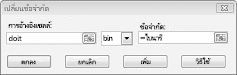
รูปแบบของเราเป็นแบบเชิงเส้นเนื่องจากเซลล์เป้าหมายจะถูกคํานวณเป็นผลรวมของคําที่มีฟอร์ม (เซลล์ที่เปลี่ยน)*(ค่าคงที่) และเนื่องจากข้อจํากัดการใช้ทรัพยากรจะถูกคํานวณโดยการเปรียบเทียบผลรวมของ (เซลล์ที่เปลี่ยน)*(ค่าคงที่) กับค่าคงที่
เมื่อใส่กล่องโต้ตอบ Solver Parameters ให้คลิก Solve และเราได้แสดงผลลัพธ์ก่อนหน้านี้ในรูป 30-1 บริษัทสามารถรับ NPV สูงสุด $9,293 ล้าน ($9.293 พันล้าน) โดยการเลือกโครงการ 2, 3, 6–10, 14–16, 19 และ 20
ในบางครั้ง แบบจําลองการเลือกโครงการจะมีข้อจํากัดอื่นๆ ตัวอย่างเช่นสมมติว่าถ้าเราเลือก Project 3 เราต้องเลือก Project 4 ด้วย เนื่องจากโซลูชันที่เหมาะสมในปัจจุบันของเราเลือก Project 3 แต่ไม่ใช่ Project 4 เราจึงทราบว่าโซลูชันปัจจุบันของเราไม่สามารถรักษาให้เหมาะสมได้ เมื่อต้องการแก้ไขปัญหานี้ เพียงเพิ่มข้อจํากัดที่เซลล์ที่เปลี่ยนไบนารีสําหรับ Project 3 น้อยกว่าหรือเท่ากับเซลล์ที่เปลี่ยนไบนารีสําหรับ Project 4
คุณสามารถค้นหาตัวอย่างนี้บนเวิร์กชีต ถ้า 3 แล้ว 4 ในไฟล์ Capbudget.xlsx ซึ่งแสดงในรูป 30-4 เซลล์ L9 หมายถึงค่าไบนารีที่เกี่ยวข้องกับ Project 3 และเซลล์ L12 ไปยังค่าไบนารีที่เกี่ยวข้องกับ Project 4 ด้วยการเพิ่มข้อจํากัด L9<=L12 ถ้าเราเลือก Project 3, L9 เท่ากับ 1 และข้อจํากัดของเราบังคับ L12 (ไบนารี Project 4) ให้เท่ากับ 1 ข้อจํากัดของเราต้องปล่อยให้ค่าไบนารีในเซลล์ที่เปลี่ยนแปลงของ Project 4 ไม่จํากัดถ้าเราไม่ได้เลือก Project 3 ถ้าเราไม่เลือก Project 3, L9 เท่ากับ 0 และข้อจํากัดของเราอนุญาตให้ไบนารี Project 4 เท่ากับ 0 หรือ 1 ซึ่งเป็นสิ่งที่เราต้องการ โซลูชันที่เหมาะสมแบบใหม่จะแสดงในรูป 30-4
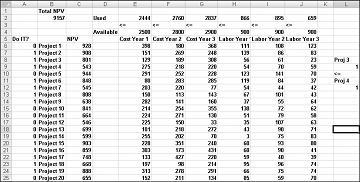
โซลูชั่นที่ดีที่สุดใหม่จะถูกคํานวณหากเลือก Project 3 หมายความว่าเราต้องเลือก Project 4 ด้วย ตอนนี้สมมติว่าเราสามารถทําโครงการได้เพียงสี่โครงการจากโครงการ 1 ถึง 10 (ดู ที่เวิร์กชีต P1-P10 มากที่สุด 4 รายการ ซึ่งแสดงในรูป 30-5) ในเซลล์ L8 เราคํานวณผลรวมของค่าไบนารีที่เกี่ยวข้องกับ Projects 1 ถึง 10 ด้วยสูตร SUM(A6:A15) จากนั้นเราจะเพิ่มข้อจํากัด L8<=L10 ซึ่งทําให้แน่ใจได้ว่ามีการเลือกโครงการ 4 ใน 10 โครงการแรกเป็นส่วนใหญ่ โซลูชันที่เหมาะสมแบบใหม่จะแสดงในรูป 30-5 NPV ลดลงสู่ 9.014 พันล้านดอลลาร์
รูปแบบ Solver เชิงเส้นซึ่งเซลล์ที่เปลี่ยนแปลงบางเซลล์หรือทั้งหมดจะต้องเป็นเลขฐานสองหรือจํานวนเต็มมักจะแก้ไขได้ยากกว่าโมเดลเชิงเส้นซึ่งเซลล์ที่เปลี่ยนแปลงทั้งหมดได้รับอนุญาตให้เป็นเศษส่วน ด้วยเหตุนี้ เรามักจะพอใจกับโซลูชันที่ใกล้เคียงที่สุดกับปัญหาการเขียนโปรแกรมไบนารีหรือจํานวนเต็ม ถ้าตัวแบบ Solver ของคุณทํางานเป็นเวลานาน คุณอาจต้องการพิจารณาปรับการตั้งค่า ค่าเผื่อ ในกล่องโต้ตอบ Solver Options (ดูรูป 30-6) ตัวอย่างเช่น การตั้งค่าค่าความคลาดเคลื่อน 0.5% หมายความว่า Solver จะหยุดในครั้งแรกที่พบโซลูชันที่เป็นไปได้ ซึ่งอยู่ภายใน 0.5 เปอร์เซ็นต์ของค่าเซลล์เป้าหมายที่เหมาะสมตามทฤษฎี (ค่าเซลล์เป้าหมายที่เหมาะสมตามทฤษฎีคือค่าเป้าหมายที่เหมาะสมที่สุดที่พบเมื่อละเว้นข้อจํากัดแบบไบนารีและจํานวนเต็ม) บ่อยครั้งที่เรากําลังเผชิญกับทางเลือกระหว่างการค้นหาคําตอบภายใน 10 เปอร์เซ็นต์ของประสิทธิภาพสูงสุดใน 10 นาทีหรือค้นหาโซลูชันที่เหมาะสมภายในสองสัปดาห์ที่ผ่านมา! ค่าความคลาดเคลื่อนเริ่มต้นคือ 0.05% ซึ่งหมายความว่า Solver จะหยุดเมื่อพบค่าเซลล์เป้าหมายภายใน 0.05 เปอร์เซ็นต์ของค่าเซลล์เป้าหมายที่เหมาะสมตามทฤษฎี
-
บริษัทมีโครงการ 9 โครงการอยู่ระหว่างการพิจารณา NPV ที่เพิ่มโดยแต่ละโครงการและเงินทุนที่กําหนดโดยแต่ละโครงการในช่วงสองปีถัดไปจะแสดงในตารางต่อไปนี้ (ตัวเลขทั้งหมดเป็นล้าน) ตัวอย่างเช่น Project 1 จะเพิ่มเงิน 14 ล้านดอลลาร์ใน NPV และต้องใช้ค่าใช้จ่าย $12 ล้านในช่วงปีที่ 1 และ 3 ล้านดอลลาร์ในช่วงปีที่ 2 ในช่วงปีที่ 1 มีเงินทุน 50 ล้านดอลลาร์สําหรับโครงการและ 20 ล้านดอลลาร์สามารถใช้ได้ในช่วงปีที่ 2
|
NPV |
รายจ่ายปีที่ 1 |
รายจ่ายปีที่ 2 |
|
|---|---|---|---|
|
Project 1 |
14 |
1.2 |
3 |
|
Project 2 |
17 |
54 |
7 |
|
Project 3 |
17 |
6 |
6 |
|
Project 4 |
15 |
6 |
2 |
|
Project 5 |
40 |
30 |
35 |
|
Project 6 |
1.2 |
6 |
6 |
|
Project 7 |
14 |
48 |
4 |
|
Project 8 |
10 |
36 |
3 |
|
Project 9 |
1.2 |
18 |
3 |
-
หากเราไม่สามารถดําเนินโครงการบางส่วนได้ แต่ต้องดําเนินโครงการใดโครงการหนึ่งทั้งหมดหรือไม่มีเลย เราจะเพิ่ม NPV ให้ถึงขนาดสูงสุดได้อย่างไร
-
สมมติว่าถ้าโครงการ 4 ดําเนินการอยู่ โครงการ 5 จะต้องดําเนินการ เราจะขยาย NPV ให้ถึงขีดสุดได้อย่างไร
-
บริษัทสํานักพิมพ์พยายามกําหนดหนังสือ 36 เล่มที่ควรเผยแพร่ในปีนี้ ไฟล์ Pressdata.xlsx ให้ข้อมูลเกี่ยวกับหนังสือแต่ละเล่มดังต่อไปนี้:
-
ต้นทุนรายได้และการพัฒนาที่คาดการณ์ไว้ (หน่วยหลายพันดอลลาร์)
-
หน้าในแต่ละหนังสือ
-
หนังสือเล่มนี้มุ่งไปที่ผู้ชมของนักพัฒนาซอฟต์แวร์หรือไม่ (ระบุโดย 1 ในคอลัมน์
บริษัทผู้เผยแพร่สามารถเผยแพร่หนังสือที่มีจํานวนหน้าสูงสุดถึง 8500 หน้าในปีนี้ และต้องเผยแพร่หนังสืออย่างน้อยสี่เล่มที่มุ่งมุ่งสู่นักพัฒนาซอฟต์แวร์ บริษัทสามารถเพิ่มผลกําไรสูงสุดได้อย่างไร
-
บทความนี้ได้รับการดัดแปลงจาก Microsoft Office Excel 2007 Data Analysis and Business Modeling โดย Wayne L. Winston
หนังสือสไตล์ห้องเรียนนี้ได้รับการพัฒนาจากชุดงานนําเสนอโดย Wayne Winston นักสถิติที่รู้จักกันดีและศาสตราจารย์ทางธุรกิจที่เชี่ยวชาญในการใช้งานที่สร้างสรรค์และเป็นประโยชน์ของ Excel










