Returnerar konfidensintervallet för en populations medelvärde genom att använda en normalfördelning.
Beskrivning
Konfidensintervallet är ett intervall med värden. Ditt sampelmedelvärde, x, ligger i mitten av intervallet och intervallet är x ± KONFIDENS.NORM. Om till exempel x är sampelmedelvärdet av leveranstiden för produkter som beställts via post så är x ± KONFIDENS.NORM ett intervall med populationsmedelvärden. För varje populationsmedelvärde, μ0, i det här intervallet, är sannolikheten för att uppnå ett sampelmedelvärde längre från μ0 än x större än alfa och för varje populationsmedelvärde, μ0, utanför det här intervallet, är sannolikheten för att uppnå ett sampelmedelvärde längre från μ0 än x mindre än alfa. Med andra ord, antag att vi använder x, standardavvikelse och storlek för att konstruera ett tvåsidigt test på signifikansnivån alfa för hypotesen att populationsmedelvärdet är μ0. Den hypotesen avvisas inte om μ0 ligger i konfidensintervallet, men avvisas om μ0 inte ligger i konfidensintervallet. Konfidensintervallet tillåter inte slutsatsen att sannolikheten att vårt nästa paket tar en leveranstid som ligger i konfidensintervallet är 1 – alfa.
Syntax
KONFIDENS.NORM(alfa;standardavvikelse;storlek)
Syntaxen för funktionen KONFIDENS.NORM har följande argument:
-
Alfa Obligatoriskt. Den signifikansnivå som används för att beräkna konfidensnivån. Konfidensnivån är 100*(1 - alfa)%, eller med andra ord, ett alfa på 0,05 anger en konfidensnivå på 95 procent.
-
Standardavvikelse Obligatoriskt. Populationens standardavvikelse för dataområdet och den förväntas vara känd.
-
Storlek Obligatoriskt. Sampelstorleken.
Kommentarer
-
Om något argument är icke-numeriskt, KONFIDENS. NORM returnerar #VALUE! felvärdet #REFERENS!.
-
Om alfa ≤ 0 eller alfa ≥ 1, KONFIDENS. NORM returnerar #NUM! felvärdet #REFERENS!.
-
Om standard_dev ≤ 0, KONFIDENS. NORM returnerar #NUM! felvärdet #OGILTIGT!.
-
Om storlek inte är ett heltal, avkortas det.
-
Om storlek < 1, KONFIDENS. NORM returnerar #NUM! felvärdet #REFERENS!.
-
Om vi utgår från att alfa är lika med 0,05, måste vi beräkna området under standardnormalkurvan som är lika med (1 - alfa), eller 95 procent. Detta värde är ± 1.96. Konfidensintervallet är därför:
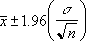
Exempel
Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du justera kolumnbredderna så att alla data visas.
|
Data |
Beskrivning |
|
|
0,05 |
Signifikansnivå |
|
|
2,5 |
Standardavvikelsen för populationen |
|
|
50 |
Sampelstorlek |
|
|
Formel |
Beskrivning |
Resultat |
|
=KONFIDENS.NORM(A2;A3;A4) |
Konfidensintervallet för en populations medelvärde. Konfidensintervallet för det underliggande populationsmedelvärdet för restiden till arbetet är 30 ± 0,692952 minuter, eller 29,3 till 30,7 minuter. |
0,692952 |










