Använda Problemlösaren för kapitalbudgetering

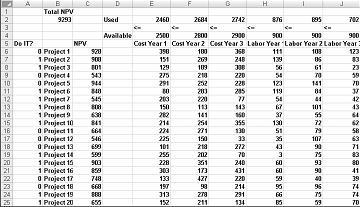
De flesta företag vill genomföra projekt som bidrar med det största nettonuvärdet (NETNUVÄRDE), med begränsade resurser (vanligtvis kapital och arbete). Anta att ett mjukvaruutvecklingsföretag försöker avgöra vilket av 20 programvaruprojekt det ska genomföra. Netnuvärde (i miljontals dollar) som varje projekt bidrar med samt kapitalet (i miljontals dollar) och antalet programmerare som behövs under vart och ett av de kommande tre åren anges i kalkylbladet Grundmodell i filen Capbudget.xlsx, som visas i bild 30-1 på nästa sida. Till exempel ger Project 2 908 miljoner dollar. Det kräver 151 miljoner dollar under år 1, 269 miljoner dollar under år 2 och 248 miljoner dollar under år 3. Projekt 2 kräver 139 programmerare under år 1, 86 programmerare under år 2 och 83 programmerare under år 3. Cellerna E4:G4 visar det kapital (i miljontals dollar) som är tillgängligt under vart och ett av de tre åren, och cellerna H4:J4 anger hur många programmerare som är tillgängliga. Under år 1 finns till exempel upp till 2,5 miljarder dollar i kapital och 900 programmerare tillgängliga.

Företaget måste besluta om det ska genomföra varje projekt. Anta att vi inte kan genomföra en bråkdel av ett programvaruprojekt. om vi allokerar 0,5 av de nödvändiga resurserna, till exempel skulle vi ha ett icke-arbetande program som skulle ge oss $ 0 intäkter!

Tricket i modelleringssituationer där du antingen gör eller inte gör något är att använda binära justerbara celler. En binär justerbar cell är alltid lika med 0 eller 1. När en binär justerbar cell som motsvarar ett projekt är lika med 1 gör vi projektet. Om en binär justerbar cell som motsvarar ett projekt är lika med 0 gör vi inte projektet. Du konfigurerar Problemlösaren till att använda ett område med binära justerbara celler genom att lägga till ett villkor. Markera de justerbara celler som du vill använda och välj sedan Bin i listan i dialogrutan Lägg till villkor.

Med den här bakgrunden är vi redo att lösa problemet med val av programvaruprojekt. Som alltid med en Problemlösaren-modell börjar vi med att identifiera vår målcell, de justerbara cellerna och begränsningarna.

• Målcell. Vi maximerar NETNUVÄRDE som genereras av utvalda projekt.

• Ändra celler. Vi letar efter en binär justerbar cell med 0 eller 1 för varje projekt. Jag har hittat de här cellerna i området A6:A25 (och namngett området doit). Exempel: 1 i cell A6 anger att vi genomför Project 1. a 0 i cell C6 anger att vi inte genomför Project 1.

• Begränsningar. För varje år t (t=1, 2, 3) måste vi se till att det använda kapitalet år t är mindre än eller lika med tillgängligt år t-kapital och Det år t-arbete som används är mindre än eller lika med tillgängligt år t-arbete .

Som du kan se måste vårt kalkylblad beräknas för val av projekt NETNUVÄRDE, det kapital som används årligen och de programmerare som används varje år. I cell B2 använder jag formeln PRODUKTSUMMA(doit;NETNUVÄRDE) för att beräkna det totala NETNUVÄRDE som genererats av valda projekt. (Områdesnamnet NETNUVÄRDE refererar till området C6:C25.) För varje projekt med 1 i kolumn A hämtas projektets NETNUVÄRDE i den här formeln, och för varje projekt med 0 i kolumn A hämtas inte projektets NETNUVÄRDE i den här formeln. Därför kan vi beräkna NETNUVÄRDE för alla projekt och vår målcell är linjär eftersom den beräknas genom att summera termer som följer formuläret (ändra cell)*(konstant). På liknande sätt beräknar jag kapitalet som används varje år och det arbete som används varje år genom att kopiera från E2 till F2:J2 formeln PRODUKTSUMMA(doit,E6:E25).

Jag fyller nu i dialogrutan Parametrar för Problemlösaren enligt bild 30-2.

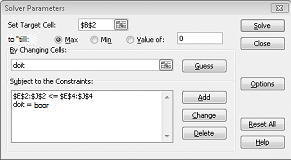
Vårt mål är att maximera NETNUVÄRDE för valda projekt (cell B2). Våra justerbara celler (området doit) är de binära justerbara cellerna för varje projekt. Villkoret E2:J2<=E4:J4 säkerställer att det kapital och arbete som används under varje år är mindre än eller lika med det kapital och arbete som är tillgängligt. Om du vill lägga till villkoret som gör justerbara celler binära klickar jag på Lägg till i dialogrutan Parametrar för Problemlösaren och väljer sedan Bin i listan i mitten av dialogrutan. Dialogrutan Lägg till villkor ska visas enligt bild 30-3.

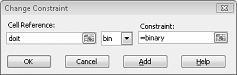
Vår modell är linjär eftersom målcellen beräknas som summan av termer som har formuläret (ändrar cell)*(konstant) och eftersom resursanvändningsbegränsningarna beräknas genom att summan av (justerbara celler)*(konstanter) jämförs med en konstant.

Med dialogrutan Parametrar för Problemlösaren ifylld klickar du på Lös så visas resultaten tidigare i bild 30-1. Företaget kan erhålla maximalt 9 293 miljoner USD (9,293 miljarder USD) genom att välja Projekt 2, 3, 6–10, 14–16, 19 och 20.

Ibland har projekturvalsmodeller andra villkor. Anta till exempel att om vi väljer Project 3 måste vi också välja Project 4. Eftersom vår nuvarande optimala lösning väljer Project 3 men inte Project 4 vet vi att vår nuvarande lösning inte kan förbli optimal. Lös problemet genom att helt enkelt lägga till villkoret att den binära justerbara cellen för Project 3 är mindre än eller lika med den binära justerbara cellen för Project 4.

Det här exemplet finns i kalkylbladet Om 3 och sedan 4 i filen Capbudget.xlsx, som visas i Bild 30-4. Cell L9 refererar till det binära värdet för Project 3 och cell L12 till det binära värdet som är relaterat till Project 4. Genom att lägga till villkoret L9<=L12, om vi väljer Project 3, är L9 lika med 1 och vårt villkor tvingar L12 (binärt Project 4) att vara lika med 1. Villkoret måste också lämna det binära värdet i den justerbara cellen i Project 4 obegränsat om vi inte väljer Project 3. Om vi inte väljer Project 3 är L9 lika med 0 och med vårt villkor kan det binära Project 4 vara lika med 0 eller 1, vilket är vad vi vill. Den nya optimala lösningen visas i bild 30-4.

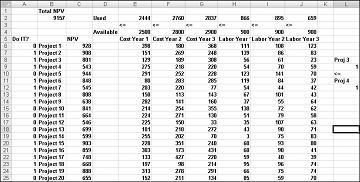
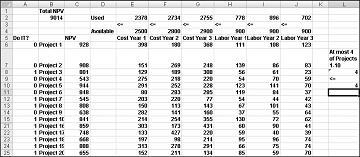
En ny optimal lösning beräknas om du väljer Project 3 innebär att vi också måste välja Project 4. Anta nu att vi bara kan göra fyra projekt mellan projekt 1 till och med 10. (Se kalkylbladet Högst 4 av P1–P10 , som visas i bild 30–5.) I cell L8 beräknar vi summan av de binära värden som är kopplade till Projekt 1 till och med 10 med formeln SUMMA(A6:A15). Sedan lägger vi till villkoret L8<=L10, vilket säkerställer att högst 4 av de första 10 projekten väljs. Den nya optimala lösningen visas i bild 30-5. NETNUVÄRDE har sjunkit till 9,014 miljarder dollar.

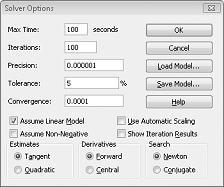
Linjära problemlösare-modeller där vissa eller alla justerbara celler måste vara binära eller heltal är oftast svårare att lösa än linjära modeller där alla justerbara celler tillåts vara bråk. Av denna anledning är vi ofta nöjda med en nästan optimal lösning på ett binärt eller heltal programmering problem. Om din Problemlösar-modell körs under en längre tid kan det vara bra att justera toleransinställningen i dialogrutan Problemlösarens alternativ. (Se bild 30–6.) En toleransinställning på 0,5 % innebär till exempel att Problemlösaren slutar första gången den hittar en genomförbar lösning som ligger inom 0,5 procent av det teoretiska optimala målcellsvärdet (det teoretiska optimala målcellsvärdet är det optimala målvärdet som hittas när de binära och heltalsbegränsningarna utelämnas). Ofta står vi inför ett val mellan att hitta ett svar inom 10 procent av det optimala på 10 minuter eller att hitta en optimal lösning om två veckor av datortid! Standardvärdet för Tolerans är 0,05 %, vilket innebär att Problemlösaren stannar när ett målcellvärde hittas inom 0,05 procent av det teoretiska optimala målcellsvärdet.

1. Ett företag har nio projekt under övervägande. Netnuvärde som läggs till av varje projekt och det kapital som krävs för varje projekt under de kommande två åren visas i följande tabell. (Alla tal är i miljoner.) Till exempel lägger Project 1 till 14 miljoner USD i NETNUVÄRDE och kräver utgifter på 12 miljoner USD under år 1 och 3 miljoner usd under år 2. Under år 1 är 50 miljoner dollar i kapital tillgängligt för projekt, och 20 miljoner dollar är tillgängligt under år 2.

	NETNUVÄRDE	Utgifter för år 1	Utgifter för år 2
Project 1	14	1,2	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	1,2	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	1,2	18	3

• Om vi inte kan genomföra en bråkdel av ett projekt men måste genomföra antingen hela eller inget av ett projekt, hur kan vi maximera NETNUVÄRDE?

• Anta att om Project 4 genomförs måste Projekt 5 genomföras. Hur kan vi maximera NETNUVÄRDE?

• Ett förlag försöker avgöra vilka av 36 böcker det ska publicera i år. Filen Pressdata.xlsx ger följande information om varje bok:

  • Beräknade intäkter och utvecklingskostnader (i tusentals dollar)

  • Sidor i varje bok

  • Huruvida boken är inriktad på en målgrupp av programvaruutvecklare (anges av en 1 i kolumn E)

    Ett förlag kan publicera böcker på upp till 8 500 sidor i år och måste publicera minst fyra böcker riktade till programvaruutvecklare. Hur kan företaget maximera sin vinst?

Den här artikeln är anpassad från Microsoft Office Excel 2007 Data Analysis and Business Modeling av Wayne L. Winston.

Denna klassrumsbok utvecklades från en serie presentationer av Wayne Winston, en välkänd statistiker och affärsprofessor som specialiserat sig på kreativa, praktiska tillämpningar av Excel.