I det här avsnittet beskrivs de olika trendlinjealternativen som är tillgängliga i Office.
Använd den här typen av trendlinje om du vill skapa en anpassad rät linje för enkla uppsättningar av linjära data. Data är linjära om mönstret i deras datapunkter ser ut som en linje. En linjär trendlinje visar att något ökar eller minskar i jämn takt.
En linjär trendlinje använder den här ekvationen för att beräkna minsta kvadratpassningen för en linje:
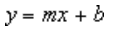
där m är lutningen och b är skärningspunkten.
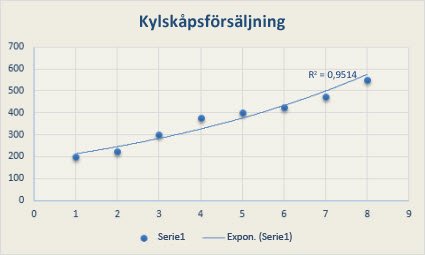
Den linjära trendlinjen här nedanför visar att kylskåpsförsäljningen har ökat konstant under en 8-årsperiod. Observera att R-kvadratvärdet (ett tal från 0 till 1 som visar hur väl trendlinjens uppskattade värden motsvarar de verkliga värdena) är 0,9792, vilket tyder på en god linjär approximation av data.
Trendlinjen visar en anpassad kurva som är användbar när förändringstakten i data inledningsvis är hög och sedan planar ut. En logaritmisk trendlinje kan använda både negativa och positiva värden.
En logaritmisk trendlinje använder den här ekvationen för att beräkna anpassning med hjälp av minsta kvadratmetoden genom punkter:
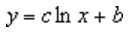
där c och b är konstanter och ln är den naturliga logaritmen.
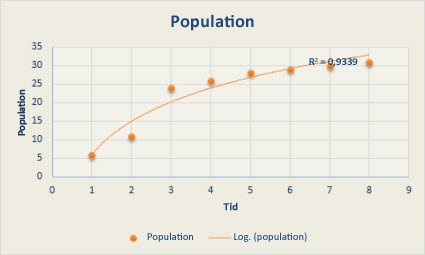
Följande logaritmiska trendlinje visar förutsägelser om en djurpopulations tillväxt inom ett bestämt område där populationen planade ut när utrymmet för djuren minskade. Observera att R-kvadratvärdet är 0,933 vilket är en relativt god anpassning av linjen efter data.
Den här trendlinjen är användbar när dina data fluktuerar. Till exempel när du analyserar vinster och förluster över en stor datamängd. Polynomens ordning kan bestämmas av antalet fluktuationer i data eller av hur många kurvor (kullar och dalar) som förekommer i kurvan. Vanligtvis har en polynom trendlinje av ordningen 2 endast en kulle eller dal, en order 3 har en eller två kullar eller dalar och en order 4 har upp till tre kullar eller dalar.
En polynom eller krökt trendlinje använder den här ekvationen för att beräkna minsta kvadratpassningen genom punkter:
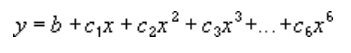
där b och 
Följande polynoma trendlinje av andra ordningen (en topp) visar förhållandet mellan hastighet och bensinförbrukning. Observera att R-kvadratvärdet är 0,979 vilket är nära 1, så linjen är en god linjär approximation av data.
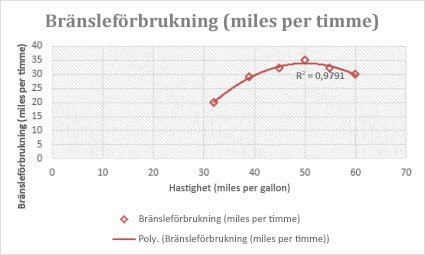
Trendlinjen visar en böjd linje och är användbar för datauppsättningar som jämför mått som ökar med en viss hastighet. Till exempel acceleration av en racerbil med 1-sekundsintervall. Du kan inte skapa en potenstrendlinje om dina data innehåller nollvärden eller negativa värden.
En potenstrendlinje använder den här ekvationen för att beräkna minsta kvadratpassningen genom punkter:
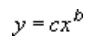
där c och b är konstanter.
Obs!: Det här alternativet är inte tillgängligt om dina data omfattar negativa värden eller nollvärden.
I det följande diagram över sträckenhet exemplet visas sträckan i meter varje sekund. Potenstrendlinjen visar tydligt hastighetsökningen. Observera att R-kvadratvärdet är 0,986 vilket nästan är en perfekt approximation av data.
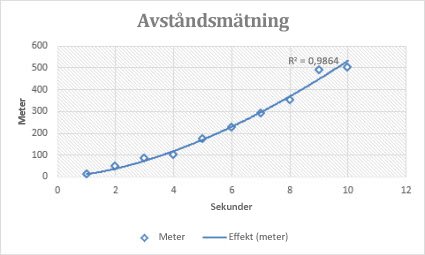
Trendlinjen visar en kurva som är användbar när datavärdena ökar eller minskar i en konsekvent stigande takt. Du kan inte skapa en exponentiell trendlinje om dina data innehåller nollvärden eller negativa värden.
En exponentiell trendlinje använda den här ekvationen för att beräkna minsta kvadratpassningen genom punkter:
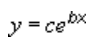
där c och b är konstanter och e är basen för den naturliga logaritmen.
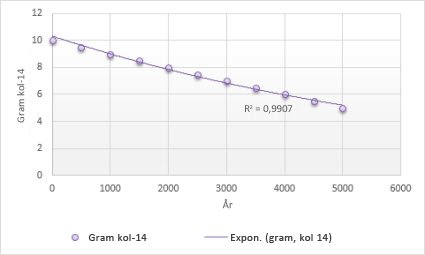
Följande exponentiella trendlinje visar den minskande mängden kol-14 i ett föremål allt eftersom det åldras. Observera att R-kvadratvärdet är 0,990 vilket betyder att linjen nästan är en perfekt approximation av data.
Den här trendlinjen jämnar ut fluktuationer i data för att tydligare visa ett mönster eller en trend. Ett glidande medelvärde använder ett visst antal datapunkter (anges med alternativet Period) vilkas medelvärde används som en punkt i trendlinjen. Om till exempel Period anges till 2 används medelvärdet för de första två datapunkterna som den första punkten i trendlinjen med glidande medelvärde. Medelvärdet för den andra och tredje datapunkten används som den andra punkten i trendlinjen, och så vidare.
En trendlinje med glidande medelvärde använder den här ekvationen:
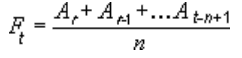
Antalet punkter i en trendlinje med glidande medelvärde motsvarar det totala antalet punkter i en serie minus det antal du anger för perioden.
I ett punktdiagram baseras det glidande medelvärdet på ordningen av x-värden i diagrammet. Du måste kanske sortera x-värdena innan du lägger till ett glidande medelvärde för att få önskat resultat.
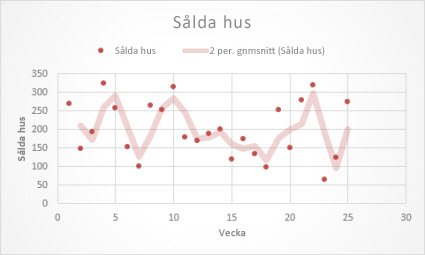
Följande trendlinje med flytande medelvärde visar mönstret i antalet sålda bostäder under en period om 26 veckor.
Viktigt!: Från och med Excel version 2005 justerade Excel hur R 2-värdet beräknas för linjära trendlinjer i diagram där trendlinjeskärningen är inställd på noll (0). Den här justeringen korrigerar beräkningar som gav felaktiga R2-värden och justerar R2-beräkningen med funktionen REGR. Därför kan olika R2-värden visas i diagram som tidigare skapats i tidigare Excel-versioner. Mer information finns i Ändringar av interna beräkningar av linjära trendlinjer i ett diagram.
Behöver du mer hjälp?
Du kan alltid fråga en expert i Excel Tech Community eller få support i Communities.
Se även
Lägga till en trendlinje eller en linje med glidande medelvärde i ett diagram










