Kompleksna analiza podatkov z orodji za analizo

1. Kliknite zavihek Datoteka, Možnosti in nato kategorijo Dodatki.

2. V polju Upravljanje izberite možnost Excelovi dodatki in nato kliknite Pojdi.

   Če uporabljate Excel for Mac, v meniju datoteke odprite Orodja > Excelovi dodatki.

3. V polju Dodatki potrdite potrditveno polje Orodja za analizo in nato kliknite V redu.

   • Če Orodja za analizo niso navedena v oknu Dodatki, ki so na voljo, kliknite Prebrskaj in jih poiščite.

   • Če se prikaže poziv, da orodja za analizo trenutno niso nameščena na vašem računalniku, kliknite Da in jih namestite.

Orodje »Anova« omogoča različne vrste analize variance. Izbira orodja je odvisna od številnih dejavnikov in od števila vzorcev iz populacije, ki jo nameravate testirati.

Anova: en faktor

To orodje izvede preprosto analizo variance podatkov za dva ali več vzorcev. Analiza daje preskus hipoteze, da se vsak vzorec črpa iz iste temeljne porazdelitve verjetnosti glede na alternativno hipotezo, da temeljne verjetnostne porazdelitve niso enake za vse vzorce. Če sta na voljo le dva vzorca, lahko uporabite funkcijo delovnega lista T.PRESKUS. Pri več kot dveh vzorcih ni priročne generalizacije T.Test in namesto tega lahko uporabite model Single Factor Anova.

Anova: dva faktorja s podvajanjem

To orodje za analizo je uporabno, ko je podatke mogoče razvrstiti v dveh različnih dimenzijah. V poskusu na primer za merjenje višine rastlin se rastlinam lahko dajo različne znamke gnojila (na primer A, B, C) in se lahko tudi hranijo pri različnih temperaturah (na primer pri nizkih, visokih). Za vsakega od šestih možnih parov {gnojilo, temperatura} imamo enako število opazovanj višine rastlin. S tem orodjem Anova lahko preskusimo:

• Ali se višine rastlin za različne znamke gnojila izberejo iz iste temeljne populacije? Temperature se pri tej analizi prezrejo.

• Ali se višine rastlin za različne ravni temperature izberejo iz iste temeljne populacije? Znamke gnojil se pri tej analizi prezrejo.

Ali se, glede na ocene za posledice razlik med znamkami gnojil v prvi točki z oznakami in razlikami v temperaturah v drugi točki z oznakami, šest vzorcev, ki predstavlja vse pare vrednosti {gnojilo, temperatura}, izbere iz iste populacije? Alternativna hipoteza je, da so posledice zaradi določenih parov {gnojilo, temperatura} prek in nad razlikami, ki temeljijo samo na gnojilu ali pa samo na temperaturi.

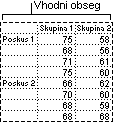
Anova: dva faktorja brez podvajanja

To orodje za analizo je uporabno, ko so podatki razvrščeni v dve različni dimenziji, kot je Two-Factor primeru S replikacijo. Vendar pa se za to orodje predvideva, da obstaja le eno opazovanje za vsak par (na primer vsak par {gnojilo, temperatura} v prejšnjem primeru).

Funkciji CORREL in PEARSON delovnega lista izračunata korelacijski koeficient med dvema merskima spremenljivkama, ko mere vsake spremenljivke opazujete za vsakega od N predmetov. (Katero koli manjkajoče opazovanje za kateri koli predmet povzroči, da bo ta predmet v analizi prezrt.) Orodje za analizo korelacije je še posebej uporabno, ko imate več kot dve merski spremenljivki za vsakega od N predmetov. Priskrbi izhodno tabelo, korelacijsko matriko, ki prikaže vrednost CORREL (ali PEARSON), ki jo uporablja vsak možen par merskih spremenljivk.

Korelacijski koeficient je tako kot kovarianca mera, do katere dve merski spremenljivki »variirata skupaj«. V nasprotju s kovarianco je korelacijski koeficient usmerjen tako, da je njegova vrednost neodvisna od enot, v katerih sta izraženi dve merski spremenljivki. (Če sta dve merski spremenljivki, na primer teža in višina, ostane vrednost korelacijskega koeficienta nespremenjena, če težo pretvorimo iz funtov v kilograme.) Vrednost katerega koli korelacijskega koeficienta mora biti med vključno -1 in 1.

Orodje za korelacijo lahko uporabljate, če želite preučiti vsak par merskih spremenljivk, da ugotovite, ali se ti dve merski spremenljivki nagibata k skupnemu premikanju — se pravi, ali so velike vrednosti ene spremenljivke nagnjene k povezavi z velikimi vrednostmi druge spremenljivke (pozitivna korelacija), ali so majhne vrednosti ene spremenljivke nagnjene k povezavi z velikimi vrednostmi druge spremenljivke (negativna korelacija) ali pa vrednosti obeh spremenljivk sploh nista v sorodu (korelacija blizu 0 (nič)).

Orodji za korelacijo in kovarianco lahko uporabimo v isti nastavitvi, ko v naboru posameznikov opazujete N različnih merskih spremenljivk. Orodji za korelacijo in kovarianco ponudita izhodno tabelo, matriko, ki prikazuje korelacijski koeficient oziroma kovarianco med vsakim parom merskih spremenljivk. Razlika je v tem, da je vrednost korelacijskega koeficienta med vključno -1 in vključno 1. Ustrezna kovarianca nima omejitev. Korelacijski koeficient in kovarianca sta meri, do katerih dve spremenljivki »variirata skupaj«.

Orodje za kovarianco izračuna vrednost funkcije delovnega lista COVARIANCE. P za vsak par merskih spremenljivk. (Neposredna uporaba funkcije COVARIANCE. P namesto orodja za kovarianco je razumna alternativa, če sta na voljo le dve mersko spremenljivki, to je N=2.) Vnos na diagonalno izhodno tabelo orodja za kovarianco v vrstici i, stolpcu i je kovarianca i-te merske spremenljivke sama s seboj. To je le varianca populacije za to spremenljivko, kot jo izračuna funkcija delovnega lista VAR.V redu.

Orodje Kovarianca lahko uporabljate, če želite preučiti vsak par merskih spremenljivk, da ugotovite, ali se ti dve merski spremenljivki nagibata k skupnemu premikanju  — se pravi, ali so velike vrednosti ene spremenljivke nagnjene k povezavi z velikimi vrednostmi druge spremenljivke (pozitivna kovarianca), ali so majhne vrednosti iz ene spremenljivke nagnjene k povezavi z velikimi vrednostmi druge spremenljivke (negativna kovarianca) ali pa vrednosti obeh spremenljivk sploh nista v sorodu (kovarianca blizu 0 (nič)).

Ustvari poročilo o enovariabilni statistiki za podatke v vhodnem obsegu z informacijami o osrednji tendenci in variabilnosti podatkov.

Orodje za analizo Eksponentno glajenje predvidi vrednost glede na napovedi prejšnjega obdobja, ki je prilagojena za napako v tej napovedi. Uporablja konstanto glajenja a, katere velikost določa, koliko se napovedi odzivajo na napake v prejšnjih napovedih.

Izvede dvovzorčni F-test in primerja dve populacijski varianci.

Orodje F-Test lahko na primer uporabite na vzorcih časov plavalnega tekmovanja za vsako od dveh ekip. Orodje priskrbi rezultat preskusa ničelne hipoteze, da ta vzorca prihajata iz porazdelitve z enakimi variancami, proti alternativni hipotezi, da variance niso enake v temeljni porazdelitvi.

Orodje izračuna vrednost »f« F-statistike (ali F-razmerje). Vrednost »f« blizu 1 priskrbi dokaz, da so temeljne variance populacije enake. Če je v izhodni tabeli f < 1, da »P(F <= f) enorepo« verjetnost opazovanja vrednosti F-statistike manj kot »f«, ko so variance populacije enake in da »enorepi kritični F« kritično vrednost, ki je za izbrano raven zaupanja alfa manj kot 1. Če je f > 1, da »P(F <= f) enorepo« verjetnost opazovanja vrednosti F-statistike več kot »f«, ko so variance populacije enake in da »enorepi kritični F« kritično vrednost, ki je za alfo večja kot 1.

Orodje za Fourierjevo analizo rešuje probleme linearnih sistemov in analizira periodične podatke z metodo hitre Fourierjeve transformacije (FFT - Fast Fourier Transform). To orodje podpira tudi inverzne transformacije, ki vrnejo izvirne podatke na podlagi invertiranih transformiranih podatkov.

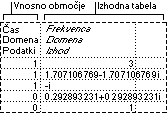
Orodje za analizo Histogram izračuna posamezne in seštevalne frekvence za obseg celic podatkov in predale podatkov. Ustvari tudi podatke za število pogostosti vrednosti v podatkovni množici.

Primer: V razredu z 20 učenci lahko ugotovite porazdelitev ocen po številčnih vrednostih od 1 (nezadostno) do 5 (odlično). Histogramska tabela predstavlja meje številčnih vrednosti ocen in število ocen med najnižjo in trenutno mejo. Tista ocena, ki je najbolj pogosta, se imenuje način podatkov.

Predvideva vrednosti v obdobju napovedi na podlagi povprečne vrednosti spremenljivke čez določeno število prehodnih obdobij. Drseče povprečje daje informacije o smernicah, ki bi jih preprosto povprečje vseh podatkov iz preteklosti zakrilo. Uporabljajte to orodje za predvidevanje obsega prodaje, zalog in drugih smernic. Vsaka napovedana vrednost temelji na formuli:

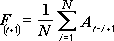
kjer je:

• N število prejšnjih obdobij, ki jih želite vključiti v drseče povprečje

• A j dejanska vrednost ob času j

• F j napovedana vrednost ob času j

Orodje za analizo Generiranje naključnih števil napolni obseg z neodvisnimi naključnimi števili, vzetimi iz ene od več porazdelitev. To orodje lahko uporabljate, če želite pripisati porazdelitev verjetnosti elementom v populaciji. Lahko na primer opišete populacijo telesne višine posameznikov, uporabite normalno porazdelitev ali pa uporabite Bernoullijevo porazdelitev dveh mogočih izidov, če želite opisati populacijo izidov pri metanju kovanca.

Orodje za analizo Rank in Percentile ustvari tabelo, ki vsebuje rang števnih redov in odstotkov posamezne vrednosti v naboru podatkov. Analizirate lahko relativni položaj vrednosti v naboru podatkov. To orodje uporablja funkcije delovnega lista RANK. EQ inPERCENTRANK. INC. Če želite vključiti vezane vrednosti, uporabite RANK. Funkcija EQ , ki obravnava vezane vrednosti kot enake rede, ali pa uporablja RANK.Funkcija AVG , ki vrne povprečni red za vezane vrednosti.

Orodje za analizo Regresija izvede analizo linearne regresije z uporabo metode »najmanjših kvadratov« in množico merskih točk približa premici. To orodje lahko uporabljate za analizo, kako na vrednost ene odvisne spremenljivke vplivajo vrednosti ene ali več neodvisnih spremenljivk.Analizirate lahko, kako na primer vplivajo na atletove dosežke dejavniki, kot so starost, višina in teža. Vsem tem trem dejavnikom lahko pripišete deleže pomembnosti za učinkovitost atleta na podlagi podatkovne množice o učinkovitosti. Nato uporabite rezultat, če želite predvideti zmogljivosti novega atleta, ki ga še niste preskusili.

Orodje za regresijo uporablja funkcijo delovnega lista LINEST.

Orodje za analizo vzorčenja ustvari vzorec iz populacije tako, da vnosni obseg obravnava kot populacijo. Ko je populacija prevelika za obdelavo ali grafikon, lahko uporabite reprezentativen vzorec. Ustvarite lahko tudi vzorec, ki vsebuje samo vrednosti iz določenega dela cikla, če ste po vaši mnenju, da so vhodni podatki občasni. Če na primer vhodni obseg vsebuje podatke o četrtletni prodaji, vzorčenje s periodično stopnjo štirih postavi vrednosti iz istega četrtletja v obseg proizvodnje.

Orodja za analizo dvovzorčnega t-Testa preskušajo enakost sredin populacije, ki temeljijo na vsakem vzorcu. Tri orodja uporabljajo različne domneve: da so variance populacije enake, da variance populacije niso enake in da dva vzorca predstavljata opazovanja pred obdelavo in po njej na istem predmetu.

Za vsa tri spodnja orodja se izračuna t-statistična vrednost, t in je v izhodnih tabelah prikazana kot »t Stat«. Glede na podatke je lahko ta vrednost t negativna ali nenegativna. Ob predpostavki enakopravnih srednjih vrednosti temeljne populacije, če je t < 0, da "P(T <= t) enorepo" verjetnost, da bo opazovana vrednost t-statistike, ki je bolj negativna kot t. Če je >=0, da »P(T <= t) enorepo« verjetnost, da bo opazovana vrednost t-statistike, ki je bolj pozitivna kot t. »t Kritični enorepi« da cutoff vrednost, tako da je verjetnost opazovanja vrednosti t-statistike, ki je večja ali enaka »t Kritični enorepi« alfa.

»P(T <= t) dvorepi« da verjetnost, da bo opazovana vrednost t-statistike, katere absolutna vrednost je večja kot t. »Dvorepi kritični P« da zmanjšano vrednost, tako da verjetnost opazovanja t-statistike, katere absolutna vrednost je večja kot »Dvorepi kritični P«, alfa.

t-Test: v paru z dvema vzorcema za aritmetične sredine

Preskus v paru lahko uporabite, ko imate v vzorcih naravno združevanje opazovanj v pare, na primer ko je vzorčna skupina preskušena dvakrat — pred poskusom in po njem. To orodje za analizo in njegova formula izvajata dvovzorčni študentov t-Test v paru, da določi, ali so opazovanja pred obdelavo in po njej prišla iz porazdelitev z enakimi sredinami populacije. Ta oblika t-Testa ne predvideva, da sta varianci obeh populacij enaki.

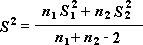
t-Test: z dvema vzorcema z upoštevanjem enakih varianc

To orodje za analizo izvede dvovzorčni študentov t-Test. Ta oblika t-Testa predpostavlja, da sta ti množici podatkov prišli iz porazdelitev z enakimi variancami. To imenujemo tudi homoskedastični t-Test. Te t-Teste lahko uporabite, da ugotovite, ali sta ta vzorca prišla iz porazdelitev z enakimi sredinami populacije.

t-Test: z dvema vzorcema z upoštevanjem neenakih varianc

To orodje za analizo izvede dvovzorčni študentov t-Test. Ta oblika t-Testa predvideva, da sta bila ta nabora podatkov iz porazdelitev z neenakimi variancami. To se imenuje heteroskedastični t-Test. Kot pri prejšnjih primerih z enakimi variancami lahko uporabite ta t-Test, da ugotovite, ali sta vzorca prišla iz porazdelitev z enakimi srednjimi sredstvi populacije. Ta preskus uporabite, ko sta v dveh vzorcih različna predmeta. Preskus v paru, opisan v spodnjem primeru, uporabite, če obstaja en sam niz predmetov in dva vzorca predstavljata meritve za vsak predmet pred obdelavo in po njem.

Formula, ki jo program uporablja za ugotavljanje statistične vrednosti preskusa t, je:

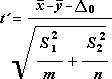
Ta formula se uporablja za izračun prostostnih stopenj, df. Ker rezultat izračuna običajno ni celo število, je vrednost df zaokrožena na najbližje celo število, da se dobi kritična vrednost iz t tabele. Funkcija Excelovega delovnega lista T.TEST uporablja izračunano vrednost df brez zaokroževanja, ker je mogoče izračunati vrednost za T.TEST z neintegerjem df. Zaradi teh različnih pristopov k določanju stopenj prostosti, rezultati T.Test in to orodje t-Test se bosta razlikovala v primeru neenakih odmikov.

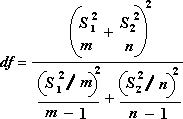
Z-Test: Z-Test z dvema vzorcema za orodje za analizo srednjih vrednosti izvedeta dva vzorčna z-Testa za srednji vrednosti z znanimi variancami. To orodje se uporablja za preskus ničelne hipoteze, da ni razlike med dvema srednjima točkama populacije glede na enostranske ali dvostranske nadomestne hipoteze. Če variance niso znane, funkcija delovnega lista Z.Namesto tega uporabite TEST.

Ko uporabljate orodje z-Test, bodite previdni pri razumevanju rezultata. »P(Z <= z) enorepo« je dejansko P(Z >= ABS(z)), verjetnost z-vrednosti, ki je dlje od 0 v isti smeri kot opazovana z-vrednost, ko ni razlike med sredinami populacije. »P(Z <= z) dvorepo« je dejansko P(Z >= ABS(z) ali Z <= -ABS(z)), verjetnost z-vrednosti, ki je dlje od 0 v kateri koli smeri kot opazovana z-vrednost, ko ni razlike med sredinami populacije. Dvorepi rezultat je samo enorepi rezultat, pomnožen z 2. Orodje z-Test lahko uporabite tudi v primerih, kjer je ničelna hipoteza, da je za razliko med dvema sredinama populacije določena neničelna vrednost. Ta preskus lahko na primer uporabite, če želite ugotoviti razlike v zmogljivostih dveh modelov osebnih vozil.