В этой статье описаны синтаксис формулы и использование функции ZТЕСТ в Microsoft Excel.
Возвращает одностороннее значение вероятности z-теста. Для заданного гипотетического среднего генеральной совокупности (μ0) функция ZТЕСТ возвращает вероятность того, что выборочное среднее будет больше среднего значения множества рассмотренных данных (массива), называемого также средним значением наблюдаемой выборки.
Сведения об использовании функции ZТЕСТ в формуле для вычисления двустороннего значения вероятности см. ниже в разделе "Замечания".
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция Z.ТЕСТ.
Синтаксис
ZТЕСТ(массив;x;[сигма])
Аргументы функции ZТЕСТ описаны ниже.
-
Массив Обязательный. Массив или диапазон данных, с которыми сравнивается x.
-
X Обязательный. Проверяемое значение.
-
Сигма Необязательный. Известное стандартное отклонение генеральной совокупности. Если этот аргумент опущен, используется стандартное отклонение выборки.
Замечания
-
Если массив пуст, то функция ZТЕСТ возвращает значение ошибки #Н/Д.
-
Функция ZТЕСТ вычисляется следующим образом. Если аргумент "сигма" не опущен:
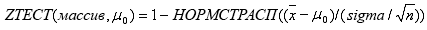
Если аргумент "сигма" опущен:

где x — выборочное среднее значение СРЗНАЧ(массив); s — выборочное среднеквадратичное отклонение СТАНДОТКЛОН(массив); n — число наблюдений СЧЁТ(массив).
-
Функция ZТЕСТ представляет вероятность того, что выборочное среднее будет больше среднего значения множества рассмотренных данных СРЗНАЧ(массив) при значении математического ожидания, равном μ0. Исходя из симметрии нормального распределения, если СРЗНАЧ(массив) < μ0, функция ZТЕСТ вернет значение больше 0,5.
-
Приведенную ниже формулу Microsoft Excel можно использовать для вычисления двустороннего значения вероятности того, что выборочное среднее будет отличаться от μ0 (в любом направлении) больше, чем СРЗНАЧ(массив), при математическом ожидании генеральной совокупности, равном μ0.
=2 * МИН(ZТЕСТ(массив;μ0;сигма), 1 - ZТЕСТ(массив;μ0;сигма)).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Формула |
Описание (результат) |
Результат |
|
=ZТЕСТ(A2:A11;4) |
Одностороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 4 (0,090574) |
0,090574 |
|
=2 * МИН(ZТЕСТ(A2:A11;4); 1 - ZТЕСТ(A2:A11;4)) |
Двустороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 4 (0,181148) |
0,181148 |
|
=ZТЕСТ(A2:A11;6) |
Одностороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 6 (0,863043) |
0,863043 |
|
=2 * МИН(ZТЕСТ(A2:A11;6); 1 - ZТЕСТ(A2:A11;6)) |
Двустороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 6 (0,273913) |
0,273913 |










