Использование решателя для бюджетирования капитала

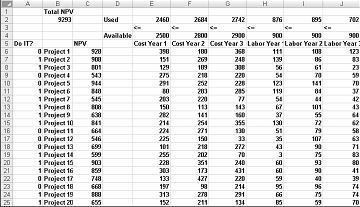
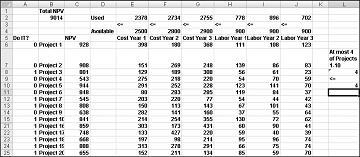
Большинство корпораций хотят осуществлять проекты, которые обеспечивают наибольшую чистую стоимость (NPV), при условии ограниченности ресурсов (как правило, капитала и рабочей силы). Предположим, что компания по разработке программного обеспечения пытается определить, какой из 20 проектов программного обеспечения она должна предпринять. NPV (в миллионах долларов), внесенный каждым проектом, а также капитал (в миллионах долларов) и количество программистов, необходимых в течение каждого из следующих трех лет, приведены на листе Базовая модель в файле Capbudget.xlsx, который показан на рис. 30-1 на следующей странице. Например, проект 2 дает 908 миллионов долларов. Это требует $ 151 млн в течение 1 года, $ 269 млн в течение года 2, и $ 248 млн в течение года 3. Проект 2 требует 139 программистов в течение года 1, 86 программистов в течение года 2 и 83 программиста в течение года 3. Ячейки E4:G4 показывают капитал (в миллионах долларов), доступный в течение каждого из трех лет, а ячейки H4:J4 указывают, сколько программистов доступно. Например, в год доступно от 1 до $2,5 млрд капитала и 900 программистов.

Компания должна решить, следует ли выполнять каждый проект. Предположим, что мы не можем выполнить часть программного проекта; Например, если мы выделим 0,5 необходимых ресурсов, у нас будет неработающая программа, которая принесет нам доход в размере 0 долл. США!

Хитрость при моделировании ситуаций, в которых вы делаете или не делаете что-то, заключается в использовании двоичных изменяющихся ячеек. Двоичная изменяющаяся ячейка всегда равна 0 или 1. Если двоичная изменяющаяся ячейка, соответствующая проекту, равна 1, мы делаем проект. Если двоичная изменяющаяся ячейка, соответствующая проекту, равна 0, проект не выполняется. Вы настроите Средство решения для использования диапазона двоичных изменяющихся ячеек путем добавления ограничения. Выберите изменяющиеся ячейки, которые вы хотите использовать, а затем выберите в списке в диалоговом окне Добавление ограничения.

В этом контексте мы готовы решить проблему выбора проекта программного обеспечения. Как и в случае с моделью Решателя, мы начинаем с определения целевой ячейки, изменяющихся ячеек и ограничений.

• Целевая ячейка. Мы максимально увеличиваем NPV, создаваемый выбранными проектами.

• Изменение ячеек. Мы ищем 0 или 1 двоичную изменяющуюся ячейку для каждого проекта. Я разместил эти ячейки в диапазоне A6:A25 (и назвал диапазон doit). Например, 1 в ячейке A6 указывает, что мы берем проект 1; значение 0 в ячейке C6 указывает, что мы не предпринимаем проект 1.

• Ограничения целостности. Мы должны убедиться, что для каждого года t (t=1, 2, 3), год t используемый капитал меньше или равен год t капитала, доступный, и год t используемый труд меньше или равен году t доступной рабочей силы.

Как видите, наш лист должен вычислить для любого выбора проектов NPV, капитал, используемый ежегодно, и программистов, используемых каждый год. В ячейке B2 я использую формулу SUMPRODUCT(doit,NPV) для вычисления общего NPV, созданного выбранными проектами. (Имя диапазона NPV относится к диапазону C6:C25.) Для каждого проекта с 1 в столбце A эта формула выбирает NPV проекта, а для каждого проекта с 0 в столбце A эта формула не получает NPV проекта. Таким образом, мы можем вычислить NPV всех проектов, а наша целевая ячейка является линейной, так как вычисляется путем суммирования терминов, следующих за формой (изменяющаяся ячейка)*(константой). Аналогичным образом, я вычисляю капитал, используемый каждый год, и труд, используемый каждый год, путем копирования из E2 в F2:J2 формулу SUMPRODUCT(doit,E6:E25).

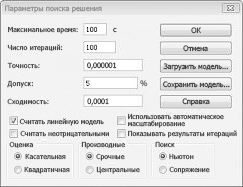
Теперь я заполнию диалоговое окно Параметры решателя, как показано на рис. 30-2.

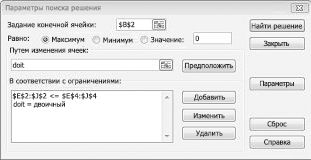
Наша цель — максимально увеличить NPV выбранных проектов (ячейка B2). Наши изменяющиеся ячейки (диапазон с именем doit) — это двоичные изменяющиеся ячейки для каждого проекта. Ограничение E2:J2<=E4:J4 гарантирует, что в течение каждого года используемый капитал и труд меньше или равен капиталу и труду, доступным. Чтобы добавить ограничение, которое делает изменяющиеся ячейки двоичными, я нажимаю кнопку Добавить в диалоговом окне Параметры решателя, а затем в списке в центре диалогового окна выберите Bin (Bin) из списка. Должно появиться диалоговое окно Добавление ограничения, как показано на рис. 30-3.

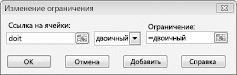
Наша модель является линейной, так как целевая ячейка вычисляется как сумма терминов, имеющих форму (изменяющаяся ячейка)*(констант), а ограничения использования ресурсов вычисляются путем сравнения суммы (изменяющихся ячеек)*(константы) с константой.

Заполнив диалоговое окно Параметры решателя, нажмите кнопку Решить, и у нас есть результаты, показанные ранее на рис. 30-1. Компания может получить максимальный NPV в размере $9,293 млн ($9,293 млрд), выбрав Проекты 2, 3, 6–10, 14–16, 19 и 20.

Иногда модели выбора проекта имеют другие ограничения. Например, предположим, что при выборе проекта 3 необходимо также выбрать Проект 4. Так как наше текущее оптимальное решение выбирает Проект 3, но не Проект 4, мы знаем, что текущее решение не может оставаться оптимальным. Чтобы решить эту проблему, просто добавьте ограничение на то, что двоичная изменяющаяся ячейка для Project 3 меньше или равна двоичной изменяющейся ячейке для проекта 4.

Этот пример можно найти на листе If 3 then 4 в файле Capbudget.xlsx, как показано на рис. 30-4. Ячейка L9 ссылается на двоичное значение, связанное с Проектом 3, а ячейка L12 — на двоичное значение, связанное с Проектом 4. При добавлении ограничения L9<=L12, если выбран параметр Project 3, L9 равен 1, а ограничение L12 (двоичный файл Проекта 4) равно 1. Наше ограничение также должно оставить двоичное значение в изменяющейся ячейке Project 4 без ограничений, если мы не выбрали Проект 3. Если не выбрать Project 3, L9 будет равен 0, а наше ограничение позволяет двоичному файлу Project 4 быть равным 0 или 1, что нам нужно. Новое оптимальное решение показано на рис. 30-4.

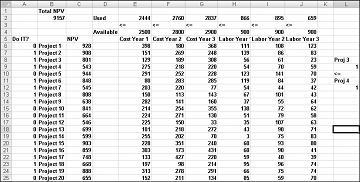
Новое оптимальное решение вычисляется, если при выборе проекта 3 необходимо также выбрать Проект 4. Теперь предположим, что мы можем выполнить только четыре проекта из числа проектов 1–10. (См . лист не более 4 из P1–P10 , показанный на рис. 30–5.) В ячейке L8 вычисляется сумма двоичных значений, связанных с Проектами 1–10, с помощью формулы СУММ(A6:A15).. Затем мы добавим ограничение L8<=L10, которое гарантирует, что выбрано не более 4 из первых 10 проектов. Новое оптимальное решение показано на рис. 30-5. NPV упал до $9,014 млрд.

Модели линейного решателя, в которых некоторые или все изменяющиеся ячейки должны быть двоичными или целыми числами, обычно сложнее решать, чем линейные модели, в которых все изменяющиеся ячейки могут быть дробями. По этой причине мы часто удовлетворены практически оптимальным решением двоичной или целочисленной задачи программирования. Если модель Решателя работает в течение длительного времени, можно настроить параметр "Допустимость" в диалоговом окне Параметры решателя. (См. рис. 30-6.) Например, значение допустимости 0,5 % означает, что решатель остановится при первом поиске возможного решения, которое находится в пределах 0,5 процента от теоретически оптимального значения целевой ячейки (теоретически оптимальное целевое значение является оптимальным целевым значением, найденным при опущении двоичных и целых чисел). Часто мы сталкиваемся с выбором между поиском ответа в течение 10 процентов от оптимального за 10 минут или поиском оптимального решения в течение двух недель компьютерного времени! Значение допуска по умолчанию составляет 0,05 %, что означает, что решатель останавливается при поиске значения целевой ячейки в пределах 0,05 % от теоретически оптимального значения целевой ячейки.

1. Компания имеет девять проектов на рассмотрении. В следующей таблице показано значение NPV, добавляемое каждым проектом, и капитал, необходимый для каждого проекта в течение следующих двух лет. (Все цифры в миллионах.) Например, проект 1 добавит 14 миллионов долларов США в NPV и потребует расходов в размере 12 миллионов долларов США в течение 1 года и 3 миллиона долларов США в течение 2 года. В течение 1 года для проектов доступно $50 млн капитала, а в течение 2-го года — $20 млн.

	NPV	Расходы на год 1	Расходы на год 2
Проект 1	14	12	3
Проект 2	17	54	7
Проект 3	17	6	6
Проект 4	15	6	2
Проект 5	40	30	35
Проект 6	12	6	6
Проект 7	14	48	4
Проект 8	10	36	3
Проект 9	12	18	3

• Если мы не можем взять на себя часть проекта, но должны выполнить либо все, либо ни один из проектов, как мы можем максимизировать NPV?

• Предположим, что если выполняется проект 4, необходимо выполнить проект 5. Как можно максимизировать NPV?

• Издательская компания пытается определить, какие из 36 книг она должна опубликовать в этом году. Файл Pressdata.xlsx содержит следующие сведения о каждой книге:

  • Прогнозируемые доходы и затраты на разработку (в тысячах долларов)

  • Страницы в каждой книге

  • Ориентирована ли книга на аудиторию разработчиков программного обеспечения (указывает 1 в столбце E)

    Издательская компания может опубликовать книги на общую сумму до 8500 страниц в этом году и должна опубликовать по крайней мере четыре книги, ориентированные на разработчиков программного обеспечения. Как компания может максимизировать свою прибыль?

Эта статья была адаптирована на основе microsoft Office Excel 2007 Data Analysis and Business Modeling by Wayne L. Winston.

Эта книга в стиле аудитории была разработана из серии презентаций Уэйном Уинстоном, известным статистиком и бизнес-профессором, который специализируется на творческих, практических применениях Excel.