В этой статье обсуждается использование надстройки Microsoft Excel "Решение", которая позволяет анализировать "что если" для определения оптимального сочетания продуктов.
Как определить ежемесячный набор продуктов, который позволяет повысить прибыльность?
Компаниям часто требуется определять количество каждого продукта, который будет создаваться ежемесячно. В простейшей форме проблема в наборе продуктов состоит в том, как определить объем каждого продукта, который должен быть произведен в течение месяца, чтобы максимально увеличить прибыль. Сочетание продуктов обычно должно соответствовать следующим ограничениям:
-
Сочетание продуктов не может использовать больше ресурсов, чем доступно.
-
Потребность в каждом продукте ограничена. В течение месяца мы не можем создать больше продукции, чем это диктует потребность в продукции, так как в нее нагребают лишние продукты (например, избежаемый продукт).
Теперь рассмотрим пример проблемы со сочетанием продуктов. Решение этой проблемы можно найти в файле Prodmix.xlsx, как показано на рисунке 27-1.
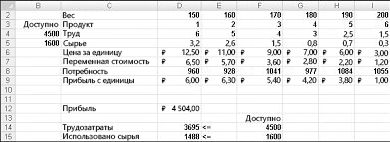
Предположим, что мы работаем в компании, которая производит шесть различных продуктов на своем заводе. Для производства каждого продукта требуются трудовые и необработанные материалы. В строке 4 на рисунке 27-1 показано количество часов труда, необходимое для получения фунта каждого товара, а в строке 5 — фунт необработанных материалов, необходимых для получения фунта каждого товара. Например, для получения фунта продукта 1 требуется 6 часов труда и 3,2 фунта неотработанных материалов. Цена за фунт для каждого фунта задается в строке 6, цена за единицу за фунт — в строке 7, а доход за фунт — в строке 9. Например, товар 2 продается по 11,00 долларов США за фунт, за единицу стоит 5,70 долларов США за фунт и вклад в сумму 5,30 долларов США за фунт. Запрос за месяц для каждого подмайки выдается в строке 8. Например, потребность в продукте 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов необработанных материалов. Как эта компания может максимально увеличить ежемесячную прибыль?
Если бы нам не было известно ничего о надстройке Excel "Решение", мы могли бы решить эту проблему, построив на этом листах данные о прибылях и использовании ресурсов, связанных с этим сочетанием продуктов. Затем мы использовали пробные и ошибки, чтобы оптимизировать прибыль, не используя при этом больше ресурсов и необработанных материалов, чем доступно, и не изменяя при этом лишние продукты. Над решением этой процедуры мы используем только пробную стадию с ошибкой. По сути, "Поиск решения" — это механизм оптимизации, который безукоризненно выполняет поиск по пробным версиям и ошибкам.
Ключ к решению этой проблемы — эффективное вычисление использования ресурсов и прибыли, связанных с любым сочетанием продуктов. Для этого важно использовать функцию СУММПРОИDUCT. Функция СУММПРОИCT перемножает соответствующие значения в диапазонах ячеев и возвращает сумму этих значений. Каждый диапазон ячеок, используемый в оценке СУММПРОИДУCT, должен иметь одинаковые размеры, что подразумевает, что можно использовать суммпроидуц с двумя строками или двумя столбцами, но не с одной строкой и столбцом.
В качестве примера использования функции СУММПРОИПР в нашем примере мы постараемся вычислить использование ресурсов. Трудоемкие труды вычисляются по
(Количество трудовых единиц, использованных для одного фунта воды в секунду)*(1 фунт 1, произведено)+ (Трудоемка, используемая для одного фунта валюты 2)*(2 фунта, произведенного) + ... (Трудоемка, используемая для одного фунта валюты 6)*(6 фунтов в секунду)
Мы могли бы более утомительным образом вычислять использование труда, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Кроме того, использование необработанных материалов можно вычислять как D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на таблицу для шести продуктов отнимает много времени. Представьте, сколько времени займет работа с компанией, которая производит, например, 50 продуктов на своем заводе. Гораздо проще вычислять трудоемкие и необработанные данные, скопируя из D14 в D15 формулу СУММПРОИДУCT($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш рабочий процесс), но гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, чтобы при копировании формулы все равно записать сочетание продуктов из строки 2. Формула в ячейке D15 вычисляет использование необработанных материалов.
Аналогичным образом прибыль определяется с помощью
(Доход от 1 дохода на фунт)*(1 фунт произведен) + (Доход от 2 дохода на фунт)*(2 фунта произведено) + ... (6 доход на фунт)*(произведено 6 фунтов)
Доход легко вычисляется в ячейке D12 с помощью формулы СУММПРОИКТ(D9:I9;$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для всех продуктов.
-
Целевая ячейка. Наша цель — максимально увеличить прибыль (вычисленную в ячейке D12).
-
Изменяя ячейки. Количество фунта, произведенного каждым продуктом (в диапазоне ячеок D2:I2)
-
Ограничения. В этом примере есть следующие ограничения:
-
Не используйте больше трудовых или необработанных материалов, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
-
Не выполыв при этом больше средств, чем нужно. Это значит, что значения в ячейках D2:I2 (фунта, произведенного для каждого пациента) должны быть меньше или равны требованию для каждого пациента (в ячейках D8:I8).
-
Мы не можем привести к отрицательным последствиям любых проблем с наркотиками.
-
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в "Найти решение". Все, что вам нужно сделать, — это нажать кнопку "Найти решение", чтобы найти набор товаров, который максимально увеличить прибыль!
Для начала на вкладке "Данные" в группе "Анализ" нажмите кнопку "Найти решение".
Примечание: Как объяснялось в главе 26 "Введение в оптимизацию с помощью надстройки Excel "Решение", надстройка "Решение" устанавливается с помощью кнопки Microsoft Office, а затем параметров Excel и надстройки. В списке "Управление" щелкните "Надстройки Excel", выберите поле "Найти решение" и нажмите кнопку "ОК".
Появится диалоговое окно "Параметры решения", как показано на рисунке 27–2.
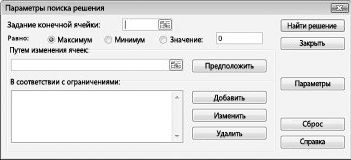
Щелкните поле "Установить целевую ячейку" и выберите ячейку прибыли (ячейка D12). Щелкните поле "Изменяя ячейки", а затем найдите диапазон D2:I2, содержащий количество отсюдоха каждого пациента. Диалоговое окно будет выглядеть как "Рисунок 27-3".
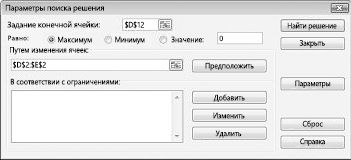
Теперь можно добавить ограничения в модель. Нажмите кнопку "Добавить". На рисунке 27–4 показано диалоговое окно "Добавить ограничение".
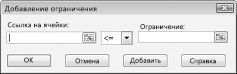
Чтобы добавить ограничения использования ресурсов, щелкните поле "Ссылка на ячейку" и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле ограничения, а затем выберите диапазон ячеев F14:F15. Диалоговое окно "Добавить ограничение" должно выглядеть так: "Рисунок 27-5".
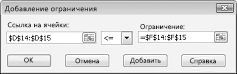
Теперь, когда "Найти решение" пытается использовать другие значения для изменяющихся ячеек, будут учитываться только сочетания, которые удовлетворяют как D14<=F14 (трудоемка меньше или равна доступной работе), так и D15<=F15 (используемый необработаный материал меньше или равен доступному неоцененному). Нажмите кнопку "Добавить", чтобы ввести ограничения по запросу. Заполните поле в диалоговом окне "Добавить ограничение", как показано на рисунке 27–6.
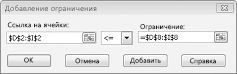
Добавление этих ограничений гарантирует, что при попытках "Найти решение" для изменяемого значения ячейки будут учитываться только сочетания, которые удовлетворяют следующим параметрам:
-
D2<=D8 (количество произведенного средства 1 не превышает потребность в этом средстве)
-
E2<=E8 (количество произведенного средства 2 не превышает или равно запросу на доступ к более 2).
-
F2<=F8 (количество произведенного средства 3 не превышает потребность в этом средстве)
-
G2<=G8 (количество произведенного средства 4 не превышает или равно запросу на доступ к наркотиками 4)
-
H2<=H8 (количество произведенного средства 5 не превышает или равно запросу на доступ к более 5).
-
I2<=I8 (количество произведенного средства 6 не превышает потребность в этом средстве)
В диалоговом окне "Добавить ограничение" нажмите кнопку "ОК". Окно "Решение" должно выглядеть так: "Рисунок 27-7".
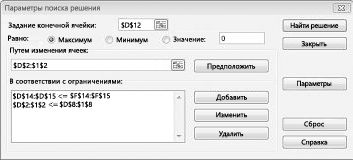
В диалоговом окне "Параметры решения" введите ограничение на то, что изменяющиеся ячейки не должны быть отрицательными. Нажмите кнопку "Параметры" в диалоговом окне "Параметры решения". Проверьте окне "Предполагаемая линейная модель" и "Нео отрицательная", как показано на рисунке 27–8 на следующей странице. Нажмите кнопку "ОК".
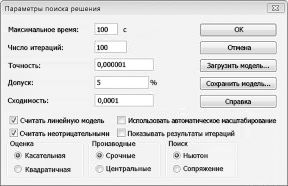
При проверке значения "Предположим, неохожим" над решением будут учитываться только сочетания изменяющихся ячеек, в которых каждая из изменяющихся ячеек принимает нео отрицательное значение. Мы проверили поле "Предполагаемая линейная модель", так как проблема с сочетанием продуктов — это особый тип решения, называемый линейной моделью. По сути, модель "Поиск решения" является линейной в следующих условиях:
-
Целевая ячейка вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа).
-
Каждое ограничение соответствует "требованиям к линейной модели". Это означает, что каждое ограничение вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой.
Почему эта проблема "Поиск решения" линейный? Целевая ячейка (прибыль) вычисляется как
(Доход от 1 дохода на фунт)*(1 фунт произведен) + (Доход от 2 дохода на фунт)*(2 фунта произведено) + ... (6 доход на фунт)*(произведено 6 фунтов)
Эта вычисление вычисляется по шаблону, в котором вычисляется значение конечной ячейки путем с суммирования терминов формы (изменяемой ячейки)*(константа).
Наше ограничение на работу вычисляется путем сравнения значения, полученного из (Количество, используемого в фунте по 1)*(1 фунта влияния) + (Количество, используемого для одного фунта в фунте до 2)*(Фунт 2, полученный в качестве 2 фунта)+ (Трудоемкие мыed per pound of Drug 6)*(Pound 6 pound produced) to the labor available.
Следовательно, ограничение трудоемких ресурсов вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой. Ограничение трудоемких ресурсов и ограничение в необработанных материалах отвечают требованиям к линейной модели.
Наши ограничения запроса принимают форму
(От 1 досье 1)<=(Потребность в наркотиками 1) (От 2 досье 2)<=(Потребность в наркотиками 2) § (от 6 досье 6)<=(Потребность в наркотиками 6)
Каждое ограничение запроса также соответствует требованию к линейной модели, поскольку каждое из них вычисляется путем свести вместе условия формы (изменяемая ячейка)*(константа) и сравнить суммы с константой.
Если вы показываете, что модель нашего продукта является линейной, почему это важно?
-
Если модель "Поиск решения" является линейной и выбран вариант "Предположим, линейный режим", "Поиск решения" гарантирован, что будет найдено оптимальное решение для модели "Поиск решения". Если модель "Поиск решения" не линейный, "Поиск решения" может не найти оптимальное решение.
-
Если модель "Поиск решения" является линейной и выбран вариант "Предполагаемая линейная модель", то для поиска оптимального решения модели используется очень эффективный алгоритм (метод простого решения). Если модель "Поиск решения" является линейной и не выбран вариант "Предполагаемая линейная модель", "Поиск решения" использует очень неэффективный алгоритм (метод ОГР2), что может затруднить поиск оптимального решения модели.
После нажатия кнопки "ОК" в диалоговом окне "Параметры решения" вернимся в главное диалоговое окно "Решение", показанное ранее на рисунке 27–7. При нажатии кнопки "Поиск решения" "Поиск решения" вычисляет оптимальное решение (если оно существует) для модели микса продуктов. Как было сказано в главе 26, оптимальным решением для модели набора продуктов является набор изменяемых значений ячеок (фунта, произведенного каждым продуктом), который позволяет максимально увеличить прибыль в наборе всех возможных решений. В этом же, целесообразное решение — это набор изменяющихся значений ячеок, удовлетворяющий всем ограничениям. Изменяющиеся значения ячеок, показанные на рисунке 27–9, являются допустимым решением, поскольку все производственные уровни неоценимы, производственные уровни не превышают потребность, а использование ресурсов не превышает доступных ресурсов.
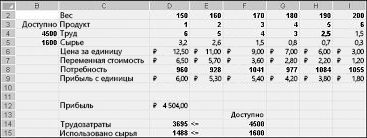
Изменяемые значения ячеек, показанные на рисунке 27–10 на следующей странице, являются неизменяемым решением по следующим причинам:
-
Мы выпускаем больше 5, чем за него требуются.
-
Мы используем больше трудоемких ресурсов, чем доступно.
-
Мы используем больше необработанных материалов, чем доступно.
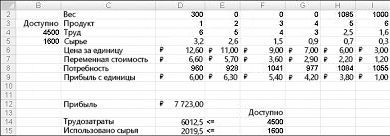
Нажав кнопку "Поиск решения", "Поиск решения" быстро найдет оптимальное решение, показанное на рисунке 27–11. Вам нужно выбрать "Сохранить решение для решения проблемы", чтобы сохранить оптимальные значения решения на работе.

Наша организация, которая занимается наркотиками, может увеличить ежемесячную прибыль в размере 6 625,20 долларов США, выполив 596,67 фунта 4, 1084 фунта для подавлили 5 рублей и ни одного другого фунта! Мы не можем определить, можно ли достичь максимальной прибыли в 6 625,20 долларов США другими способами. Все, что мы можем быть уверены, что из-за ограниченных ресурсов и требований в этом месяце нельзя внести больше 6 627,20 долларов США.
Предположим, что потребность в каждом продукте должна быть выполнены. (См. таблицу "Нет реального решения" в Prodmix.xlsx.) Затем нам нужно изменить ограничения по запросу с D2:I2<=D8:I8 на D2:I2>=D8:I8. Для этого откройте "Решение", выберите ограничение D2:I2<=D8:I8 и нажмите кнопку "Изменить". Появится диалоговое окно "Изменение ограничения", показанное на рисунке 27–12.
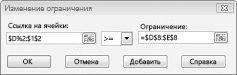
Выберите >=, а затем нажмите кнопку "ОК". Теперь над решением можно изменить только значения ячеок, которые соответствуют всем запросам. При нажатии кнопки "Найти решение" отобразилось сообщение "Поиск решения не удалось найти целесообразное решение". Это сообщение не означает, что мы допустили ошибку в модели, а о том, что из-за ограниченных ресурсов мы не сможем выполнить потребность во всех товарах. Надстройка "Решение" просто сообщает нам, что если мы хотим удовлетворить потребность в каждом продукте, нам нужно добавить больше труда, дополнительных необработанных материалов или и тех, и других.
Давайте посмотрим, что произойдет, если разрешить неограниченную потребность в каждом продукте и разрешить отрицательные количества каждого товара. (Эта проблема возникает в области "Набор значений не сходится" на Prodmix.xlsx.) Чтобы найти оптимальное решение в этой ситуации, откройте "Поиск решения", нажмите кнопку "Параметры" и откроем поле "Неохритимые". В диалоговом окне "Параметры решения" выберите ограничение запроса D2:I2<=D8:I8, а затем нажмите кнопку "Удалить", чтобы удалить это ограничение. При нажатии кнопки "Найти решение" возвращается сообщение "Установить значение ячейки не сходится". Это сообщение означает, что если нужно развернуть целевую ячейку (как в нашем примере), существуют допустимые решения, в том числе и для суммарных значений целевых ячеок. (Если целевая ячейка должна быть свернута, сообщение "Установить значения ячейки не сходятся" означает, что существуют возможные решения с небольших целевых значений, заверяемого в третейском деле.) В нашем случае, разрешив негативное производство в случае злоупотреблений, мы фактически создадим ресурсы, которые можно использовать для вывода в произвольное количество других средств. С учетом нашего неограниченного запроса это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечно. Если вы видите сообщение "Установить значения не сходятся", это означает, что в модели есть ошибка.
-
Предположим, в нашей компании в течение часа можно приобретать до 500 часов работы на 100 рублей больше, чем за текущие трудоемкие расходы. Как максимально увеличить прибыль?
-
На изготовителе микросхем четыре технических специалиста (A, B, C и D) выпускают три продукта ("Товары 1", "2" и "3"). В этом месяце изготовитель микросхемы может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Специалист А может делать только продукты 1 и 3. Специалист Б может делать только продукты 1 и 2. Специалист C может сделать только продукт 3. Специалист D может сделать только продукт 2. Для каждого произведенного товара внести следующую прибыль: Товар 1; 600 рублей; Товар 2; 7000 рублей; и товар 3, 1000 рублей. Время (в часах) каждого технических специалиста, необходимое для производства продукта, должно быть следующим:
Продукт
Специалист А
Специалист Б
Специалист C
Специалист Д
1
2
2,5
Не удается сделать
Не удается сделать
2
Не удается сделать
3
Не удается сделать
3,5
3
3
Не удается сделать
4
Не удается сделать
-
Каждый специалист может работать до 120 часов в месяц. Как изготовитель микросхем может максимально увеличить ежемесячную прибыль? Предположим, что можно получить лишь дробное количество единиц.
-
Компьютерный завод производит мыши, клавиатуры и игровые joysticks. Доход за единицу, за единицу трудоемких ресурсов, ежемесячная потребность и за единицу машинного времени даются в следующей таблице:
Мыши
Клавиатуры
Joysticks
Прибыль/единица
8 $
11 $
9 $
Использование трудов и единицы
0,2 часа
0,3 часа
0,24 часа
Машинное время/единица
0,04 ч
0,055 ч.
0,04 ч
Ежемесячный запрос
15 000
27,000
11,000
-
Каждый месяц доступно 13 000 часов труда и 3000 часов машинного времени. Как изготовитель может максимально увеличить ежемесячный взнос в прибыль от растения?
-
Допустим, необходимо устранить проблему с этой проблемой при условии, что должны быть выполнены минимальные требования к 200 единицам для каждого из них.
-
Он делает ромбовидные ромбои, окаймлы и затейные. Он хочет работать не более 160 часов в месяц. У него 800 ромбов. Ниже дается прибыль, время труда и количество ромбов, необходимых для получения каждого товара. Если потребность в каждом продукте не ограничена, как Максим может увеличить прибыль?
Продукт
Прибыль за единицу
Трудоемкие часы на единицу
Ромбы на единицу
Лексема
300р.
.35
1,2
Кулигов
200 ₽
.15
.75
Кулигов
100р.
0,05
.5










