Acest articol descrie sintaxa de formulă și utilizarea funcției ZTEST în Microsoft Excel.
Returnează o valoare a probabilității unilaterale a testului z. Pentru o medie ipotetică dată a populației, μ0, ZTEST returnează probabilitatea ca media eșantionului să fie mai mare decât media observațiilor din setul de date (matrice) — adică, media observată a eșantionului.
Pentru a vedea cum poate fi utilizată funcția ZTEST într-o formulă pentru a calcula o valoare a probabilității bilaterale, consultați remarcile de mai jos.
Important: Această funcție a fost înlocuită cu una sau mai multe funcții noi care pot oferi precizie îmbunătățită și ale căror nume reflectă mai bine utilizarea lor. Deși această funcție este în continuare disponibile pentru compatibilitate retroactivă, se recomandă să luați în considerare utilizarea funcțiilor noi de acum înainte, deoarece este posibil ca această funcție să nu mai fie disponibilă în versiunile viitoare de Excel.
Pentru mai multe informații despre noua funcție, consultați Funcția Z.TEST.
Sintaxă
ZTEST(matrice,x,[sigma])
Sintaxa funcției ZTEST are următoarele argumente:
-
Matrice Obligatoriu. Este matricea sau zona de date față de care va fi testată valoarea x.
-
X Obligatoriu. Este valoarea de testat.
-
Sigma Opțional. Este abaterea standard a populației (cunoscută). Dacă este omisă, se folosește abaterea standard a eșantionului.
Observații
-
Dacă setul de date matrice este gol, ZTEST întoarce valoarea de eroare #N/A.
-
ZTEST este calculată după cum urmează, când sigma nu se omite:
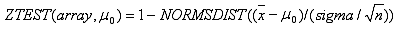
sau când sigma se omite:
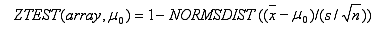
unde x este media eșantionului AVERAGE(matrice); s este abaterea standard a eșantionului STDEV(matrice); iar n este numărul de observații din eșantionul COUNT(matrice).
-
ZTEST reprezintă probabilitatea ca media eșantionului să fie mai mare decât valoarea observată AVERAGE(matrice), când media populației de bază este μ0. Din simetria repartiției normale, dacă AVERAGE(atrice) < μ0, ZTEST va returna o valoare mai mare decât 0,5.
-
Următoarea formulă Excel poate fi utilizată pentru a calcula probabilitatea bilaterală ca media eșantionului să fie mai depărtată de μ0 (în ambele direcții) decât de AVERAGE(matrice), când media populației de bază este μ0:
=2 * MIN(ZTEST(matrice;μ0;sigma); 1 - ZTEST(matrice;μ0;sigma)).
Exemplu
Copiați datele din exemplele din următorul tabel și lipiți-le în celula A1 a noii foi de lucru Excel. Pentru ca formulele să afișeze rezultate, selectați-le, apăsați pe F2, apoi pe Enter. Dacă trebuie, puteți ajusta lățimea coloanei pentru a vedea toate datele.
|
Date |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Formulă |
Descriere (Rezultat) |
Rezultat |
|
=ZTEST(A2:A11,4) |
Valoarea probabilității unilaterale a testului z pentru setul de date de mai sus, la media ipotetică a populației de 4 (0,090574) |
0,090574 |
|
=2 * MIN(ZTEST(A2:A11;4), 1 - ZTEST(A2:A11;4)) |
Valoarea probabilității bilaterale a testului z pentru setul de date de mai sus, la media ipotetică a populației de 4 (0,181148) |
0,181148 |
|
=ZTEST(A2:A11;6) |
Valoarea probabilității unilaterale a testului z pentru setul de date de mai sus, la media ipotetică a populației de 6 (0,863043) |
0,863043 |
|
=2 * MIN(ZTEST(A2:A11;6); 1 - ZTEST(A2:A11;6)) |
Valoarea probabilității bilaterale a testului z pentru setul de date de mai sus, la media ipotetică a populației de 6 (0,273913) |
0,273913 |










