Utilizar o Solver para orçamentação de capital

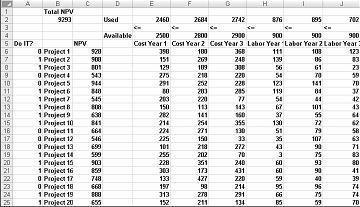
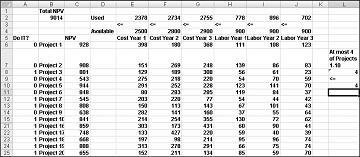
A maioria das empresas quer realizar projetos que contribuam com o maior valor líquido atual (VAL), sujeito a recursos limitados (normalmente capital e mão-de-obra). Digamos que uma empresa de desenvolvimento de software está a tentar determinar qual dos 20 projetos de software deve realizar. O VAL (em milhões de dólares) contribuiu para cada projeto, bem como para o capital (em milhões de dólares) e o número de programadores necessários durante cada um dos próximos três anos é dado na folha de cálculo Modelo Básico no ficheiro Capbudget.xlsx, que é apresentado na Figura 30-1 na página seguinte. Por exemplo, o Project 2 rende 908 milhões de dólares. Requer $151 milhões durante o Ano 1, $269 milhões durante o Ano 2, e $248 milhões durante o Ano 3. O Projecto 2 requer 139 programadores durante o Ano 1, 86 programadores durante o Ano 2 e 83 programadores durante o Ano 3. As células E4:G4 mostram o capital (em milhões de dólares) disponível durante cada um dos três anos e as células H4:J4 indicam quantos programadores estão disponíveis. Por exemplo, durante o Ano 1, estão disponíveis até 2,5 mil milhões de dólares em capital e 900 programadores.

A empresa tem de decidir se deve realizar cada projeto. Vamos supor que não podemos realizar uma fração de um projeto de software; se alocarmos 0,5 dos recursos necessários, por exemplo, teríamos um programa de não trabalho que nos traria 0 $ de receita!

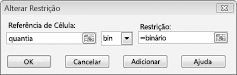
O truque em situações de modelação em que faz ou não faz algo é utilizar células de alteração binária. Uma célula de alteração binária é sempre igual a 0 ou 1. Quando uma célula binária que corresponde a um projeto é igual a 1, fazemos o projeto. Se uma célula binária que corresponde a um projeto for igual a 0, não fazemos o projeto. Configure o Solver para utilizar um intervalo de células de alteração binária ao adicionar uma restrição. Selecione as células que pretende utilizar e, em seguida, selecione Bin na lista na caixa de diálogo Adicionar Restrição.

Com este fundo, estamos prontos para resolver o problema de seleção do projeto de software. Como sempre com um modelo solver, começamos por identificar a nossa célula de destino, as células em mudança e as restrições.

• Célula de destino. Maximizamos o VAL gerado pelos projetos selecionados.

• Alterar células. Procuramos uma célula de alteração binária 0 ou 1 para cada projeto. Localizei estas células no intervalo A6:A25 (e dei o nome do doit ao intervalo). Por exemplo, um 1 na célula A6 indica que realizamos o Projeto 1; um 0 na célula C6 indica que não realizamos o Projeto 1.

• Restrições. Temos de garantir que, para cada Ano t (t=1, 2, 3), o ano em que o capital t é menor ou igual ao Ano em que o capital disponível está disponível, e a mão-de-obra year t utilizada é menor ou igual à mão-de-obra ano t disponível.

Como pode ver, a nossa folha de cálculo tem de calcular para qualquer seleção de projetos o VAL, o capital utilizado anualmente e os programadores utilizados todos os anos. Na célula B2, utilizo a fórmula SUMPRODUCT(doit,VAL) para calcular o total de VAL gerado por projetos selecionados. (O nome do intervalo VAL refere-se ao intervalo C6:C25.) Para cada projeto com um 1 na coluna A, esta fórmula escolhe o VAL do projeto e, para cada projeto com um 0 na coluna A, esta fórmula não recolhe o VAL do projeto. Portanto, somos capazes de calcular o VAL de todos os projetos e a nossa célula de destino é linear porque é calculada ao somar termos que seguem o formulário (alterar célula)*(constante). De forma semelhante, calculo o capital utilizado todos os anos e a mão-de-obra utilizada anualmente ao copiar de E2 para F2:J2 a fórmula SUMPRODUCT(doit;E6:E25).

Agora preenchi a caixa de diálogo Parâmetros do Solver, conforme mostrado na Figura 30-2.

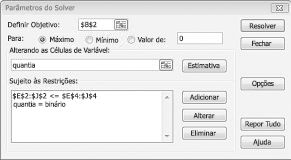
O nosso objetivo é maximizar o VAL dos projetos selecionados (célula B2). As nossas células alteradas (o intervalo com o nome doit) são as células de alteração binária para cada projeto. A restrição E2:J2<=E4:J4 garante que, durante cada ano, o capital e a mão-de-obra utilizados são menores ou iguais ao capital e à mão-de-obra disponíveis. Para adicionar a restrição que torna as células de alteração binárias, clico em Adicionar na caixa de diálogo Parâmetros do Solver e, em seguida, seleciono Bin na lista no meio da caixa de diálogo. A caixa de diálogo Adicionar Restrição deve aparecer conforme mostrado na Figura 30-3.

O nosso modelo é linear porque a célula de destino é calculada como a soma dos termos que têm o formulário (célula em alteração)*(constante) e porque as restrições de utilização de recursos são calculadas ao comparar a soma de (alterar células)*(constantes) com uma constante.

Com a caixa de diálogo Parâmetros do Solver preenchida, clique em Resolver e temos os resultados apresentados anteriormente na Figura 30-1. A empresa pode obter um VALOR VAL máximo de 9.293 milhões de dólares (9,293 mil milhões de dólares) ao selecionar Projetos 2, 3, 6-10, 14-16, 19 e 20.

Por vezes, os modelos de seleção de projetos têm outras restrições. Por exemplo, suponha que, se selecionarmos o Projeto 3, também temos de selecionar o Projeto 4. Uma vez que a nossa solução ideal atual seleciona o Project 3, mas não o Project 4, sabemos que a nossa solução atual não pode permanecer ideal. Para resolver este problema, basta adicionar a restrição de que a célula de alteração binária do Project 3 é menor ou igual à célula de alteração binária do Project 4.

Pode encontrar este exemplo na folha de cálculo Se 3 e 4 no ficheiro Capbudget.xlsx, que é apresentada na Figura 30-4. A célula L9 refere-se ao valor binário relacionado com o Project 3 e à célula L12 ao valor binário relacionado com o Project 4. Ao adicionar a restrição L9<=L12, se escolhermos Projeto 3, L9 é igual a 1 e a nossa restrição força L12 (o binário do Projeto 4) a ser igual a 1. A nossa restrição também tem de deixar o valor binário na célula de alteração do Project 4 sem restrições se não selecionarmos o Project 3. Se não selecionarmos o Projeto 3, L9 é igual a 0 e a nossa restrição permite que o binário do Project 4 seja igual a 0 ou 1, que é o que queremos. A nova solução ideal é apresentada na Figura 30-4.

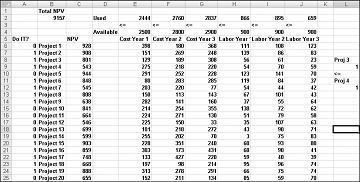
Uma nova solução ideal é calculada se selecionar o Project 3 significa que também temos de selecionar o Project 4. Agora, suponha que só podemos fazer quatro projetos entre os Projetos 1 e 10. (Consulte a folha de cálculo No Máximo 4 de P1–P10 , apresentada na Figura 30-5.) Na célula L8, calculamos a soma dos valores binários associados aos Projetos 1 a 10 com a fórmula SOMA(A6:A15). Em seguida, adicionamos a restrição L8<=L10, que garante que, no máximo, 4 dos primeiros 10 projetos estão selecionados. A nova solução ideal é apresentada na Figura 30-5. O VAL baixou para 9,014 biliões de dólares.

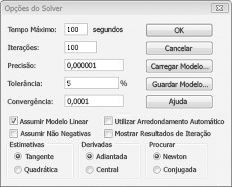
Os modelos lineares do Solver nos quais algumas ou todas as células em mudança têm de ser binárias ou números inteiros são normalmente mais difíceis de resolver do que os modelos lineares em que todas as células em mudança têm permissão para serem frações. Por este motivo, estamos muitas vezes satisfeitos com uma solução quase ideal para um problema de programação binária ou de número inteiro. Se o modelo solver for executado durante muito tempo, poderá considerar ajustar a definição Tolerância na caixa de diálogo Opções do Solver. (Consulte a Figura 30-6.) Por exemplo, uma definição de Tolerância de 0,5% significa que o Solver irá parar na primeira vez que encontrar uma solução viável que esteja dentro de 0,5% do valor teórico ideal da célula de destino (o valor teórico ideal da célula de destino é o valor de destino ideal encontrado quando as restrições binárias e de número inteiro são omitidas). Muitas vezes, somos confrontados com uma escolha entre encontrar uma resposta dentro de 10% do ideal em 10 minutos ou encontrar uma solução ideal em duas semanas de tempo do computador! O valor de Tolerância predefinido é 0,05%, o que significa que o Solver para quando encontra um valor de célula de Destino dentro de 0,05% do valor teórico ideal da célula de destino.

1. Uma empresa tem nove projetos em consideração. O VAL adicionado por cada projeto e o capital exigido por cada projeto durante os próximos dois anos é apresentado na tabela seguinte. (Todos os números estão em milhões.) Por exemplo, o Project 1 adicionará 14 milhões de dólares em VAL e exigirá despesas de 12 milhões de dólares durante o Ano 1 e 3 milhões durante o Ano 2. Durante o Ano 1, estão disponíveis 50 milhões de dólares em capital para projectos, e 20 milhões de dólares estão disponíveis durante o Ano 2.

	VAL	Despesas do ano 1	Despesas do ano 2
Projeto 1	14	12	3
Projeto 2	17	54	7
Projeto 3	17	6	6
Projeto 4	15	6	2
Projeto 5	40	30	35
Projeto 6	12	6	6
Projeto 7	14	48	4
Projeto 8	10	36	3
Project 9	12	18	3

• Se não conseguirmos realizar uma fração de um projeto, mas tivermos de realizar um projeto inteiro ou nenhum, como podemos maximizar o VAL?

• Suponha que, se o Project 4 for realizado, o Project 5 tem de ser realizado. Como podemos maximizar o VAL?

• Uma editora está a tentar determinar qual dos 36 livros deve publicar este ano. O ficheiro Pressdata.xlsx fornece as seguintes informações sobre cada livro:

  • Receita prevista e custos de desenvolvimento (em milhares de dólares)

  • Páginas em cada livro

  • Se o livro está orientado para uma audiência de programadores de software (indicado por um 1 na coluna E)

    Uma editora pode publicar livros num total de até 8500 páginas este ano e tem de publicar pelo menos quatro livros direcionados para programadores de software. Como pode a empresa maximizar os seus lucros?

Este artigo foi adaptado a partir da Análise de Dados e Modelação de Negócio do Microsoft Office Excel 2007 por Wayne L. Winston.

Este livro em estilo de sala de aula foi desenvolvido a partir de uma série de apresentações de Wayne Winston, um estatístico conhecido e professor de negócios especializado em aplicações criativas e práticas do Excel.