Nota: Queremos fornecer-lhe os conteúdos de ajuda mais recentes o mais rapidamente possível e no seu idioma. Esta página foi traduzida automaticamente e pode conter erros gramaticais ou imprecisões. O nosso objetivo é que estes conteúdos lhe sejam úteis. Pode informar-nos se as informações foram úteis no final desta página? Eis o artigo em inglês para referência.
Este artigo descreve como utilizar o Solver, um programa suplementar do Microsoft Excel que pode utilizar para a análise de hipóteses, para determinar uma combinação de produtos ideal.
Como posso determinar a combinação de produtos mensal que maximiza a lucratividade?
Muitas vezes, as empresas têm de determinar a quantidade de cada produto para serem produzidos mensalmente. De forma mais simples, o problema de combinação de produtos envolve como determinar a quantidade de cada produto que deve ser produzida durante um mês para maximizar os lucros. A combinação de produtos tem em geral obedecer às seguintes restrições:
-
A combinação de produtos não pode utilizar mais recursos do que o disponível.
-
Existe uma demanda limitada para cada produto. Não nos é possível produzir mais de um produto durante um mês do que a demanda de demandas, uma vez que o excesso de produção é desperdiçado (por exemplo, um medicamento perishable).
Vamos agora resolver o seguinte exemplo do problema de combinação de produtos. Pode encontrar a solução para este problema no ficheiro prodmix. xlsx, apresentado na Figura 27-1.
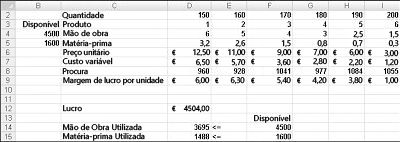
Vamos dizer que trabalhamos para uma empresa farmacêutica que produz seis produtos diferentes na sua fábrica. A produção de cada produto requer mão-de-obra e material bruto. A linha 4 na Figura 27-1 mostra as horas de trabalho necessárias para produzir uma libra de cada produto, sendo que a linha 5 mostra as libras de material bruto necessário para produzir uma libra de cada produto. Por exemplo, produzir uma libra do produto 1 requer seis horas de trabalho e 3,2 libras de matéria-prima. Para cada medicamento, o preço por libra é fornecido na linha 6, o custo unitário por libra é fornecido na linha 7 e a contribuição de lucro por libra é dada na linha 9. Por exemplo, as vende do produto 2 para o $11 por libra, incorrem um custo unitário de $5.70 por libra e contribui com o lucro de $5.30 por libra. A demanda do mês para cada medicamento é dada na linha 8. Por exemplo, a demanda para o produto 3 é de 1041 kg. Este mês, 4500 horas de trabalho e 1600 libras de matéria-prima estão disponíveis. De que forma esta empresa pode maximizar o seu lucro mensal?
Caso não saiba nada sobre o Solver do Excel, iremos atacar este problema ao criar uma folha de cálculo para monitorizar a utilização de lucros e recursos associada à combinação de produtos. Em seguida, iremos utilizar a versão de avaliação e o erro para variar a combinação de produtos para otimizar o lucro sem utilizar mais mão-de-obra ou material bruto do que o disponível e sem ter de produzir qualquer medicamento em excesso de demanda. Utilizamos o Solver neste processo apenas na fase de avaliação e de erros. Basicamente, o Solver é um motor de otimização que executa sem falhas a pesquisa de avaliação e de erros.
Uma chave para resolver o problema da combinação de produtos consiste em calcular eficientemente a utilização de recursos e a lucratividade associados a qualquer combinação de produtos específica. Uma ferramenta importante que podemos utilizar para fazer esta computação é a função SOMARPRODUTO. A função SOMARPRODUTO multiplica os valores correspondentes em intervalos de células e devolve a soma dos valores. Cada intervalo de células utilizado numa avaliação SOMARPRODUTO tem de ter as mesmas dimensões, o que significa que pode utilizar SOMARPRODUTO com duas linhas ou duas colunas, mas não com uma coluna e uma linha.
Como exemplo de como podemos utilizar a função SOMARPRODUTO no nosso exemplo de combinação de produtos, vamos tentar calcular a nossa utilização de recursos. A utilização da nossa mão de obra é calculada por
(Mão-de-obra utilizado por libra do medicamento 1) * (são produzidas as libras do medicamento 1) + (mão-de-obra utilizado por libra do medicamento 2) * (são produzidas por 2 quilos) +... (Mão-de-me utilizado por libra do medicamento 6) * (são produzidas 6 quilos)
Poderíamos calcular a utilização de mão-de-obra de forma mais entediante como D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + i2 * i4. Da mesma forma, a utilização de material bruto pode ser calculada como d2 * d5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + i2 * i5. No enTanto, a introdução destas fórmulas numa folha de cálculo para seis produtos é demorada. Imagine quanto tempo poderia decorrer se estivesse a trabalhar com uma empresa que produziu, por exemplo, produtos do 50 na sua fábrica. Uma forma muito mais fácil de calcular mão-de-obra e utilização de materiais brutos é copiar do D14 para D15 a fórmula SOMARPRODUTO ($D $2: $I $2, D4: i4). Esta fórmula computa o D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + i2 * i4 (que é a nossa utilização de trabalho), mas é muito mais fácil de entrar! RePare que utilizo o sinal $ com o intervalo D2: i2 de forma a que, quando copiar a fórmula, ainda Capture a combinação de produtos da linha 2. A fórmula na célula D15 computa a utilização de matéria-prima.
De forma semelhante, o nosso lucro é determinado por
(Lucro do medicamento 1 por libra) * (são produzidas as libras do medicamento 1) + (lucro do medicamento 2 por libra) * (libras do medicamento 2 produzidas) +... (Lucro do medicamento 6 por libra) * (libras do medicamento 6 produzidas)
O lucro é facilmente calculado na célula D12 com a fórmula SOMARPRODUTO (D9: i9, $D $2: $I $2).
Agora podemos identificar os três componentes do nosso modelo do Solver de produtos.
-
Célula de destino.O nosso objetivo é maximizar o lucro (calculado na célula D12).
-
Alterar células.O número de libras produzidas de cada produto (listado no intervalo de células D2: i2)
-
Alguma. Temos as seguintes restrições:
-
Não utilizem mais mão-de-obra ou material bruto do que o disponível. Ou seja, os valores nas células D14: D15 (os recursos utilizados) têm de ser menores ou iguais aos valores nas células F14: F15 (os recursos disponíveis).
-
Não produza mais de um medicamento do que há em demanda. Ou seja, os valores nas células D2: i2 (libras produzidas por cada medicamento) devem ser menores ou iguais à demanda de cada medicamento (listado nas células D8: i8).
-
Não é possível produzir um montante negativo de qualquer medicamento.
-
Vou mostrar-lhe como introduzir a célula de destino, alterar as células e as restrições para o Solver. Em seguida, basta clicar no botão resolver para encontrar uma combinação de produtos que maximize o lucro!
Para começar, clique no separador dados e, no grupo análise, clique em Solver.
Nota: Conforme explicado no capítulo 26, "introdução à otimização com o Excel Solver", o Solver está instalado ao clicar no botão do Microsoft Office e, em seguida, em opções do Excel, seguido de suplementos. Na lista gerir, clique em suplementos do Excel, selecione a caixa suplementar do Solver e, em seguida, clique em OK.
Será apresentada a caixa de diálogo parâmetros do Solver, conforme apresentado na Figura 27-2.
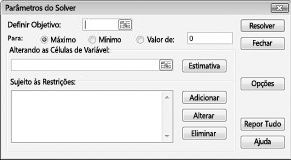
Clique na caixa definir célula de destino e, em seguida, selecione a nossa célula de lucro (célula D12). Clique na caixa ao alterar as células e, em seguida, aponte para o intervalo D2: i2, que contém as libras produzidas de cada medicamento. A caixa de diálogo deverá ter agora a Figura 27-3.
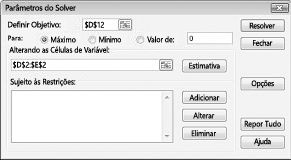
Agora estamos prontos para adicionar restrições ao modelo. Clique no botão Adicionar. Irá ver a caixa de diálogo Adicionar restrição, apresentada na Figura 27-4.
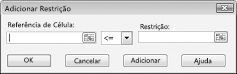
Para adicionar as restrições de utilização de recursos, clique na caixa referência de célula e, em seguida, selecione o intervalo D14: D15. Selecione < = na lista do meio. Clique na caixa de restrição e, em seguida, selecione o intervalo de células F14: F15. A caixa de diálogo Adicionar restrição deverá agora parecer com a imagem 27-5.
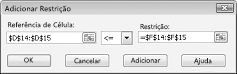
Garantimos que, quando o Solver tentar valores diferentes para as células variáveis, apenas as combinações que satisfaçam D14< = F14 (trabalho utilizado é menor ou igual a mão-de-obra disponível) e D15< = F15 (o material bruto utilizado é menor ou igual a material bruto disponível) será considerado. Clique em Adicionar para introduzir as restrições de demanda. Preencha a caixa de diálogo Adicionar restrição, conforme apresentado na Figura 27-6.
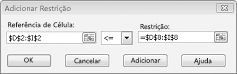
Adicionar estas restrições assegura que, quando o Solver tentar combinações diferentes para os valores de células variáveis, serão consideradas apenas combinações que satisfaçam os seguintes parâmetros:
-
D2< = D8 (a quantidade produzida do medicamento 1 é menor ou igual à demanda do medicamento 1)
-
E2< = E8 (a quantidade de produção do medicamento 2 é menor ou igual à demanda do medicamento 2)
-
F2< = F8 (a quantidade produzida do medicamento 3 produzida é menor ou igual à demanda do medicamento 3)
-
G2< = G8 (a quantidade produzida do medicamento 4 produzida é menor ou igual à demanda do medicamento 4)
-
H2< = H8 (a quantidade produzida do medicamento 5 produzida é menor ou igual à demanda do medicamento 5)
-
I2< = i8 (a quantidade produzida do medicamento 6 é menor ou igual à demanda do medicamento 6)
Clique em OK na caixa de diálogo Adicionar restrição. A janela do Solver deverá ter o seguinte aspecto na imagem 27-7.
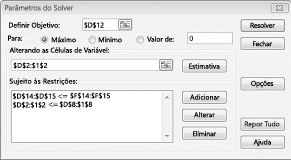
Introduzimos a restrição que a alteração de células tem de ser não negativo na caixa de diálogo opções do Solver. Clique no botão Opções na caixa de diálogo parâmetros do Solver. Selecione a caixa assumir modelo linear e a caixa assumir não negativo, conforme apresentado na Figura 27-8 na página seguinte. Clique em OK.
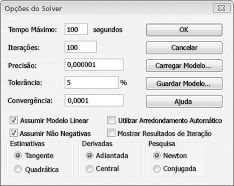
Marcar a caixa pressupor que não é negativo garante que o Solver só considera combinações de células variáveis em que cada célula de alteração assuma um valor não negativo. Assinalei a caixa assumir modelo linear porque o problema de combinação de produtos é um tipo especial de problema do Solver denominado modelo linear. Basicamente, um modelo do Solver é linear sob as seguintes condições:
-
A célula de destino é calculada ao somar as condições do formulário (célula variável) * (constante).
-
Cada restrição cumpre o "requisito de modelo linear". Isto significa que cada restrição é avaliada ao adicionar os termos do formulário (célula variável) * (constante) e comparar as somas com uma constante.
Por que motivo é que o problema do Solver é linear? A nossa célula de destino (lucro) é calculada como
(Lucro do medicamento 1 por libra) * (são produzidas as libras do medicamento 1) + (lucro do medicamento 2 por libra) * (libras do medicamento 2 produzidas) +... (Lucro do medicamento 6 por libra) * (libras do medicamento 6 produzidas)
Esta computação segue um padrão no qual o valor da célula de destino é derivado ao somar os termos do formulário (célula variável) * (constante).
A nossa restrição de mão-de-obra é avaliada pela comparação do valor derivado de (mão-de-obra utilizada por libra do medicamento 1) * (farmácia 1 libras produzidas) + (mão-de-obra utilizado por tralha de 2) * (medicamento 2 libras produzidas) +... (Mão-de- me Ed por libra do medicamento 6) * (são produzidas no medicamento 6 libras) para o trabalho disponível.
Por conSeguinte, a restrição de mão-de-obra é avaliada ao adicionar os termos do formulário (célula variável) * (constante) e comparar as somas com uma constante. A restrição de mão-de-obra e a restrição de material bruto satisfazem o requisito de modelo linear.
As nossas restrições de demanda têm a forma
(Medicamento 1 produzida) < = (demanda de medicamento 1) (medicamento 2 produzida) < = (Demand 2 Demand) § (medicamento 6 produzidos) < = (demanda do medicamento 6)
Cada restrição de demanda também cumpre o requisito de modelo linear, uma vez que cada uma delas é avaliada ao somar as condições do formulário (célula variável) * (constante) e comparar as somas a uma constante.
Tendo mostrado que o nosso modelo de combinação de produtos é um modelo linear, por que motivo devo ter em atenção?
-
Se um modelo do Solver for linear e selecionar assumir modelo linear, a resolução do Solver será garantida para encontrar a solução ideal para o modelo do Solver. Se um modelo do Solver não for linear, o Solver poderá ou não encontrar a solução ideal.
-
Se um modelo do Solver for linear e selecionar assumir modelo linear, o Solver utiliza um algoritmo muito eficiente (o método simplex) para encontrar a solução ideal do modelo. Se um modelo do Solver for linear e não selecionar assumir modelo linear, o Solver utilizará um algoritmo muito ineficiente (o método GRG2) e poderá ter dificuldades em encontrar a solução ideal do modelo.
Depois de clicar em OK na caixa de diálogo opções do Solver, voltamos à caixa de diálogo principal do Solver, apresentada anteriormente na Figura 27-7. Ao clicar em resolução, o Solver calcula uma solução ideal (caso exista uma) para o nosso modelo de combinação de produtos. Como declarei no capítulo 26, uma solução ideal para o modelo de combinação de produtos seria um conjunto de valores de células de alteração (libras produzidas de cada medicamento) que maximizam o lucro sobre o conjunto de todas as soluções viáveis. Mais uma vez, uma solução viável é um conjunto de valores de células variáveis que satisfaçam todas as restrições. Os valores de células variáveis apresentados na Figura 27-9 são uma solução viável, uma vez que todos os níveis de produção são não negativos, os níveis de produção não ultrapassam a demanda e a utilização de recursos não ultrapassa os recursos disponíveis.
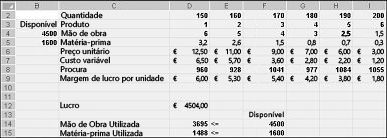
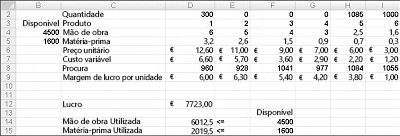
Os valores das células em mudança apresentados na Figura 27-10 na página seguinte representam uma solução inviável pelos seguintes motivos:
-
Geramos mais do medicamento 5 do que a demanda por ela.
-
Utilizamos mais mão-de-obra do que a que está disponível.
-
Utilizamos um material mais bruto do que o disponível.
Depois de clicar em resolução, o Solver encontra rapidamente a solução ideal apresentada na Figura 27-11. Tem de selecionar manter solução do Solver para preservar os valores de solução ideais na folha de cálculo.
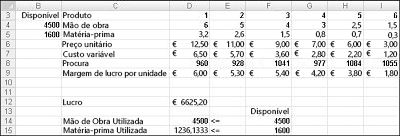
A nossa empresa farmacêutica pode maximizar o seu lucro mensal num nível de $6625.20 ao produzir 596,67 libras do medicamento 4, 1084 libras do medicamento 5 e nenhum dos outros medicamentos! Não nos é possível determinar se podemos obter o lucro máximo de $6625.20 de outras formas. Só temos a certeza de que, com os nossos recursos e demandas limitados, não é possível disponibilizar mais do que $6627.20 este mês.
SuPonhamos que a demanda para cada produto tem de ser cumprida. (Consulte a folha de cálculo nenhuma solução viável no ficheiro prodmix. xlsx.) Em seguida, temos de alterar as nossas restrições de demanda de D2: I2< = D8: i8 para D2: I2> = D8: i8. Para o fazer, abra o Solver, selecione a restrição D2: I2< = D8: i8 e, em seguida, clique em alterar. É apresentada a caixa de diálogo Alterar restrição, apresentada na Figura 27-12.
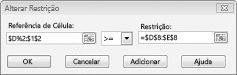
Selecione > = e, em seguida, clique em OK. Garantimos que o Solver irá considerar a alteração apenas dos valores das células que cumprem todas as demandas. Quando clicar em resolver, verá a mensagem "o Solver não conseguiu encontrar uma solução viável". Esta mensagem não significa que cometemos um erro no nosso modelo, mas, em vez disso, com os nossos recursos limitados, não nos é possível cumprir as demandas de todos os produtos. O Solver está a apenas informar que, se quisermos cumprir as demandas de cada produto, precisamos de adicionar mais mão-de-obra, mais materiais brutos ou de ambos.
Vejamos o que acontece se permitisse uma demanda ilimitada para cada produto e permitimos que sejam produzidas quantidades negativas de cada medicamento. (Pode ver este problema do Solver na folha de cálculo definir valores não convergir no ficheiro prodmix. xlsx.) Para encontrar a solução ideal para esta situação, abra o Solver, clique no botão Opções e, em seguida, desmarque a caixa pressupor não negativo. Na caixa de diálogo parâmetros do Solver, selecione a restrição de demanda D2: I2< = D8: i8 e, em seguida, clique em eliminar para remover a restrição. Ao clicar em resolver, o Solver devolve a mensagem "definir valores de célula não convergir". Esta mensagem significa que, se a célula de destino for maximizada (como no nosso exemplo), existem soluções viáveis com valores de células de destino arbitrariamente grandes. (Se a célula de destino for minimizada, a mensagem "definir valores de célula não conver" significa que existem soluções viáveis com valores de células de destino arbitrariamente pequenos.) Na nossa situação, ao permitir a produção negativa de um medicamento, estamos em vigor "criar" recursos que podem ser utilizados para produzir quantidades arbitrárias de outros medicamentos. Devido à nossa demanda ilimitada, isto permite-nos efectuar-nos lucros ilimitados. Numa situação real, não podemos tornar um montante infinito de dinheiro. Resumindo, se vir "definir valores não convergir", o seu modelo tem um erro.
-
SuPonhamos que a nossa empresa farmacêutica possa comprar até 500 horas de trabalho em $1 mais por hora do que os custos de mão-de-obra atuais. Como posso maximizar o lucro?
-
Numa fábrica de manufatura de chips, quatro técnicos (A, B, C e D) produzem três produtos (produtos 1, 2 e 3). Este mês, o fabricante do chip pode vender unidades de 80 do produto 1, 50 unidades de produto 2 e na maioria das unidades do 50 do produto 3. O técnico A só pode fazer os produtos 1 e 3. O técnico B só pode fazer os produtos 1 e 2. O técnico C só pode fazer o produto 3. O técnico D só pode fazer o produto 2. Para cada unidade produzida, os produtos contribuem o seguinte lucro: produto 1, $6; Produto 2, $7; e o produto 3, $10. O tempo (em horas) em que cada técnico tem de fabricar um produto é o seguinte:
Produto
Técnico A
Técnico B
Técnico C
Técnico D
1
2
2,5
Não é possível fazer
Não é possível fazer
2
Não é possível fazer
3
Não é possível fazer
3,5
3
3
Não é possível fazer
4
Não é possível fazer
-
Cada técnico pode trabalhar até 120 horas por mês. Como é que o fabricante do chip pode maximizar o seu lucro mensal? Presuma que é possível produzir um número fracionário de unidades.
-
Uma fábrica de fabricação de computadores produz um mouse, teclados e joysticks de videogames. O lucro por unidade, a utilização do trabalho por unidade, a demanda mensal e a utilização por tempo da máquina por unidade são apresentadas na seguinte tabela:
Mouse
Teclados
Joysticks
Lucro/unidade
$8
$11
$9
Utilização/unidade de trabalho de mão
.2 horas
.3 horas
.24 horas
Hora/unidade do computador
.04 horas
.055 hora
.04 horas
Demanda mensal
15.000
27.000
11.000
-
Todos os meses, um total de 13.000 horas de trabalho e 3000 horas de tempo de máquina estão disponíveis. Como é que o fabricante pode maximizar a sua contribuição de lucro mensal da fábrica?
-
Resolva o nosso exemplo de medicamento pressupondo que é necessário cumprir uma demanda mínima de 200 unidades para cada medicamento.
-
Jason faz com que o Diamond Bracelets, Necklaces e Earrings. O mesmo pretende trabalhar no máximo de 160 horas por mês. Ele tem 800 onças de ouros. O lucro, o tempo de trabalho e as onças de ouros necessários para produzir cada produto são apresentados abaixo. Se a demanda para cada produto for ilimitada, como é que o Jason pode maximizar o seu lucro?
Produto
Lucro unitário
Horas de trabalho por unidade
Onças de ouros por unidade
Bracelet
€ 300
.35
1.2
Necklace
€ 200
.15
.75
Earrings
€ 100
0,05
0,5










