Este artigo descreve a sintaxe da fórmula e a utilização da função TESTEZ no Microsoft Excel.
Devolve o valor de probabilidade uni-caudal de um teste-z. Para uma determinada média da população hipotética, μ0, TESTEZ devolve a probabilidade de que a média da amostra seria maior do que a média de observações no conjunto de dados (matriz), ou seja, a média da amostra observada.
Para ver como TESTEZ pode ser utilizado numa fórmula para calcular um valor de probabilidade bi-caudal, consulte "Observações" abaixo.
Importante: Esta função foi substituída por uma ou mais novas funções que podem fornecer uma maior exatidão e cujos nomes refletem melhor a respetiva utilização. Embora esta função ainda esteja disponível para retrocompatibilidade, deve considerar a utilização das novas funções a partir de agora pois a mesma pode não estar disponível em versões futuras do Excel.
Para obter mais informações sobre a nova função, consulte a Função TESTE.Z.
Sintaxe
TESTEZ(matriz;x;[sigma])
A sintaxe da função TESTEZ tem os seguintes argumentos.
-
Matriz obrigatório. É a matriz ou intervalo de dados em que x será testado.
-
X obrigatório. É o valor que pretende testar.
-
Sigma opcional. É o desvio-padrão da população (conhecido). Se omitido, será utilizado o desvio-padrão do exemplos.
Observações
-
Se matriz estiver em branco, TESTEZ devolve o valor de erro #N/D.
-
TESTEZ é calculado da seguinte forma quando sigma não é omitido:
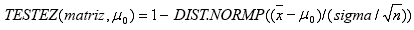
ou quando sigma é omitido:
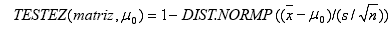
onde x é a MÉDIA(matriz) média da amostra; s é o DESVPAD(matriz) do desvio padrão da amostra; e n é o número de observações em CONTAR(matriz) da amostra.
-
TESTEZ representa a probabilidade de a média da amostra ser maior do que o valor observado em MÉDIA(matriz), quando a média da população subjacente for µ0. Da simetria da distribuição normal, se MÉDIA(matriz) < µ0, TESTEZ irá devolver um valor maior do que 0,5.
-
A seguinte fórmula do Excel pode ser utilizada para calcular a probabilidade bi-caudal de que a média da amostra estaria mais afastada de µ0 (em qualquer direção) do que a MÉDIA(matriz), quando a média da população subjacente for µ0:
=2 * MÍNIMO(TESTEZ(matriz,µ0,sigma), 1 - TESTEZ(matriz,µ0,sigma)).
Exemplo
Copie os dados de exemplo na tabela seguinte e cole-os na célula A1 de uma nova folha de cálculo do Excel. Para que as fórmulas mostrem resultados, selecione-as, prima F2 e, em seguida, prima Enter. Se pretender, pode ajustar as larguras das colunas para ver todos os dados.
|
Dados |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Fórmula |
Descrição (Resultado) |
Resultado |
|
=TESTEZ(A2:A11,4) |
Valor de probabilidade uni-caudal de um teste-z para o conjunto de dados acima, na média da população hipotética de 4 (0,090574) |
0,090574 |
|
=2 * MÍNIMO(TESTEZ(A2:A11,4), 1 - TESTEZ(A2:A11,4)) |
Valor de probabilidade bi-caudal de um teste-z para o conjunto de dados acima, na média da população hipotética de 4 (0,181148) |
0,181148 |
|
=TESTEZ(A2:A11,6) |
Valor de probabilidade uni-caudal de um teste-z para o conjunto de dados acima, na média da população hipotética de 6 (0,863043) |
0,863043 |
|
=2 * MÍNIMO(TESTEZ(A2:A11,6), 1 - TESTEZ(A2:A11,6)) |
Valor de probabilidade bi-caudal de um teste-z para o conjunto de dados acima, na média da população hipotética de 6 (0,273913) |
0,273913 |










