Este tópico aborda as diferentes opções de linha de tendência disponíveis no Office.
Utilize este tipo de linha de tendência linear para criar a linha reta que melhor se adapta a conjuntos de dados lineares simples. Os dados são lineares se o padrão nos respetivos pontos de dados se parecer a uma linha. Uma linha de tendência linear mostra, normalmente, que algo está a aumentar ou a diminuir num ritmo estável.
Uma linha de tendência utiliza esta equação para calcular o ajuste dos quadrados mínimos para uma linha:
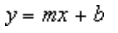
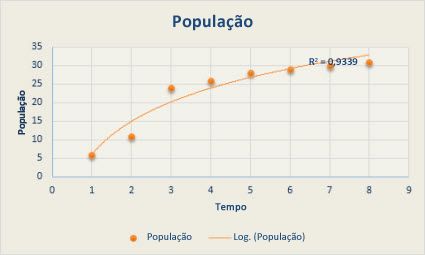
em que m representa o declive e b a interceção.
A linha de tendência linear seguinte mostra que as vendas de frigoríficos aumentaram de forma consistente ao longo de um período de 8 anos. Note que o valor de R ao quadrado (um número de 0 a 1 que revele até que ponto os valores estimados da linha de tendência correspondem aos dados reais) é 0,9792, o que representa uma boa adequação da linha aos dados.
Mostrando a linha curva que melhor se adapta, esta linha de tendência é útil quando a percentagem de alteração dos dados aumenta e diminui rapidamente e, em seguida, estabiliza. Uma linha de tendência logarítmica pode utilizar valores negativos e positivos.
Uma linha de tendência logarítmica utiliza esta equação para calcular o ajuste dos quadrados mínimos através de pontos:
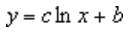
em que c e b são constantes e ln corresponde à função logarítmica natural.
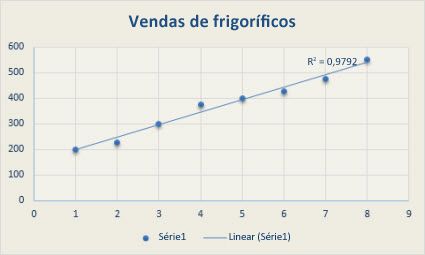
A linha de tendência logarítmica seguinte mostra o crescimento previsto da população animal numa área definida, onde o espaço disponível para os animais diminuiu, enquanto a população estabilizou. Note que o valor de R ao quadrado é 0,933, o que corresponde a um ajuste relativamente bom da linha aos dados.
Esta linha de tendência é útil quando os seus dados flutuam. Por exemplo, quando analisa ganhos e perdas num grande conjunto de dados. A ordem do polinomial pode ser determinada pelo número de flutuações nos dados ou pela quantidade de curvas (colinas e vales) que aparecem na curva. Normalmente, uma linha de tendência polinomial da Ordem 2 tem apenas uma colina ou vale, uma Ordem 3 tem uma ou duas colinas ou vales, e uma Ordem 4 tem até três colinas ou vales.
Uma linha de tendência polinominal ou curvilinear utiliza esta equação para calcular o ajuste dos quadrados mínimos através de pontos:
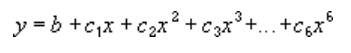
em que b e 
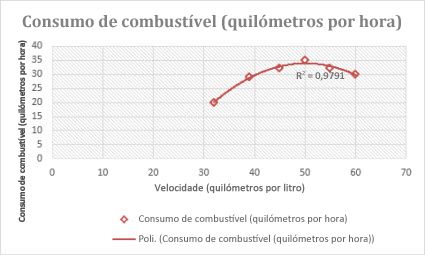
A linha de tendência polinomial número 2 (um máximo) seguinte mostra a relação entre a velocidade de condução e o consumo de combustível. Note que o valor de R ao quadrado é 0,979, o que está próximo de 1, correspondendo a um bom ajuste da linha aos dados.
Ao mostrar uma linha curva, esta linha de tendência é útil para conjuntos de dados que comparam medidas que aumentam a uma taxa específica. Por exemplo, a aceleração de um carro de corrida em intervalos de um segundo. Não é possível criar uma linha de tendência de potência se os dados apresentarem o valor 0 ou valores negativos.
Uma linha de tendência de potência utiliza esta equação para calcular o ajuste dos quadrados mínimos através de pontos:
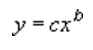
em que c e b são constantes.
Nota: Esta opção não está disponível quando os dados incluem valores de zero ou negativos.
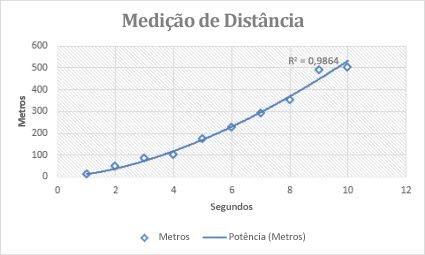
O gráfico de medida de distâncias mostra as distâncias em metros por segundo. A linha de tendência de potência mostra de forma clara o aumento da aceleração. Note que o valor de R ao quadrado é 0,986, o que corresponde a um ajuste quase perfeito da linha aos dados.
Mostrando uma linha curva, esta linha de tendência é útil quando os valores de dados aumentam ou diminuem em percentagens cada vez mais elevadas. Não é possível criar uma linha de tendência exponencial se os dados incluírem zero ou valores negativos.
Uma linha de tendência exponencial utiliza esta equação para calcular o ajuste dos quadrados mínimos através de pontos:
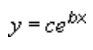
em que c e b são constantes e e corresponde à base do logaritmo natural.
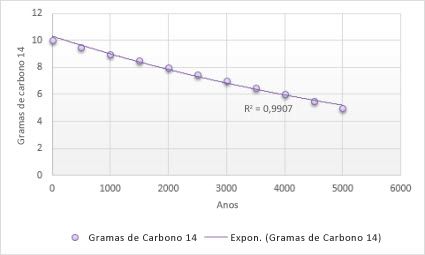
A linha de tendência exponencial mostra a diminuição do teor de carbono 14 à medida que um objeto envelhece. Note que o valor de R ao quadrado é 0,990, o que significa que a linha se ajusta quase perfeitamente aos dados.
Esta linha de tendência vai equilibrar as flutuações dos dados, de modo a mostrar um padrão ou uma tendência com maior clareza. Uma média móvel utiliza um número específico de pontos de dados (definido pela opção Período), calcula a respetiva média e utiliza o valor da média como um ponto na linha. Por exemplo, se o Período estiver definido como 2, a média dos dois primeiros pontos de dados é utilizada como primeiro ponto da linha de tendência de média móvel. A média do segundo e terceiro pontos de dados é utilizada como o segundo ponto da linha de tendência, e assim sucessivamente.
Uma linha de tendência de média móvel utiliza esta equação:
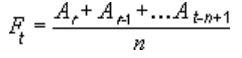
O número de pontos numa linha de tendência de média móvel é igual ao número total de pontos da série, menos o número especificado para o período.
Num gráfico de dispersão, a linha de tendência é baseada na ordem dos valores x no gráfico. Para obter melhores resultados, ordene os valores x antes de adicionar uma média móvel.
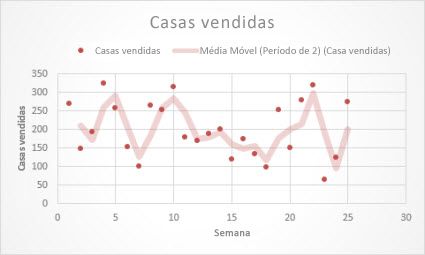
A linha de tendência de média móvel seguinte mostra um padrão no número de vendas de casas durante um período de 26 semanas.
Importante: A partir da versão 2005 do Excel, o Excel ajustou a forma como calcula o valor R2 para linhas de tendência lineares em gráficos em que a interceção da linha de tendência está definida como zero (0). Este ajuste corrige os cálculos que produziram valores R2 incorretos e alinha o cálculo R2 com a função PROJ.LIN. Como resultado, poderá ver diferentes valores R2 apresentados em gráficos criados anteriormente em versões anteriores do Excel. Para obter mais informações, veja Alterações aos cálculos internos das linhas de tendência lineares num gráfico.
Precisa de mais ajuda?
Pode sempre colocar uma pergunta a um especialista da Comunidade Tecnológica do Excel ou obter suporte nas Comunidades.
Consulte Também
Adicionar uma linha de média móvel ou de tendência a um gráfico










