Usando o Solver para orçamento de capital

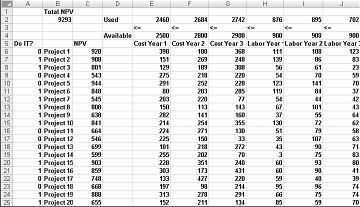
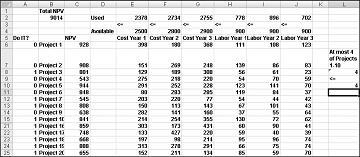
A maioria das corporações deseja realizar projetos que contribuam com o maior valor presente líquido (NPV), sujeitos a recursos limitados (geralmente capital e mão de obra). Digamos que uma empresa de desenvolvimento de software esteja tentando determinar qual dos 20 projetos de software deve ser realizado. O NPV (em milhões de dólares) contribuído por cada projeto, bem como o capital (em milhões de dólares) e o número de programadores necessários durante cada um dos próximos três anos é dado na planilha Modelo Básico no arquivo Capbudget.xlsx, que é mostrado na Figura 30-1 na próxima página. Por exemplo, o Project 2 rende US$ 908 milhões. Requer US$ 151 milhões durante o ano 1, US$ 269 milhões durante o ano 2 e US$ 248 milhões durante o ano 3. O Projeto 2 requer 139 programadores durante o ano 1, 86 programadores durante o ano 2 e 83 programadores durante o ano 3. As células E4:G4 mostram o capital (em milhões de dólares) disponível durante cada um dos três anos, e as células H4:J4 indicam quantos programadores estão disponíveis. Por exemplo, durante o ano 1 até US $ 2,5 bilhões em capital e 900 programadores estão disponíveis.

A empresa deve decidir se deve realizar cada projeto. Vamos supor que não podemos realizar uma fração de um projeto de software; se alocarmos 0,5 dos recursos necessários, por exemplo, teríamos um programa que não trabalhasse que nos traria uma receita de US$ 0!

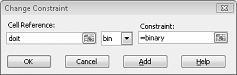
O truque em situações de modelagem em que você faz ou não faz algo é usar células de alteração binária. Uma célula de alteração binária sempre é igual a 0 ou 1. Quando uma célula de alteração binária que corresponde a um projeto é igual a 1, fazemos o projeto. Se uma célula de alteração binária que corresponde a um projeto for igual a 0, não faremos o projeto. Você configurou o Solver para usar um intervalo de células de alteração binária adicionando uma restrição: selecione as células de alteração que você deseja usar e escolha Bin na lista na caixa de diálogo Adicionar Restrição.

Com esse plano de fundo, estamos prontos para resolver o problema de seleção do projeto de software. Como sempre com um modelo solver, começamos identificando nossa célula de destino, as células em mudança e as restrições.

• Célula de destino. Maximizamos o NPV gerado por projetos selecionados.

• Alterando células. Procuramos uma célula de alteração binária de 0 ou 1 para cada projeto. Localizei essas células no intervalo A6:A25 (e nomeei o ponto de intervalo). Por exemplo, um 1 na célula A6 indica que realizamos o Projeto 1; um 0 na célula C6 indica que não realizamos o Projeto 1.

• Restrições. Precisamos garantir que para cada ano t (t=1, 2, 3), o capital t do ano usado seja menor ou igual ao ano t capital disponível, e o trabalho de ano t usado é menor ou igual ao ano t trabalho disponível.

Como você pode ver, nossa planilha deve computar para qualquer seleção de projetos o NPV, o capital usado anualmente e os programadores usados a cada ano. Na célula B2, uso a fórmula SUMPRODUCT(doit,NPV) para calcular o NPV total gerado por projetos selecionados. (O nome de intervalo NPV refere-se ao intervalo C6:C25.) Para cada projeto com um 1 na coluna A, essa fórmula capta o NPV do projeto e, para cada projeto com um 0 na coluna A, essa fórmula não capta o NPV do projeto. Portanto, somos capazes de calcular o NPV de todos os projetos e nossa célula de destino é linear porque ela é calculada resumindo os termos que seguem o formulário (alterando célula)*(constante). De forma semelhante, computo o capital usado a cada ano e o trabalho usado todos os anos copiando de E2 para F2:J2 a fórmula SUMPRODUCT(doit,E6:E25).

Agora preencha a caixa de diálogo Parâmetros do Solucionador, conforme mostrado na Figura 30-2.

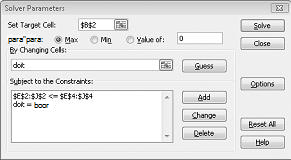
Nosso objetivo é maximizar o NPV de projetos selecionados (célula B2). Nossas células em alteração (o intervalo chamado doit) são as células de alteração binária para cada projeto. A restrição E2:J2<=E4:J4 garante que, durante cada ano, o capital e a mão-de-obra usados sejam menores ou iguais ao capital e ao trabalho disponíveis. Para adicionar a restrição que torna as células em alteração binárias, cliquei em Adicionar na caixa de diálogo Parâmetros do Solucionador e selecione Bin na lista no meio da caixa de diálogo. A caixa de diálogo Adicionar Restrição deve ser exibida conforme mostrado na Figura 30-3.

Nosso modelo é linear porque a célula de destino é calculada como a soma de termos que têm a forma (alteração de célula)*(constante) e porque as restrições de uso do recurso são calculadas comparando a soma de (alteração de células)*(constantes) a uma constante.

Com a caixa de diálogo Parâmetros do Solucionador preenchida, clique em Resolver e temos os resultados mostrados anteriormente na Figura 30-1. A empresa pode obter um NPV máximo de US$ 9.293 milhões (US$ 9,293 bilhões) escolhendo Projetos 2, 3, 6-10, 14-16, 19 e 20.

Às vezes, modelos de seleção de projeto têm outras restrições. Por exemplo, suponha que, se selecionarmos o Projeto 3, também devemos selecionar o Projeto 4. Como nossa solução ideal atual seleciona o Project 3, mas não o Project 4, sabemos que nossa solução atual não pode permanecer ideal. Para resolver esse problema, basta adicionar a restrição de que a célula de alteração binária do Project 3 seja menor ou igual à célula de alteração binária do Project 4.

Você pode encontrar este exemplo na planilha If 3 e 4 no arquivo Capbudget.xlsx, que é mostrado na Figura 30-4. A célula L9 refere-se ao valor binário relacionado ao Project 3 e à célula L12 ao valor binário relacionado ao Projeto 4. Ao adicionar a restrição L9<=L12, se escolhermos o Projeto 3, l9 será igual a 1 e nossa restrição força L12 (o binário do Project 4) a igual a 1. Nossa restrição também deve deixar o valor binário na célula de alteração do Project 4 irrestrita se não selecionarmos o Projeto 3. Se não selecionarmos o Projeto 3, l9 será igual a 0 e nossa restrição permitirá que o binário do Project 4 seja igual a 0 ou 1, que é o que queremos. A nova solução ideal é mostrada na Figura 30-4.

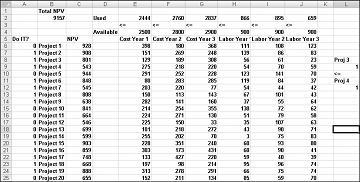
Uma nova solução ideal será calculada se selecionar o Projeto 3 significa que também devemos selecionar o Projeto 4. Agora suponha que possamos fazer apenas quatro projetos entre os Projetos 1 a 10. (Confira a planilha No máximo 4 de P1-P10 , mostrada na Figura 30-5.) Na célula L8, calculamos a soma dos valores binários associados aos Projetos 1 a 10 com a fórmula SUM(A6:A15). Em seguida, adicionamos a restrição L8<=L10, que garante que, no máximo, 4 dos primeiros 10 projetos sejam selecionados. A nova solução ideal é mostrada na Figura 30-5. O NPV caiu para US$ 9,014 bilhões.

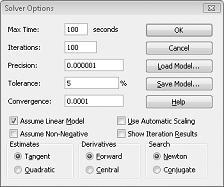
Modelos lineares do Solver nos quais algumas ou todas as células em mudança são necessárias para serem binárias ou inteiros geralmente são mais difíceis de resolver do que modelos lineares nos quais todas as células em mudança podem ser frações. Por esse motivo, muitas vezes estamos satisfeitos com uma solução quase ideal para um problema de programação binário ou inteiro. Se o modelo solver for executado por muito tempo, talvez você queira considerar ajustar a configuração tolerância na caixa de diálogo Opções do Solucionador. (Consulte Figura 30-6.) Por exemplo, uma configuração de tolerância de 0,5% significa que o Solver interromperá na primeira vez que encontrar uma solução viável que esteja dentro de 0,5% do valor teórico ideal da célula de destino (o valor teórico ideal da célula de destino é o valor ideal de destino encontrado quando as restrições binárias e inteiros são omitidas). Muitas vezes, nos deparamos com uma escolha entre encontrar uma resposta dentro de 10% do ideal em 10 minutos ou encontrar uma solução ideal em duas semanas de tempo de computador! O valor de tolerância padrão é 0,05%, o que significa que o Solver para quando encontra um valor de célula Target dentro de 0,05% do valor de célula de destino ideal teórico.

1. Uma empresa tem nove projetos em consideração. O NPV adicionado por cada projeto e o capital exigido por cada projeto durante os próximos dois anos é mostrado na tabela a seguir. (Todos os números estão em milhões.) Por exemplo, o Project 1 adicionará US$ 14 milhões em NPV e exigirá despesas de US$ 12 milhões durante o ano 1 e US$ 3 milhões durante o ano 2. Durante o ano 1, US$ 50 milhões em capital estão disponíveis para projetos, e US$ 20 milhões estão disponíveis durante o ano 2.

	VPL	Despesas do 1º ano	Despesas do 2º ano
Projeto 1	14	12	3
Projeto 2	17	54	7
Projeto 3	17	6	6
Projeto 4	15	6	2
Projeto 5	40	30	35
Projeto 6	12	6	6
Projeto 7	14	48	4
Projeto 8	10	36	3
Projeto 9	12	18	3

• Se não podemos realizar uma fração de um projeto, mas devemos realizar todo ou nenhum projeto, como podemos maximizar o NPV?

• Suponha que, se o Projeto 4 for realizado, o Projeto 5 deverá ser realizado. Como podemos maximizar o NPV?

• Uma editora está tentando determinar qual dos 36 livros deve publicar este ano. O Pressdata.xlsx de arquivo fornece as seguintes informações sobre cada livro:

  • Custos projetados de receita e desenvolvimento (em milhares de dólares)

  • Páginas em cada livro

  • Se o livro é voltado para uma audiência de desenvolvedores de software (indicado por um 1 na coluna E)

    Uma editora pode publicar livros que totalizam até 8.500 páginas este ano e deve publicar pelo menos quatro livros voltados para desenvolvedores de software. Como a empresa pode maximizar seu lucro?

Este artigo foi adaptado do Microsoft Office Excel 2007 Data Analysis and Business Modeling por Wayne L. Winston.

Este livro em estilo de sala de aula foi desenvolvido a partir de uma série de apresentações de Wayne Winston, um conhecido estatístico e professor de negócios especializado em aplicativos criativos e práticos do Excel.