Retorna a distribuição Poisson. Uma aplicação comum da distribuição Poisson é prever o número de eventos em um determinado período de tempo, como o número de carros que chega ao ponto de pedágio em um minuto.
Importante: Essa função foi substituída por uma ou mais funções novas que podem oferecer mais precisão e cujos nomes refletem melhor o seu uso. Embora essa função ainda esteja disponível para compatibilidade com versões anteriores, recomenda-se o uso das funções novas de agora em diante, pois ela pode não estar disponível em versões futuras do Excel.
Para saber mais sobre a nova função, consulte Função DIST.POISSON.
Sintaxe
POISSON(x,média,cumulativo)
A sintaxe da função POISSON tem os seguintes argumentos:
-
X Necessário. O número de eventos.
-
Média Necessário. O valor numérico esperado.
-
Cumulativo Necessário. Um valor lógico que determina a forma da distribuição de probabilidade fornecida. Se cumulativo for VERDADEIRO, POISSON retornará a probabilidade Poisson de que o número de eventos aleatórios estará entre zero e x inclusive; se FALSO, retornará a função massa da probabilidade Poisson de que o número de eventos será equivalente a x.
Comentários
-
Se x não for um número inteiro, será truncado.
-
Se x ou média não for numérica, POISSON retornará o #VALUE! valor de erro.
-
Se x < 0, POISSON retornará o #NUM! valor de erro.
-
Se a média < 0, POISSON retornará o #NUM! valor de erro.
-
POISSON é calculada da seguinte maneira.
Para cumulativo = FALSO:
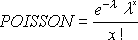
Para cumulativo = VERDADEIRO:
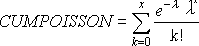
Exemplo
Copie os dados de exemplo da tabela a seguir e cole-os na célula A1 de uma nova planilha do Excel. Para as fórmulas mostrarem resultados, selecione-as, pressione F2 e pressione Enter. Se precisar, você poderá ajustar as larguras das colunas para ver todos os dados.
|
Dados |
Descrição |
|
|
2 |
O número de eventos |
|
|
5 |
A média esperada |
|
|
Fórmula |
Descrição (resultado) |
R esultado |
|
=POISSON(A2;A3;VERDADEIRO) |
A probabilidade cumulativa Poisson com os termos acima (0,124652) |
0,124652 |
|
=POISSON(A2;A3;FALSO) |
A função de probabilidade de massa Poisson com os termos acima (0,084224) |
0,084224 |










