Ten artykuł zawiera opis składni formuły i zastosowania funkcji TEST.Z w programie Microsoft Excel.
Zwraca prawdopodobieństwo testu dwustronnego z. Dla pewnej przyjętej w hipotezie średniej z populacji, μ0, funkcja TEST.Z zwraca prawdopodobieństwo, że średnia z próbki będzie większa od średniej z obserwacji w zbiorze danych (tablicy), tj. od obserwowanej średniej próbki.
W sekcji Spostrzeżenia poniżej opisano możliwości użycia funkcji TEST.Z w formule do obliczenia prawdopodobieństwa testu dwustronnego.
Ważne: Tę funkcję zamieniono na jedną lub więcej nowych funkcji, które mogą zapewniać większą dokładność i mają nazwy lepiej oddające ich przeznaczenie. Mimo że ta funkcja jest wciąż dostępna w celu zachowania zgodności z wcześniejszymi wersjami programu, należy rozważyć rozpoczęcie korzystania z nowych funkcji, ponieważ ta funkcja może być niedostępna w przyszłych wersjach programu Excel.
Aby uzyskać więcej informacji na temat nowej funkcji, zobacz temat Z.TEST, funkcja.
Składnia
TEST.Z(tablica;x;[sigma])
W składni funkcji TEST.Z występują następujące argumenty:
-
Tablica Argument wymagany. Tablica lub zakres danych, w stosunku do którego ma być testowana wartość x.
-
X Argument wymagany. Testowana wartość.
-
Sigma Argument opcjonalny. Odchylenie standardowe populacji (znane). W przypadku pomięcia tego argumentu stosowane będzie odchylenie standardowe próbki.
Spostrzeżenia
-
Jeśli argument tablica jest pusty, funkcja TEST.Z zwraca wartość błędu #N/D!.
-
Gdy wartość sigma nie zostanie pominięta, funkcja TEST.Z jest obliczana w następujący sposób:
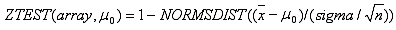
Natomiast gdy wartość sigma zostanie pominięta:
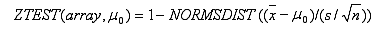
gdzie x jest średnią próbki ŚREDNIA(tablica); s jest odchyleniem standardowym próbki ODCH.STANDARDOWE(tablica); zaś n jest liczbą obserwacji w próbce ILE.LICZB(tablica).
-
Funkcja TEST.Z reprezentuje prawdopodobieństwo, że średnia z próbki będzie większa od obserwowanej wartości ŚREDNIA(tablica), gdy średnia bazowej populacji wynosi μ0. Z symetrii rozkładu normalnego wynika, że jeśli ŚREDNIA(tablica) < μ0, funkcja TEST.Z zwróci wartość większą niż 0,5.
-
Poniższej formuły programu Excel można użyć do obliczenia dwustronnego prawdopodobieństwa, że średnia z próbki będzie bardziej odległa od μ0 (w dowolnym kierunku) niż ŚREDNIA(tablica), gdy średnia bazowej populacji wynosi μ0:
=2 * MIN(TEST.Z(tablica;μ0;sigma), 1 - TEST.Z(tablica;μ0;sigma)).
Przykład
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Dane |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Formuła |
Opis (wynik) |
Wynik |
|
=TEST.Z(A2:A11;4) |
Wartość prawdopodobieństwa jednostronnego testu z dla powyższego zbioru danych i przyjętej wartości średniej z populacji równej 4 (0,090574) |
0,090574 |
|
=2 * MIN(TEST.Z(A2:A11;4);1 – TEST.Z(A2:A11;4)) |
Wartość prawdopodobieństwa dwustronnego testu z dla powyższego zbioru danych i przyjętej wartości średniej z populacji równej 4 (0,181148) |
0,181148 |
|
=TEST.Z(A2:A11;6) |
Wartość prawdopodobieństwa jednostronnego testu z dla powyższego zbioru danych i przyjętej wartości średniej z populacji równej 6 (0,863043) |
0,863043 |
|
=2 * MIN(TEST.Z(A2:A11;6);1 – TEST.Z(A2:A11;6)) |
Wartość prawdopodobieństwa dwustronnego testu z dla powyższego zbioru danych i przyjętej wartości średniej z populacji równej 6 (0,273913) |
0,273913 |










