Ten artykuł zawiera opis składni formuły i zastosowania funkcji PEARSON w programie Microsoft Excel.
Opis
Zwraca współczynnik korelacji liniowej Pearsona r. Jest to bezwymiarowy wskaźnik, którego wartość mieści się w zakresie od -1,0 do 1,0 włącznie, i odzwierciedla stopień liniowej zależności pomiędzy dwoma zestawami danych.
Składnia
PEARSON(tablica1;tablica2)
W składni funkcji PEARSON występują następujące argumenty:
-
Tablica1 Argument wymagany. Zbiór wartości niezależnych.
-
Tablica2 Argument wymagany. Zbiór wartości zależnych.
Spostrzeżenia
-
Argumenty powinny być liczbami lub nazwami, stałymi tablicowymi lub odwołaniami, które zawierają liczby.
-
Jeśli argument tablicowy lub odwołaniowy zawiera tekst, wartości logiczne lub puste komórki, to wartości te są ignorowane. Komórki o wartości zero są jednak włączane do obliczeń.
-
Jeżeli argumenty tablica1 i tablica2 są puste lub mają inną liczbę punktów danych, funkcja PEARSON zwraca wartość błędu #N/D!.
-
Wzór na współczynnik korelacji liniowej Pearsona, r, jest następujący:
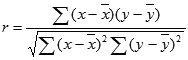
gdzie x i y są wynikami funkcji ŚREDNIA(tablica1) i ŚREDNIA(tablica2).
Przykład
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Dane |
||
|
Wartości niezależne |
Wartości zależne |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Formuła |
Opis (wynik) |
W ynik |
|
=PEARSON(A3:A7;B3:B7) |
Współczynnik korelacji momentu iloczynu Pearsona dla podanych powyżej zestawów danych (0,699379) |
0,699379 |










