Ten artykuł zawiera opis składni formuły i zastosowania funkcji MIRR w programie Microsoft Excel.
Opis
Zwraca wartość zmodyfikowanej wewnętrznej stopy zwrotu dla serii okresowych przepływów gotówkowych. Funkcja MIRR bierze pod uwagę jednocześnie koszt inwestycji oraz procent uzyskany z ponownego zainwestowania środków pieniężnych.
Składnia
MIRR(wartości;stopa_finansowa;stopa_reinwestycji)
W składni funkcji MIRR występują następujące argumenty:
-
Wartości Argument wymagany. Tablica lub odwołanie do komórek zawierających liczby. Te liczby reprezentują płatności (wartości ujemne) i przychód (wartości dodatnie) występujące w równych odstępach czasu.
-
Aby obliczyć zmodyfikowaną wewnętrzną stopę zwrotu, wartości muszą zawierać co najmniej jedną wartość dodatnią i jedną ujemną. W przeciwnym razie funkcja MIRR zwraca wartość #DIV/0! wartość błędu #ADR!.
-
Jeśli argument tablicowy lub odwołaniowy zawiera tekst, wartości logiczne lub puste komórki, to wartości te są ignorowane; komórki o wartości zero są jednak włączane do obliczeń.
-
-
Stopa_finansowa Argument wymagany. Stopa oprocentowania pobierana od środków używanych w przepływach gotówkowych.
-
Stopa_reinwestycji Argument wymagany. Stopa oprocentowania otrzymywana od reinwestowanych przepływów gotówkowych.
Spostrzeżenia
-
Funkcja MIRR używa ciągu wartości do interpretowania ciągu przepływów gotówkowych. Należy się upewnić, czy wartości określające wypłaty i przychody są wprowadzone we właściwej kolejności i z odpowiednimi znakami wartości (dodatnie dla kwot otrzymywanych, ujemne dla kwot wypłacanych).
-
Jeśli n to liczba przepływów gotówkowych, frate to stopa_finansowa, a rrate to stopa_reinwestycji, to formuła funkcji MIRR wygląda tak:
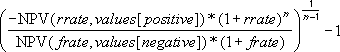
Przykład
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Dane |
Opis |
|
|
-120000 |
Koszt początkowy |
|
|
39000 |
Zwrot w pierwszym roku |
|
|
30000 |
Zwrot w drugim roku |
|
|
21000 |
Zwrot w trzecim roku |
|
|
37000 |
Zwrot w czwartym roku |
|
|
46000 |
Zwrot w piątym roku |
|
|
0,1 |
Roczna stopa oprocentowania dla pożyczki 120 000 |
|
|
0,12 |
Roczna stopa oprocentowania dla reinwestowanych zysków |
|
|
Formuła |
Opis |
Wynik |
|
=MIRR(A2:A7;A8;A9) |
Zmodyfikowana stopa zwrotu z inwestycji po pięciu latach |
13% |
|
=MIRR(A2:A5;A8;A9) |
Zmodyfikowana stopa zwrotu z inwestycji po trzech latach |
-5% |
|
=MIRR(A2:A7;A8;14%) |
Zmodyfikowana stopa zwrotu z inwestycji w okresie pięciu lat, przyjmując wartość 14% dla argumentu stopa_reinwestycji |
13% |










