Dit artikel bevat informatie over het gebruik van Oplosser, een Microsoft Excel-invoegtoepassing die u kunt gebruiken voor wat-als-analyse, om een optimale product mix te bepalen.
Hoe kan ik bepalen welke maandelijkse product mix winstgevend is?
Bedrijven dienen vaak de hoeveelheid van elk product te bepalen dat maandelijks dient te worden verlangd. In zijn eenvoudigste vorm dient het product mix -probleem te bepalen hoe u de hoeveelheid van elk product bepaalt dat binnen een maand moet worden geproduceerd om de winst te maximaliseren. De product mix moet doorgaans voldoen aan de volgende beperkingen:
-
Product mix mag niet meer resources gebruiken dan beschikbaar is.
-
Er geldt een beperkte vraag voor elk product. We kunnen niet meer producten produceren gedurende een maand dan de vraag, omdat de overschot van de overbelasting wordt verspild (zoals een bederfelijke medicijn).
U kunt nu het volgende voorbeeld van het productmix probleem oplossen. U vindt de oplossing voor dit probleem in de Prodmix.xlsx bestand, weergegeven in afbeelding 27-1.
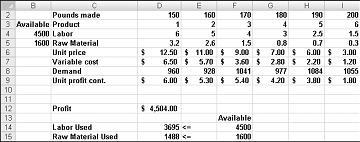
Stel dat we voor een farmaceutisch bedrijf werken met zes verschillende producten op hun eigen bedrijf. Voor de productie van elk product is arbeid en grond materiaal vereist. In rij 4 in afbeelding 27-1 wordt het tijdstip van de arbeid aangegeven die nodig is voor het maken van een pond van elk product, en de rij 5 toont de kilo grams producten die nodig zijn voor het maken van een pond van elk product. Als u bijvoorbeeld een pond van product 1 wilt produceren, moet u zes uur arbeids arbeid en 3,2 lbs van grondstof produceren. Voor elk medicijn wordt de prijs per pond gegeven in rij 6, de kostprijs per pond opgegeven in rij 7 en de winstbijdrage per pond wordt uitgedrukt in rij 9. Product 2 wordt bijvoorbeeld verkocht voor $11,00 per pond, de kostprijs van $5,70 per pond, en draagt een bijdrage aan $5,30 winst per pond. De vraag van de maand voor elk medicijn wordt gegeven in rij 8. Zo is vraag voor product 3 1041 pond. Deze maand zijn 4500 uur arbeid en 1600 lbs van grondstof vrij. Hoe kan dit bedrijf de maandelijkse winst maximaliseren?
Als we op de hoogte zijn van Excel Oplosser, kunnen we dit probleem verhelpen door een werkblad te construeren, zodat het winst-en Resourcegebruik van de product mix kan worden bijgehouden. Vervolgens gebruiken we de proefversie en-fout om de winst te bekrachtigen zonder dat u meer arbeid of grondstof gebruik hoeft te maken dan is beschikbaar, en zonder dat er een medicijn voor de vraag wordt geproduceerd. In deze procedure wordt Oplosser alleen in de fase proefversie en de fout fase gebruikt. In essentie is Oplosser een optimaliserings engine waarmee het zoeken naar een proefversie en fouten kan worden uitgevoerd.
Een sleutel voor het oplossen van het probleem met het productmix is het efficiënt te berekenen van het Resourcegebruik en de winst die is gekoppeld aan een bepaald product mix. Een belangrijk hulpmiddel voor het maken van deze berekening is de functie SOMPRODUCT. Met de functie SOMPRODUCT worden corresponderende waarden in celbereiken vermenigvuldigd en wordt de som van deze waarden als resultaat gegeven. Elk celbereik dat wordt gebruikt in een SOMPRODUCT-evaluatie, moet dezelfde afmetingen hebben, wat betekent dat u SOMPRODUCT met twee rijen of twee kolommen kunt gebruiken, maar niet één kolom en één rij.
Als voorbeeld van het gebruik van de functie SOMPRODUCT in het voorbeeld van de productmix, gaan we proberen het Resourcegebruik te berekenen. Onze arbeid wordt berekend door
(Arbeid gebruikt per pond van medicijn 1) * (medicijn 1 pond voortgebracht) + (Arbeid gebruikt per pond van medicijn 2) * (medicijn 2 pond voortgebracht) +... (Arbeid gebruikt per pond van medicijn 6) * (medicijn 6 pond geproduceerd)
We kunnen het werk voor arbeids gebruik op een nog veelere manier berekenen als D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4. Ook kan het gebruik van onbewerkte materialen worden berekend als D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + I2 * i5. Het invoeren van deze formules in een werkblad duurt echter niet voor zes producten. U kunt zien hoe lang het duurt voordat u met een bedrijf werkte dat, bijvoorbeeld 50-producten, op hun eigen bedrijf werd vervaardigd. Een veel eenvoudige manier om arbeid en grondstofverbruik te berekenen is het kopiëren van D14 naar D15 de formule SOMPRODUCT ($D $2: $I $2, D4: I4). Met deze formule wordt de D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4 (wat is onze arbeidsverbruik), maar u kunt nog veel makkelijker invoeren. Let op dat ik het $-teken met het bereik D2: I2, zodat wanneer ik de formule Kopieer, zodat ik de product mix van rij 2 nog moet vastleggen. De formule in cel D15 rekent grondstofverbruik.
Onze winst wordt op een soortgelijke manier bepaald door
(Winst per pond voor medicijn 1) * (medicijn 1 pond geproduceerd) + (Medicijn 2 winst per pond) * (medicijn 2 pond geproduceerd) +... (Medicijn 6 winst per pond) * (medicijn 6 pond geproduceerd)
Winst in cel D10 met de formule SOMPRODUCT (D9: i9, $D $2: $I $2)is eenvoudig te berekenen.
We kunnen nu de drie onderdelen van ons product mix Oplosser-model identificeren.
-
Doelcel. Ons doel is de winstgevendheid te maximaliseren (berekend in cel D10).
-
Cellen wijzigen. Het aantal kilo kilos van elk product (vermeld in het cellenbereik D2: I2)
-
Beperkingen. We hebben de volgende beperkingen:
-
Gebruik niet meer werk of onkosten grondstoffen. Dat wil zeggen: de waarden in de cellen D14: D15 (de gebruikte resources) moeten kleiner zijn dan of gelijk zijn aan de waarden in de cellen F14: F15 (de beschikbare bronnen).
-
Produceert geen meer van een drugs dan met de vraag. Dat wil zeggen: de waarden in de cellen D2: I2 (Euro's gemaakt van elk medicijn) moeten kleiner zijn dan of gelijk zijn aan de vraag voor elk medicijn (vermeld in cel D8: I8).
-
Er kan geen sprake zijn van een negatieve hoeveelheid drugs.
-
Ik laat u zien hoe u de doelcel, het wijzigen van cellen en beperkingen in Oplosser invoert. Vervolgens hoeft u niet te klikken op de knop oplossen om een product mix met winst te zoeken.
Als u wilt beginnen, klikt u op het tabblad gegevens en klikt u in de groep analyse op Oplosser.
Opmerking: Zoals beschreven in hoofdstuk 26, "een inleiding tot optimalisering met Excel Oplosser", is ' Oplosser ' geïnstalleerd door op de Microsoft Office-knop te klikken, vervolgens op Opties voor Excel en vervolgens op invoegtoepassingen. Klik in de lijst beheren op Excel-invoegtoepassingen, schakel het selectievakje invoegtoepassing Oplosser in en klik vervolgens op OK.
Het dialoogvenster parameters van Oplosser wordt weergegeven, zoals wordt weergegeven in afbeelding 27-2.
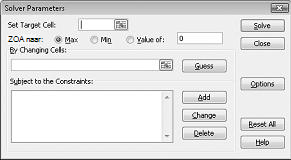
Klik in het vak doelcel instellen en selecteer vervolgens onze winst cel (cel D10). Klik op het vak door veranderende cellen en wijs het bereik D2: I2 aan, dat de Euro's bevat van elk medicijn. In het dialoogvenster ziet u nu afbeelding 27-3.
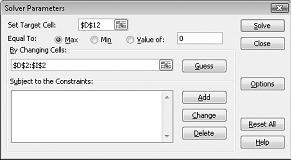
U kunt nu beperkingen toevoegen aan het model. Klik op de knop toevoegen. U ziet het dialoogvenster beperking toevoegen, dat wordt weergegeven in afbeelding 27-4.
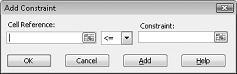
Als u de beperkingen voor Resourcegebruik wilt toevoegen, klikt u in het vak celverwijzing en selecteert u het bereik D14: D15. Selecteer <= in de middelste lijst. Klik op het vak CONSTRAINT en selecteer het celbereik F14: F15. Het dialoogvenster beperking toevoegen moet er nu zo uitzien als in afbeelding 27-5.
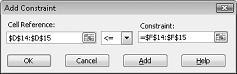
Wanneer Oplosser verschillende waarden voor de veranderende cellen probeert te gebruiken, worden alleen combinaties weergegeven die voldoen aan beide D14<= F14 (arbeid verbruikt minder dan of gelijk aan de beschikbare arbeid) en D15<= F15 (grondstofverbruik is kleiner dan of gelijk aan het onbewerkte materiaal) wordt beschouwd. Klik op toevoegen om de vraag beperkingen in te voeren. Vul het dialoogvenster beperking toevoegen in, zoals wordt weergegeven in afbeelding 27-6.
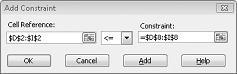
Door deze beperkingen toe te voegen, zorgt u ervoor dat alleen combinaties die voldoen aan de volgende parameters worden gebruikt:
-
D2<= D8 (het bedrag dat is gemaakt van medicijn 1 is kleiner dan of gelijk aan de vraag voor medicijn 1)
-
E2<= E8 (de hoeveelheid vervaardigd van medicijn 2 is kleiner dan of gelijk aan de vraag voor medicijn 2)
-
F2<= F8 (het bedrag dat is gemaakt van medicijn 3 is kleiner dan of gelijk aan de vraag voor medicijn 3)
-
G2<= G8 (het gemaakte bedrag van medicijn 4 is kleiner dan of gelijk aan de vraag voor medicijn 4)
-
H2<= H8 (het gemaakte bedrag van medicijn 5 is kleiner dan of gelijk aan de vraag voor medicijn 5)
-
I2<= i8 (het gemaakte bedrag van medicijn 6 is kleiner dan of gelijk aan de vraag voor medicijn 6)
Klik op OK in het dialoogvenster beperking toevoegen. Het Oplosser-venster moet er nu zo uitzien als in afbeelding 27-7.
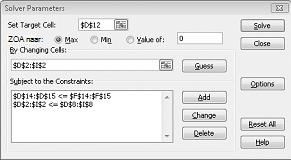
In het dialoogvenster Opties voor Oplosser wordt de beperking ingevoerd waarmee cellen wijzigen in niet-negatief moeten zijn. Klik in het dialoogvenster Parameters Oplosser op de knop Opties. Selecteer het selectievakje lineair model aannemen en het selectievakje niet-negatief, zoals weergegeven in afbeelding 27-8, op de volgende pagina. Klik op OK.
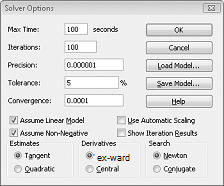
Als u wilt controleren of het selectievakje niet-negatieve waarden opneemt, wordt u aangeraden alleen combinaties van veranderende cellen te bezorgen, waarbij elke veranderende cel een niet-negatieve waarde in beoordeelt. We hebben het selectievakje lineair model aannemen uitgeschakeld, omdat het product mix van een speciaal type probleem met Oplosser een lineair modelwordt genoemd. In feite is een Solver-model lineair onder de volgende voorwaarden:
-
De doelcel wordt berekend door de termen van het formulier (cel wijzigen) * (constante)op te tellen.
-
Elke beperking voldoet aan de vereisten voor lineair model. Dit betekent dat elke beperking wordt geëvalueerd door samen de termen van het formulier (veranderende cel) * (constante) en de totalen te vergelijken met een constante.
Waarom is dit Oplosser-probleem lineair? De doelcel (winst) wordt berekend als
(Winst per pond voor medicijn 1) * (medicijn 1 pond geproduceerd) + (Medicijn 2 winst per pond) * (medicijn 2 pond geproduceerd) +... (Medicijn 6 winst per pond) * (medicijn 6 pond geproduceerd)
Bij deze berekening wordt een patroon gevolgd waarbij de waarde van de doelcel wordt afgeleid door samen termen van het formulier (veranderende cel) * (constante)toe te voegen.
Onze arbeid-beperking wordt geëvalueerd door de waarde te vergelijken die is afgeleid van (arbeidsverbruik per pond van medicijn 1) * (medicijn 1 pond geproduceerd) + (arbeid verbruik per pond van medicijn 2) +... (Arbeid USEd per pond van medicijn 6) * (medicijn 6 pond voortgebracht) tot de beschikbare arbeid.
Daarom wordt de beperking voor de arbeid geëvalueerd door de termen van het formulier (cel wijzigen) * (constante) te combineren en de totalen te vergelijken met een constante. De beperking arbeid en de grondstof beperking voldoen aan de vereisten voor lineair model.
Onze Aanvraagbeperkingen hebben de vorm
(Medicijn 1 vervaardigd) <= (vraag voor medicijn 1) (Medicijn 2 geproduceerd) <= (medicijn 2 vraag) § (Medicijn 6 vervaardigd) <= (medicijn 6 vraag)
Elke aanvraagbeperking voldoet ook aan de vereisten voor lineair model, omdat elk wordt geëvalueerd door het toevoegen van de termen van het formulier (veranderende cel) * (constante) en de vergelijking van de totalen met een constante.
Hoe kan ik zien dat ons product mix een lineair model is, waarom we het willen doen?
-
Als een Oplosser-model lineair is en we selecteren als lineair model, is Oplosser gegarandeerd de optimale oplossing voor het Oplosser-model. Als een Solver-model niet lineair is, kan Oplosser de optimale oplossing mogelijk niet vinden.
-
Als een Solver-model lineair is en we selecteren als lineair model, moet Oplosser een zeer efficiënt algoritme (de simplex-methode) gebruiken om de optimale oplossing van het model te zoeken. Als een Solver-model lineair is en we niet selecteren om het voor lineair model te selecteren, gebruikt Oplosser een zeer ondoelmatig algoritme (de GRG2-methode) en kan de optimale oplossing van het model niet worden gevonden.
Nadat u op OK hebt geklikt in het dialoogvenster Opties voor Oplosser, gaat u terug naar het hoofdvenster van Oplosser, dat eerder werd weergegeven in afbeelding 27-7. Wanneer we op oplossen klikken, wordt er een optimale oplossing (indien aanwezig) voor ons productmixmodel berekend. Zoals u in hoofdstuk 26 hebt uiteengezet, is een optimale oplossing voor het product mix-model een set gewijzigde celwaarden (kilo ponden van elk medicijn) die de winst in de reeks van alle bruikbare oplossingen optimaliseren. Een bruikbare oplossing is een reeks veranderende celwaarden die voldoen aan alle beperkingen. De veranderende celwaarden in afbeelding 27-9 vormen een beschikbare oplossing omdat alle productieniveaus niet-negatief zijn, de productieniveaus niet groter zijn dan de vraag en het Resourcegebruik niet meer dan de beschikbare bronnen.
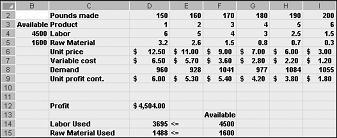
De veranderende celwaarden die in afbeelding 27-10 op de volgende pagina worden weergegeven, duiden op een onhaalbaar oplossing om de volgende redenen:
-
We produceren meer van medicijn 5 dan de vraag daarvoor.
-
We gebruiken meer arbeid dan de beschikbare functies.
-
U gebruikt meer onbewerkte materialen dan wat er beschikbaar is.
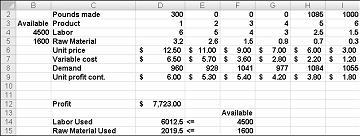
Nadat u op oplossen hebt geklikt, vindt u met Oplosser snel de optimale oplossing die wordt weergegeven in afbeelding 27-11. U moet Oplosser-oplossing behouden selecteren om de optimale oplossings waarden in het werkblad te behouden.
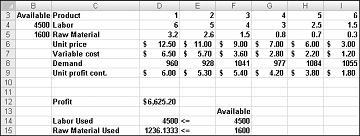
Onze drugs maatschappij kan zijn maand winst op een niveau van $6.625,20 maximaliseren door 596,67 pond van medicijn 4, 1084 lbs van medicijn 5 en geen andere drugs te produceren. We kunnen niet bepalen of we de maximum winst met $6.625,20 op andere manieren kunnen bereiken. We kunnen er ook voor zorgen dat u deze maand niet meer dan $6.627,20 kunt maken, met onze beperkte informatiebronnen en aanvraag.
U dient eerst te voldoen aan de vraag voor elk product. (Zie het werkblad geen bruikbare oplossing in de Prodmix.xlsx bestand.) We moeten vervolgens onze Aanvraagbeperkingen wijzigen van D2: I2<= D8: I8 naar D2: I2>= D8: I8. Open Oplosser, selecteer de beperking D2: I2<= D8: I8 en klik vervolgens op wijzigen. Het dialoogvenster beperking wijzigen, weergegeven in afbeelding 27-12, wordt weergegeven.
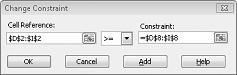
Selecteer >= en klik vervolgens op OK. U wordt nu aangeraden alleen de celwaarden te wijzigen die aan alle aanvragen voldoen. Wanneer u op oplossen klikt, wordt het bericht ' Oplosser kon geen bruikbare oplossing gevonden ' weergegeven. Dit bericht betekent niet dat we een fout hebben gemaakt in ons model, maar in plaats daarvan met onze beperkte bronnen, kunnen we niet aan de vraag voor alle producten voldoen. Oplosser vertelt ons dat, als we willen voldoen aan de vraag van elk product, meer arbeid, meer grondstof of meer van beide producten moeten worden toegevoegd.
Laten we eens kijken wat er gebeurt als we onbeperkt vragen stellen voor elk product en we sta toe dat ze van elk medicijn een negatieve hoeveelheid worden voortgebracht. (Dit probleem met Oplosser wordt weergegeven op het werkblad waarden van de instelling niet samenstellen in de Prodmix.xlsx.) Om de optimale oplossing voor deze situatie te vinden, opent u Oplosser, klikt u op de knop Opties en schakelt u het selectievakje niet-negatief uit. Selecteer in het dialoogvenster parameters van Oplosser de aanvraagbeperking D2: I2<= D8: I8 en klik op verwijderen om de beperking te verwijderen. Wanneer u op oplossen klikt, wordt het bericht ' de celwaarden instellen wordt niet geconvergeerd ' geretourneerd. Dit bericht houdt in dat als de doelcel wordt gemaximaliseerd (zoals in ons voorbeeld), er haalbaar oplossingen zijn met willekeurige, grote waarden voor de doelcellen. (Als de doelcel moet worden geminimaliseerd, betekent het bericht ' celwaarden instellen niet convergeren ' betekent dat er een willekeurige oplossing is voor willekeurige klein waarden van de doelcellen.) Met een negatieve voortbrenging van een medicijn, in ons geval van een negatieve voortbrenging van een medicijn, hebben we de middelen voor het maken van bronnen voor het produceren van een willekeurige grote hoeveelheid andere drugs. Met onze onbeperkt behoeftings functie kunnen we onbeperkt winst doen. U kunt in een echte situatie geen oneindig bedrag betalen. Als u bijvoorbeeld ' waarden instellen, geen convergeert ' ziet, heeft het model een fout.
-
Stel dat ons farmaceutisch bedrijf $1 gedurende een uur van de arbeid met een hoeveelheid werk per uur tot 500 uur aan de arbeid mag kopen. Hoe kan ik winst optimaliseren?
-
Bij een chip fabriek produceren vier technici (A, B, C en D) drie producten (producten 1, 2 en 3). Deze maand kan de chip fabrikant 80 verkopen van product 1, 50 eenheden van product 2 en hooguit 50 stuks van product 3. Technici kunnen alleen producten 1 en 3 maken. Technicus B kan alleen producten 1 en 2 maken. Technicus C kan alleen product 3 maken. Technicus D kan alleen product 2 maken. Voor elke eenheid wordt de volgende winst in de producten bijgemaakt: product 1, $6; Product 2, $7; en product 3, $10. De tijd (in uren) die elke technicus moet produceren een product is als volgt:
Product
Technicus A
Technicus B
Technicus C
Technicus D
1
2
2,5
Kan niet
Kan niet
2
Kan niet
3
Kan niet
3,5
3
3
Kan niet
4
Kan niet
-
Elke medewerker kan tot 120 uur per maand werken. Hoe kan de chip fabrikant de maandelijkse winst maximaliseren? U kunt ook een gebroken aantal eenheden produceren.
-
Een computer fabriek produceert muizen, toetsenborden en joysticks voor videogames. De winst per eenheid, de hoeveelheid werk per eenheid, de maandelijkse vraag en de tijdseenheid per eenheid worden in de volgende tabel opgenomen:
Muizen
Borden
Joysticks
Winst/eenheid
$8
$11
$9
Arbeidsverbruik/eenheid
2 uur
3 uur
.24 uur
Tijdseenheid van de machine
.04 uur
.055 uur
.04 uur
Maandelijks verzoek
15.000
27.000
11.000
-
Voor elke maand zijn er een totaal van 13.000 arbeidsuren en 3000 uur van de machinetijd beschikbaar. Hoe kan de fabrikant de maandelijkse winstbijdrage van de plant maximaliseren?
-
Oplossing voor het voorbeeld van ons medicijn, met uitgaand dat aan elk medicijn een minimum vraag van 200-eenheden is voldaan.
-
Jason laat de ruit Bracelets, Necklaces en Earrings. Hij wil tot maximaal 160 uur per maand werken. Hij heeft 800 ounces met ruiten. Hieronder vindt u de winst, de arbeid en de ounce van de ruiten die nodig zijn om elk product te produceren. Als de vraag voor elk product onbeperkt is, hoe kan Jason die winst maximaliseren?
Product
Eenheids winst
Arbeidsuren per eenheid
Ounces diamant per eenheid
Bracelet
€ 300
.35
1,2
Necklace
$ 200
15
.75
Earrings
€ 100
0,05
0,5










