Bruke Problemløser til kapitalbudsjettering

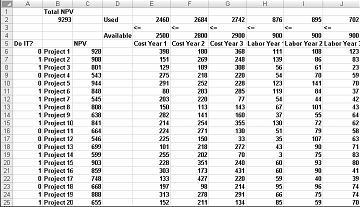
De fleste selskaper ønsker å gjennomføre prosjekter som bidrar med størst netto nåverdi (NNV), underlagt begrensede ressurser (vanligvis kapital og arbeidskraft). La oss si at et programvareutviklingsselskap prøver å finne ut hvilke av 20 programvareprosjekter det skal gjennomføre. NNV (i millioner av dollar) bidratt av hvert prosjekt samt kapitalen (i millioner av dollar), og antall programmerere som trengs i løpet av hvert av de neste tre årene, gis i regnearket Grunnleggende modell i filen Capbudget.xlsx, som vises i figur 30-1 på neste side. Project 2 gir for eksempel usd 908 millioner. Det krever $ 151 millioner i løpet av år 1, $ 269 millioner i løpet av år 2, og $ 248 millioner i løpet av år 3. Project 2 krever 139 programmerere i løpet av år 1, 86 programmerere i løpet av år 2 og 83 programmerere i løpet av år 3. Cellene E4:G4 viser kapitalen (i millioner av dollar) som er tilgjengelig i løpet av hvert av de tre årene, og cellene H4:J4 angir hvor mange programmerere som er tilgjengelige. For eksempel, i løpet av år 1 opp til $ 2,5 milliarder i kapital og 900 programmerere er tilgjengelige.

Selskapet må avgjøre om det skal gjennomføres hvert prosjekt. La oss anta at vi ikke kan gjennomføre en brøkdel av et programvareprosjekt. Hvis vi tildeler 0,5 av de nødvendige ressursene, har vi for eksempel et arbeidsprogram som gir oss omsetning på USD 0!

Trikset i modelleringssituasjoner der du enten gjør eller ikke gjør noe, er å bruke binære endringsceller. En binær endringscelle er alltid lik 0 eller 1. Når en binær endringscelle som tilsvarer et prosjekt er lik 1, gjør vi prosjektet. Hvis en binær endringscelle som tilsvarer et prosjekt er lik 0, gjør vi ikke prosjektet. Du konfigurerer Problemløser til å bruke et område med binære endringsceller ved å legge til en begrensning. Merk de endrede cellene du vil bruke, og velg deretter Intervall fra listen i dialogboksen Legg til betingelse.

Med denne bakgrunnen er vi klare til å løse problemet med valg av programvareprosjekt. Som alltid med en Problemløser-modell begynner vi med å identifisere målcellen, endringscellene og begrensningene.

• Målcelle. Vi maksimerer NNV-en som genereres av valgte prosjekter.

• Endre celler. Vi ser etter en binær endringscelle på 0 eller 1 for hvert prosjekt. Jeg har plassert disse cellene i området A6:A25 (og har kalt området doit). En 1 i celle A6 angir for eksempel at vi gjennomfører Project 1. en 0 i celle C6 indikerer at vi ikke gjennomfører Project 1.

• Begrensninger. Vi må sørge for at for hvert år t (t= 1, 2, 3), år t kapital brukes er mindre enn eller lik År t kapital tilgjengelig, og År t arbeidskraft brukes er mindre enn eller lik År t arbeidskraft tilgjengelig.

Som du kan se, må regnearket vårt beregne for alle prosjekter som NNV, kapitalen som brukes årlig, og programmererne som brukes hvert år. I celle B2 bruker jeg formelen SUMMERPRODUKT(doit,NNV) til å beregne total NNV generert av valgte prosjekter. (Områdenavnet NNV refererer til området C6:C25.) For hvert prosjekt med 1 i kolonne A plukker denne formelen opp NNV for prosjektet, og for hvert prosjekt med 0 i kolonne A plukker ikke denne formelen opp NNV for prosjektet. Derfor er vi i stand til å beregne NNV for alle prosjekter, og målcellen vår er lineær fordi den beregnes ved å summere termer som følger skjemaet (endrer celle)*(konstant). På lignende måte beregner jeg kapitalen som brukes hvert år, og arbeidet som brukes hvert år ved å kopiere fra E2 til F2:J2 formelen SUMMERPRODUKT(doit,E6:E25).

Jeg fyller nå ut dialogboksen Problemløserparametere som vist i figur 30-2.

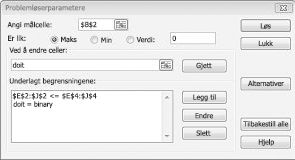
Målet vårt er å maksimere NNV for valgte prosjekter (celle B2). Våre endringsceller (området kalt doit) er de binære endringscellene for hvert prosjekt. Begrensningen E2:J2<=E4:J4 sikrer at kapitalen og arbeidskraften som brukes i løpet av hvert år, er mindre enn eller lik den tilgjengelige kapitalen og arbeidskraften. Hvis du vil legge til betingelsen som gjør endringscellene binære, klikker jeg Legg til i dialogboksen Problemløserparametere, og velger deretter Intervall fra listen midt i dialogboksen. Dialogboksen Legg til betingelse skal vises som vist i figur 30-3.

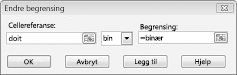
Modellen vår er lineær fordi målcellen beregnes som summen av termer som har skjemaet (endre celle)*(konstant) og fordi begrensningene for ressursbruk beregnes ved å sammenligne summen av (endringsceller)*(konstanter) med en konstant.

Når dialogboksen Problemløserparametere er fylt ut, klikker du Løs, og vi har resultatene vist tidligere i figur 30-1. Selskapet kan få maksimalt 9293 millioner dollar (9,293 milliarder dollar) ved å velge Prosjekter 2, 3, 6–10, 14–16, 19 og 20.

Noen ganger har prosjektvalgmodeller andre begrensninger. Anta for eksempel at hvis vi velger Project 3, må vi også velge Project 4. Siden den gjeldende optimale løsningen velger Project 3, men ikke Project 4, vet vi at den gjeldende løsningen ikke kan forbli optimal. Hvis du vil løse dette problemet, legger du ganske enkelt til betingelsen om at den binære endringscellen for Project 3 er mindre enn eller lik den binære endringscellen for Project 4.

Du finner dette eksemplet i regnearket Hvis 3 og 4 i filen Capbudget.xlsx, som vises i figur 30-4. Celle L9 refererer til den binære verdien som er relatert til Project 3, og celle L12 til binærverdien som er relatert til Project 4. Ved å legge til begrensningen L9<=L12, hvis vi velger Project 3, er L9 lik 1, og begrensningen tvinger L12 (binærfilen for Project 4) til å være lik 1. Begrensningen må også la binærverdien være i den endrede cellen i Project 4 ubegrenset hvis vi ikke velger Project 3. Hvis vi ikke velger Project 3, er L9 lik 0, og betingelsen tillater at binærfilen for Project 4 er lik 0 eller 1, som er det vi ønsker. Den nye optimale løsningen vises i figur 30-4.

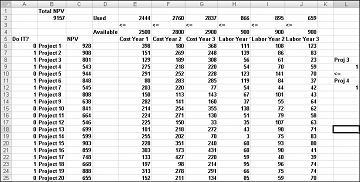
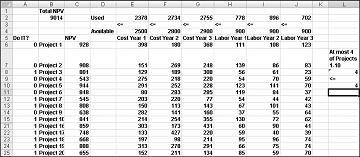
En ny optimal løsning beregnes hvis det å velge Project 3 betyr at vi også må velge Project 4. La oss nå anta at vi bare kan utføre fire prosjekter blant prosjekter fra 1 til 10. (Se regnearket Maksimalt fire av P1–P10 , vist i figur 30–5.) I celle L8 beregner vi summen av binærverdiene som er knyttet til Prosjekter 1 til og med 10 med formelen SUMMER(A6:A15). Deretter legger vi til begrensningen L8<=L10, som sikrer at maksimalt 4 av de første 10 prosjektene er valgt. Den nye optimale løsningen vises i figur 30-5. NPV har falt til $ 9.014 milliarder.

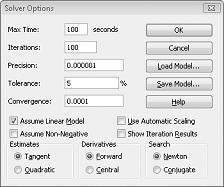
Lineære problemløsermodeller der noen eller alle endringsceller må være binære eller heltall, er vanligvis vanskeligere å løse enn lineære modeller der alle endringsceller kan være brøker. Derfor er vi ofte fornøyd med en nesten optimal løsning på et binært programmeringsproblem eller heltall. Hvis Problemløser-modellen kjører i lang tid, bør du vurdere å justere toleranseinnstillingen i dialogboksen Alternativer for problemløser. (Se figur 30-6.) En toleranseinnstilling på 0,5 % betyr for eksempel at Problemløser stopper første gang den finner en mulig løsning som er innenfor 0,5 prosent av den teoretiske optimale målcelleverdien (den teoretiske optimale målcelleverdien er den optimale målverdien som blir funnet når binær- og heltallsbetingelsene utelates). Ofte står vi overfor et valg mellom å finne et svar innen 10 prosent av optimalt på 10 minutter eller å finne en optimal løsning om to uker med datamaskintid! Standard toleranseverdi er 0,05 %, noe som betyr at Problemløser stopper når den finner en målcelleverdi innenfor 0,05 prosent av den teoretiske optimale målcelleverdien.

1. Et selskap har ni prosjekter under vurdering. NNV som legges til av hvert prosjekt og kapitalen som kreves av hvert prosjekt i løpet av de neste to årene, vises i tabellen nedenfor. (Alle tall er i millioner.) Project 1 vil for eksempel legge til USD 14 millioner i NNV og kreve utgifter på usd 12 millioner i løpet av år 1 og 3 millioner i løpet av år 2. I løpet av år 1 er $ 50 millioner i kapital tilgjengelig for prosjekter, og $ 20 millioner er tilgjengelig i løpet av år 2.

	NNV	Utgifter for 1. år	Utgifter for år 2
Prosjekt 1	14	12	3
Prosjekt 2	17	54	7
Prosjekt 3	17	6	6
Prosjekt 4	15	6	2
Prosjekt 5	40	30	35
Prosjekt 6	12	6	6
Prosjekt 7	14	48	4
Prosjekt 8	10	36	3
Prosjekt 9	12	18	3

• Hvis vi ikke kan gjennomføre en brøkdel av et prosjekt, men må gjennomføre enten hele eller ingen av et prosjekt, hvordan kan vi maksimere NPV?

• La oss si at hvis Project 4 utføres, må Project 5 gjennomføres. Hvordan kan vi maksimere NNV?

• Et forlag prøver å finne ut hvilke av 36 bøker det skal publisere i år. Filen Pressdata.xlsx gir følgende informasjon om hver bok:

  • Forventede inntekter og utviklingskostnader (i tusenvis av dollar)

  • Sider i hver bok

  • Om boken er rettet mot et publikum av programvareutviklere (angitt med en 1 i kolonne E)

    Et forlag kan publisere bøker på opptil 8500 sider i år og må publisere minst fire bøker rettet mot programvareutviklere. Hvordan kan selskapet maksimere fortjenesten?

Denne artikkelen er tilpasset fra Microsoft Office Excel 2007 Data Analysis and Business Modeling av Wayne L. Winston.

Denne boken i klasseromstil ble utviklet fra en rekke presentasjoner av Wayne Winston, en velkjent statistiker og forretningsprofessor som spesialiserer seg på kreative, praktiske anvendelser av Excel.