Šajā tēmā ir aprakstītas dažādas tendences līknes opcijas, kas ir pieejamas sistēmā Office.
Izmantojiet šī tipa tendenču līkni, lai izveidotu taisnu līniju, kas vislabāk atbilst vienkāršām lineārām datu kopām. Jūsu dati ir lineāri, ja tā datu punktu modelis izskatās kā līnija. Lineāra tendenču līkne parasti norāda, ka vienmērīgi palielinās vai samazinās.
Lineāra tendenču līkne izmanto šo vienādojumu, lai aprēķinātu taisnei mazākos kvadrātiņus:
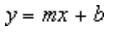
kur m ir slīpums un b ir krustpunkts.
Tālāk sniegtā lineārā tendenču līkne norāda, ka pārdošanas apjoms ir konsekventi palielināts 8 gadu periodā. Ievērojiet, ka R kvadrāta vērtība (skaitlis no 0 līdz 1, kas parāda, cik tuvu tendenču līknes aptuvenajām vērtībām atbilst faktiskajiem datiem) ir 0,9792, kas atbilst datiem.
Šī tendenču līkne ir vislabāk piemērota izliektas līnijas rādīšanai, ja datu izmaiņu ātrums ātri palielinās vai samazinās un pēc tam samazinās. Logaritmiskā tendences līkne var izmantot negatīvas un pozitīvas vērtības.
Logaritmiskā tendenču līkne izmanto šo vienādojumu, lai aprēķinātu mazāko kvadrātu atbilstību punktos:
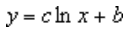
kur c un b ir konstantes un ln ir naturālā logaritma funkcija.
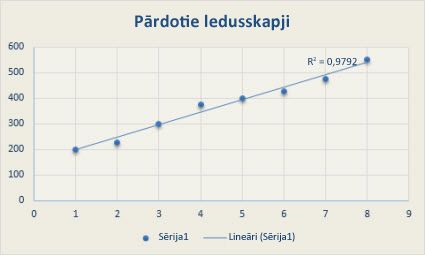
Tālāk redzamais logaritmiskais tendences līkne parāda prognozēto dzīvnieku populācijas augšanu fiksētā vietā, kur samazināts populācijas līmenis kā atstarpe zvēriem. Ņemiet vērā, ka R kvadrātā vērtība ir 0,933, kas ir relatīvi laba līnijas ietilpināšana datiem.
Šī tendences līkne ir noderīga, ja jūsu dati ir interfeisā. Piemēram, strādājot ar ieguvumiem un zaudējumiem lielā datu kopā. Polinoma secību var noteikt pēc datu svārstību skaita vai pēc līknē parādīto līkņu (kalnos un ielejās) parādīšanās. Parasti order 2 polynomial trendline has only one hill or valley, an Order 3 has one or two hills or valleys, and an Order 4 has up three hills or valleys.
Polinoma vai ieliekta tendenču līkne izmanto šo vienādojumu, lai aprēķinātu mazāko kvadrātu atbilstību punktiem:
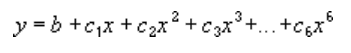
kur b un 
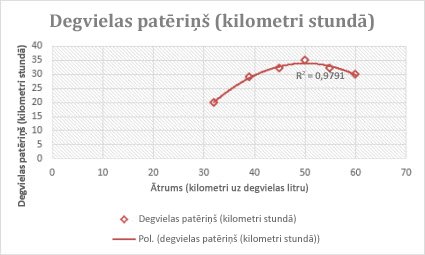
Tālāk redzamais 2. secības polinomu tendenču līkne (viens kalns) parāda relāciju starp braukšanas ātrumu un degvielas patēriņu. Ievērojiet, ka R kvadrāta vērtība ir 0,979, kas ir tuvu 1, lai rindiņa labi atbilstu datiem.
Līknes parādīšana Šī tendenču līkne ir noderīga datu kopām, kas salīdzina mērījumus, kuri palielinās ar noteiktu ātrumu. Piemēram, sacensību automašīnas paātrināšana ar 1 sekundes intervālu. Tendences līkni nevar izveidot, ja datos ir nulle vai negatīvas vērtības.
Tendenču līkne izmanto šo vienādojumu, lai aprēķinātu mazākos kvadrātus punktos:
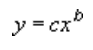
kur c un b ir konstantes.
Piezīme.: Šī opcija nav pieejama, ja datos ir negatīvas vai nulles vērtības.
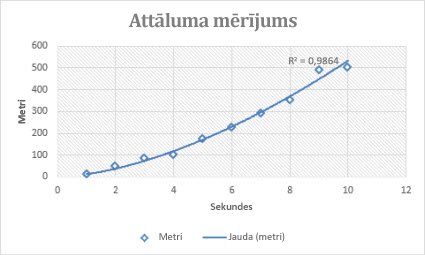
Tālāk redzamais attāluma mērījumu diagramma parāda attālumu metriem pa sekundēm. Enerģijas tendences līkne skaidri parāda pieaugošu paātrinātāju. Ņemiet vērā, ka R kvadrātā vērtība ir 0,986, kas ir gandrīz ideāli piemērota datiem rindā.
Izliektu līniju rāda, šī tendences līkne ir noderīga, ja datu vērtības palielinās vai samazinās ar pastāvīgi pieaugošu ātrumu. Nevar izveidot eksponenciālu tendences līkni, ja datos ir nulle vai negatīvas vērtības.
Eksponenciālā tendenču līkne izmanto šo vienādojumu, lai aprēķinātu mazāko kvadrātu atbilstību punktos:
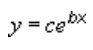
kur c un b ir konstantes un e ir naturālā logaritma bāze.
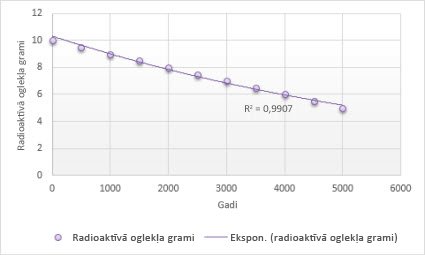
Tālāk redzamais eksponenciālās tendences līkne redzams objekta 14, kas samazinās ar tā vecumu. Ņemiet vērā, ka R kvadrāta vērtība ir 0,990, kas nozīmē, ka līnija datus precīzi ietilpinās.
Šī tendences līkne līdzina datu svārstības, lai skaidrāk parādītu modeli vai tendenci. Vidējais mainīgais izmanto noteiktu datu punktu skaitu (iestatīts ar opciju Periods), aprēķina to vidējo vērtību un izmanto vidējo vērtību kā punktu rindiņā. Piemēram, ja periodam ir iestatīta vērtība 2, pirmo divu datu punktu vidējā vērtība tiek izmantota kā vidējais mainīgais tendences līknes pirmais punkts. Otro un trešo datu punktu vidējā vērtība tiek izmantota kā tendenču līknes otrais punkts utt.
Kustīgas vidējās tendences līknē tiek izmantots šāds vienādojums:
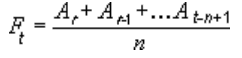
Punktu skaits vienā tendenču kustīgais vidējais ir vienāds ar sērijas punktu kopskaitu, mīnus periodā norādāt skaitli.
Izkaisītajā diagrammā tendenču līknes pamatā ir x vērtību secība diagrammā. Lai iegūtu labāku rezultātu, pirms vidējās vērtības pievienošanas sakārtojiet x vērtības.
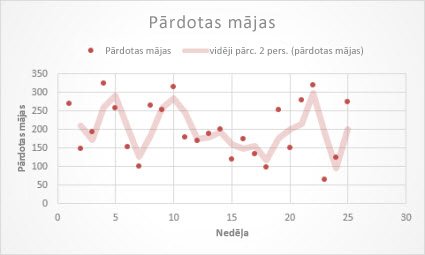
Tālāk redzamais vidējais mainīgais tendenču līkne parāda 26 nedēļu laikā pārdoto māju skaitu.
Svarīgi!: Sākot ar Excel versiju 2005, programma Excel pielāgoja R 2 vērtību lineārās tendences līknēm diagrammās, kur tendenču līknes krustpunkts ir iestatīts uz nulli (0). Šī korekcija izlabo aprēķinus, kas izlaboja nepareizas R2 vērtības, un līdzina R2 aprēķinus ar funkciju LINEST. Līdz ar to, iespējams, diagrammās, kas iepriekš izveidotas iepriekšējās Excel versijās, tiek rādītas atšķirīgas R 2 vērtības. Papildinformāciju skatiet rakstā Izmaiņas diagrammas lineārās tendenču līknes iekšējos aprēķinos.
Vai nepieciešama papildu palīdzība?
Vienmēr varat pajautāt speciālistam Excel tech kopienā vai saņemt atbalstu kopienās.
Skatiet arī
Tendences vai mainīgu vidējo vērtību līknes pievienošana diagrammai










