Šajā rakstā paskaidrota funkcijas RSQ funkciju programmā Microsoft Excel.
Apraksts
Atgriež Pīrsona korelācijas koeficienta kvadrātu norādītajos datu punktos zināmos_y un zināmos_x. Papildinformāciju skatiet rakstā Funkcija PEARSON. R-kvadrāta vērtību var interpretēt kā y dispersijas proporciju, piemērojot x dispersijai.
Sintakse
RSQ(zināmie_y,zināmie_x)
Funkcijas RSQ sintaksei ir šādi argumenti.
-
Zināmie_y Obligāts arguments. Datu punktu masīvs vai diapazons.
-
Zināmie_x Obligāts arguments. Datu punktu masīvs vai diapazons.
Piezīmes
-
Argumenti var būt skaitļi vai nosaukumi, masīvi vai atsauces, kas satur skaitļus.
-
Tiek skaitītas loģiskās vērtības un tekstuāls skaitļu atspoguļojums, kas ir ierakstīts tieši argumentu sarakstā.
-
Ja masīva vai atsauces arguments satur tekstu, loģiskas vērtības vai tukšas šūnas, šīs vērtības tiek ignorētas, taču šūnas ar nulles vērtību tiek iekļautas.
-
Argumenti, kas ir kļūdu vērtības vai teksts, ko nevar pārvērst par skaitļiem, izraisa kļūdas.
-
Ja zināmie_y un zināmie_x ir tukši vai tiem ir dažāds datu punktu skaits, funkcija RSQ atgriež kļūdas vērtību #N/A.
-
Ja known_y un known_x ir tikai 1 datu punkts, funkcija RSQ atgriež #DIV/0! kļūdas vērtību.
-
Vienādojums Pīrsona korelācijas koeficienta r noteikšanai ir:
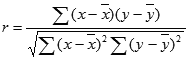
kur x un y ir parauga vidējās vērtības AVERAGE(zināmie_x) un AVERAGE(zināmie_y).
Funkcija RSQ atgriež r2, kas ir šī korelācijas koeficienta kvadrāts.
Piemērs
Nokopējiet šīs tabulas parauga datus un ielīmējiet tos jaunas Excel darblapas šūnā A1. Lai formulas parādītu rezultātus, atlasiet tos, nospiediet taustiņu F2 un pēc tam Enter. Ja nepieciešams, varat koriģēt kolonnas platumu, lai redzētu visus datus.
|
Dati |
||
|
Zināmais y |
Zināmais x |
|
|
2 |
6 |
|
|
3 |
5 |
|
|
9 |
11 |
|
|
1 |
7 |
|
|
8 |
5 |
|
|
7 |
4 |
|
|
5 |
4 |
|
|
Formula |
Apraksts |
R ezultāts |
|
=RSQ(A3:A9; B3:B9) |
Pīrsona korelācijas koeficienta kvadrāts diapazonā A3:A9 un B3:B9 norādītajiem datu punktiem |
0,05795 |










