Piezīme.: Mēs vēlamies sniegt jums visjaunāko palīdzības saturu jūsu valodā, cik vien ātri to varam. Šī lapa ir tulkota automatizēti, un tajā var būt gramatiskas kļūdas un neprecizitātes. Mūsu nolūks ir šo saturu padarīt jums noderīgu. Vai lapas lejasdaļā varat mums pavēstīt, vai informācija jums noderēja? Ērtai atsaucei šeit ir šis raksts angļu valodā.
Šajā rakstā skaidrots, kā izmantot pievienojumprogrammu Risinātājs — Microsoft Excel pievienojumprogrammu, ko varat izmantot iespēju analīzē, lai noteiktu optimālu produktu kombināciju.
Kā varu noteikt mēneša produktu sortimentu, kas palielina rentabilitāti?
Uzņēmumiem bieži ir jānosaka katra produkta daudzums, kas jāsaražo ik mēnesi. Vienkāršākajā veidā produkta Miksētā problēma ir saistīta ar to, kā noteikt katra produkta daudzumu, kas jāražo mēneša laikā, lai palielinātu peļņu. Produktu sortimentam parasti jāatbilst šādiem ierobežojumiem:
-
Produktu sortimentā nevar izmantot vairāk resursu, nekā ir pieejams.
-
Katram produktam ir ierobežots pieprasījums. Mēneša laikā nav iespējams saražot vairāk produktu, jo tiek diktēts liekais ražošanas apjoms (piemēram, ātrbojīgas narkotikas).
Tagad atrisinās šo produkta miksētās problēmas piemēru. Šī risinājuma risinājumu varat atrast failā Prodmix. xlsx, kas redzams 27-1 attēlā.
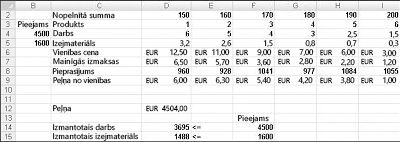
Pieņemsim, ka mēs strādājam pie narkotiku kompānijas, kas savā uzņēmumā ražo sešus dažādus produktus. Katra produkta ražošanai ir nepieciešams darbaspēks un izejmateriāls. 4. rindā attēlā 27-1 ir redzams darba laiks, kas nepieciešams, lai izveidotu mārciņu katram produktam, un 5. rindā ir redzamas mārciņas no izejmateriāla, kas ir nepieciešams, lai izveidotu mārciņas katram produktam. Piemēram, ja tiek ražota produkta 1 mārciņa, nepieciešamas sešas darba stundas un 3,2 mārciņas izejmateriāla. Katrai narkotikai katras mārciņas cena ir norādīta 6. rindā, vienības pašizmaksa vienā mārciņā ir norādīta 7. rindā, un peļņas daļa GBP ir norādīta 9. rindā. Piemēram, produktu 2 pārdod par $11,00 uz mārciņu, rodas vienības izmaksas $5,70 par mārciņu un veicina $5,30 peļņu mārciņā. Mēneša pieprasījums katram narkotiku ir dots 8. rindā. Piemēram, pieprasījums pēc produkta 3 ir 1041 mārciņas. Šajā mēnesī 4500 stundas darba un 1600 mārciņas izejmateriālu ir pieejamas. Kā šis uzņēmums var maksimizēt mēneša peļņu?
Ja mēs neko nezinājām par Excel Solver, šī problēma ir uzlikta, izveidojot darblapu, lai sekotu peļņas un resursu lietojumam, kas saistīti ar šo produktu kombināciju. Pēc tam mēs izmantosim izmēģināšanu un kļūdu, lai dažādotu produktu sortimentu un optimizētu peļņu, neizmantojot vairāk darba vai izejmateriālu, nekā ir pieejams, un neveidojot narkotiku, kas pārsniedz pieprasījumu. Šajā procesā ir jāizmanto Risinātājs tikai izmēģinājuma un kļūdu posmā. Būtībā Risinātājs ir optimizācijas dzinējs, kas nevainojami veic izmēģinājumversiju un kļūdu meklēšanu.
Atslēgu, lai atrisinātu produktu miksētās problēmas, ir efektīvi aprēķināt resursu lietojumu un peļņu, kas saistīta ar attiecīgo produktu kombināciju. Svarīgs rīks, ko var izmantot, lai veiktu šo aprēķinu, ir funkcija SUMPRODUCT. Funkcija SUMPRODUCT reizina atbilstošās vērtības šūnu diapazonos un atgriež šo vērtību summu. SUMPRODUCT novērtējumā izmantotajiem šūnu diapazoniem ir jābūt tiem pašiem izmēriem, kas norāda, ka varat izmantot SUMPRODUCT ar divām rindām vai divām kolonnām, bet ne ar vienu kolonnu un vienu rindu.
Kā piemēru par to, kā mēs varam izmantot funkciju SUMPRODUCT mūsu produktu mix piemērā, mēģināsim aprēķināt mūsu resursu lietojumu. Mūsu darba lietojumu aprēķina
(Darba lietojums uz vienu mārciņu narkotiku 1) * (preparāts 1 mārciņas) + (darba izmantotais per Pound of Drug 2) * (narkotiku 2 mārciņas) +... (Darba lietojums uz vienu mārciņu narkotiku 6) * (saražots narkotiku 6 mārciņas)
Mēs varam aprēķināt darba izmantošanu daudz apnicīgā veidā, jo D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + diapazonā I2 * I4. Tāpat izejmateriālu izmantošanu var aprēķināt kā D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + diapazonā I2 * i5. Tomēr, ievadot šīs formulas darblapā, sešiem produktiem ir laikietilpīgs. Iedomājieties, cik ilgs laiks būtu nepieciešams, ja strādātu ar uzņēmumu, kas ražoja, piemēram, 50 produktus savā uzņēmumā. Daudz vienkāršāks veids, kā aprēķināt darba un izejmateriālu lietojumu, ir kopēt no D14 uz D15 formulu SUMPRODUCT ($D $2: $I $2, D4: I4). Šajā formulā tiek aprēķināts D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + diapazonā I2 * I4 (kas ir mūsu darba lietojums), bet ir daudz vienkāršāk ievadīt! Ņemiet vērā, ka es izmantoju $ zīmi ar diapazonu D2: diapazonā I2, lai, Kopējot formulu, joprojām tvert produktu sortimentu no 2. rindas. Formula šūnā D15 aprēķina izejmateriālu lietojumu.
Līdzīgā veidā mūsu peļņu nosaka
(1. preparāta peļņa uz mārciņu) * (preparāts, 1 mārciņas) + (2. gada peļņa par mārciņu) * (2. gada 4 mārciņas) +... (Narkotiku 6 peļņa uz mārciņu) * (saražota narkotiku 6 mārciņas)
Peļņa ir viegli izskaitļota šūnā D12 ar formulu SUMPRODUCT (D9: I9, $D $2: $I $2).
Tagad mēs varam noteikt mūsu produktu mix Solver modeļa trīs komponentus.
-
Mērķis šūnu.Mūsu mērķis ir maksimizēt peļņu (izskaitļots šūnā D12).
-
Mainiet šūnas.Katra produkta saražoto mārciņas skaits (norādīts šūnu diapazonā D2: diapazonā I2)
-
Ierobežojumiem. Mums ir šādi ierobežojumi:
-
Neizmantojiet vairāk darba vai izejmateriālu, nekā ir pieejams. Tas nozīmē, ka šūnās D14: D15 (izmantotajos resursos) ir jābūt mazākam vai vienādam ar vērtībām šūnās F14: F15 (pieejamie resursi).
-
Neražojiet vairāk narkotiku, nekā ir pieprasīts. Tas nozīmē, ka vērtībām šūnās D2: diapazonā I2 (katras narkotikas saražotās mārciņas) ir jābūt mazākam vai vienādam ar katras narkotikas pieprasījumu (norādīts šūnās D8: i8).
-
Mēs nevaram izveidot negatīvu summu no jebkuras narkotikas.
-
Es parādīšu, kā ievadīt mērķis šūnu, mainot šūnas un ierobežojumus pievienojumprogrammā risinātājs. Pēc tam jānoklikšķina uz pogas atrisināt, lai atrastu peļņas palielināšanas produktu sortimentu!
Lai sāktu darbu, noklikšķiniet uz cilnes dati un grupā Analīze noklikšķiniet uz Risinātājs.
Piezīme.: Kā paskaidrots nodaļā 26, "Ievads par optimizāciju ar Excel Solver", Risinātājs tiek instalēts, noklikšķinot uz Microsoft Office pogas, pēc tam uz Excel opcijas un pēc tam uz pievienojumprogrammas. Sarakstā pārvaldīt noklikšķiniet uz Excel pievienojumprogrammas, atzīmējiet rūtiņu Risinātāja pievienojumprogramma un pēc tam noklikšķiniet uz Labi.
Tiks parādīts dialoglodziņš Risinātāja parametri, kā parādīts 27-2 attēlā.
Noklikšķiniet uz lodziņa iestatīt mērķi šūnā un pēc tam atlasiet mūsu peļņas šūnu (šūna D12). Noklikšķiniet uz lodziņa pēc mainīgo šūnu un pēc tam norādiet uz diapazonu D2: diapazonā I2, kurā ir katras narkotikas saražotās mārciņas. Tagad dialoglodziņam ir jāizskatās skaitlim 27-3.
Tagad esam gatavi pievienot šim modelim ierobežojumus. Noklikšķiniet uz pogas Pievienot. Tiks parādīts dialoglodziņš CONSTRAINT pievienošana, kas parādīts attēlā 27-4.
Lai pievienotu resursu lietojuma ierobežojumus, noklikšķiniet uz šūnas atsauces lodziņa un pēc tam atlasiet diapazonu D14: D15. Sarakstā vidējais atlasiet < =. Noklikšķiniet uz lodziņa CONSTRAINT un pēc tam atlasiet šūnu diapazonu F14: F15. Dialoglodziņš CONSTRAINT pievienošana tagad ir jāizskatās kā 27-5 attēls.
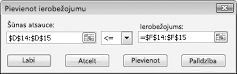
Tagad ir nodrošināts, ka, ja Risinātājs mēģina dažādas vērtības mainīgajām šūnām, tikai tās kombinācijas, kas atbilst gan D14< = F14 (darba lietojums ir mazāks vai vienāds ar darbaspēku) un D15< = F15 (izmantotais izejmateriāls ir mazāks vai vienāds ar izejmateriāls ir pieejams). Lai ievadītu pieprasījuma ierobežojumus, noklikšķiniet uz Pievienot. Aizpildiet dialoglodziņu CONSTRAINT pievienošana, kā parādīts 27-6 attēlā.
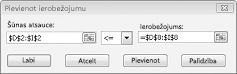
Pievienojot šos ierobežojumus, tiek nodrošināts, ka Risinātājam ir dažādas šūnu vērtību kombinācijas, kas atbilst tālāk norādītajiem parametriem.
-
D2< = D8 (1. preparāts ir mazāks par vai vienāds ar 1. narkotiku pieprasījuma apjomu)
-
E2< = E8 (saražotās narkotikas lielums ir mazāks vai vienāds ar 2. narkotiku pieprasījumu)
-
F2< = F8 (saražotais narkotiku 3 lielums ir mazāks vai vienāds ar narkotiku pieprasījumu 3)
-
G2< = G8 (saražotais narkotiku 4 lielums ir mazāks vai vienāds ar narkotiku pieprasījumu 4)
-
H2< = H8 (par narkotiku 5, kas iegūts, ir mazāks vai vienāds ar narkotiku pieprasījumu 5)
-
I2< = I8 (saražotais narkotiku 6 lielums ir mazāks vai vienāds ar narkotiku pieprasījumu 6)
Dialoglodziņā CONSTRAINT pievienošana noklikšķiniet uz Labi. Risinātāja logam ir jāizskatās kā 27-7.
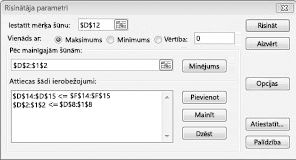
Dialoglodziņā Risinātāja opcijas ir jāievada ierobežojums, kas maina šūnu vērtības. Dialoglodziņā Risinātāja parametri noklikšķiniet uz pogas opcijas. Atzīmējiet izvēles rūtiņu Assume Linear Model un uzŅemt neNegatīvos lodziņu, kā parādīts nākamajā lappusē, 27-8 attēls. Noklikšķiniet uz Labi.
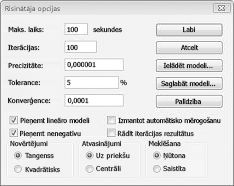
PārBaudot, vai neNegatīvs lodziņš nodrošina to, ka Risinātājam ir tikai mainīgu šūnu kombinācijas, kurās katrai mainīgajai šūnai tiek pieņemta vērtība, kas nav negatīva. Mēs atzīmējām lodziņu Assume Linear Model, jo produkta mix problēma ir īpaša tipa risinātāja problēma, kas tiek dēvēta par lineāru modeli. Būtībā risinātāja modelis ir lineārs, ievērojot šādus nosacījumus:
-
Mērķis šūnā tiek aprēķināts, saskaitot kopā formas nosacījumus (mainot šūnu) * (konstante).
-
Katrs ierobežojums atbilst "lineārā modeļa prasībām". Tas nozīmē, ka katru ierobežojumu novērtē, saskaitot kopā formas noteikumus (mainīgo šūnu) * (konstante) un salīdzinot summas ar konstanti.
Kāpēc šī Risinātāja problēmu lineāra? Mūsu mērķis (peļņa) tiek aprēķināts kā
(1. preparāta peļņa uz mārciņu) * (preparāts, 1 mārciņas) + (2. gada peļņa par mārciņu) * (2. gada 4 mārciņas) +... (Narkotiku 6 peļņa uz mārciņu) * (saražota narkotiku 6 mārciņas)
Šajā aprēķinā ir parādīts raksts, kurā mērķa šūnas vērtība ir iegūta, saskaitot kopā formas noteikumus (mainot šūnu) * (konstante).
Mūsu darba ierobežojums tiek novērtēts, salīdzinot vērtību, kas iegūta no (darba lietojums uz vienu mārciņu no narkotiku 1) * (narkotiku 1 mārciņas ražots) + (darba izmanto per Pound of Drug 2) * (narkotiku 2 mārciņas) +... (Darbs ar mumsEd per Pound of Drug 6) * (saražotĀs narkotikas 6 mārciņas) uz pieejamo darbu.
Tādējādi darba ierobežojums tiek novērtēts, saskaitot formas nosacījumus (mainot šūnu) * (konstante) un salīdzinot summas ar konstanti. Gan darba ierobežojums, gan izejmateriālu ierobežojums atbilst lineārā modeļa prasībām.
Mūsu pieprasījuma ierobežojumi atbilst formai
(Preparāts 1 ražots) < = (narkotiku 1 pieprasījums) (2. preparāts) < = (narkotiku 2 pieprasījums) § (saražotais narkotiku 6) < = (narkotiku 6 pieprasījums)
Katrs pieprasījuma ierobežojums atbilst lineārā modeļa prasībai, jo katru no tiem novērtē, saskaitot kopā formas noteikumus (mainot šūnu) * (konstante) un salīdzinot summas ar konstanti.
Ja ir redzams, ka mūsu produktu sortimenta modelis ir lineārs modelis, kāpēc mums būtu jārūpējas?
-
Ja risinātāja modelis ir lineārs un mēs atlasāt pieņemt lineāru modeli, Risinātājam ir garantēts optimālākais risinājums risinātāja modelim. Ja risinātāja modelis nav lineārs, Risinātājs var neatrast optimālo risinājumu.
-
Ja risinātāja modelis ir lineārs un mēs atlasāt Assume Linear Model, Risinātājs izmanto ļoti efektīvu algoritmu (simplex metodi), lai atrastu modeļa optimālo risinājumu. Ja risinātāja modelis ir lineārs un netiek atlasīts Pieņemt lineāru modeli, Risinātājs izmanto ļoti neefektīvu algoritmu (GRG2 metodi), un, iespējams, ir grūti atrast modeļa optimālo risinājumu.
Kad dialoglodziņā Risinātāja opcijas ir noklikšķinājis uz Labi, atgriežaties pie galvenā risinātāja dialoglodziņa, kas parādīts iepriekš attēlā 27-7. Kad noklikšķināt uz atrisināt, Risinātājs aprēķina optimālu risinājumu (ja tāds ir) mūsu produktu mix modelim. Kā es norādīju nodaļā 26, optimālais produktu sortimenta modeļa risinājums ir šūnu vērtību (mārciņas, kas ražotas no katras narkotikas) kopa, kas palielina peļņu, izmantojot visu iespējamo risinājumu kopu. Atkal iespējamais risinājums ir mainīgu šūnu vērtību kopa, kas atbilst visiem ierobežojumiem. Mainīgajām šūnu vērtībām, kas redzamas attēlā 27-9, ir iespējamais risinājums, jo visi ražošanas līmeņi ir nenegatīvi, ražošanas līmeņi nepārsniedz pieprasījumu, un resursu lietojums nepārsniedz pieejamos resursus.
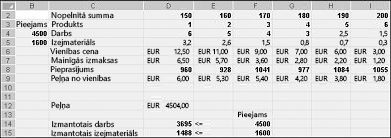
Mainīgajām šūnu vērtībām, kas tiek rādītas 27-10 attēlā nākamajā lappusē, ir neizpildāms risinājums šādu iemeslu dēļ:
-
Mēs ražojam vairāk narkotiku 5, nekā to prasa.
-
Mēs izmantojam vairāk darba, nekā ir pieejams.
-
Mēs izmantojam papildu izejmateriālus, nekā ir pieejams.
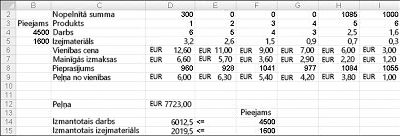
Pēc tam, kad noklikšķināt uz risināt, Risinātājs ātri atrod optimālo risinājumu, kas redzams 27-11 attēlā. Lai darblapā saglabātu optimālās risinājuma vērtības, ir jāatlasa Saglabāt Risinātāja risinājumu.
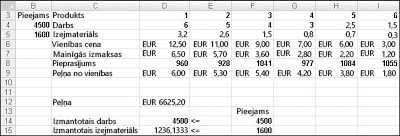
Mūsu narkotiku uzņēmums var maksimizēt savu mēneša peļņu $6 625,20, uzrādot 596,67 mārciņas narkotiku 4, 1084 mārciņas narkotiku 5, un neviens no pārējiem narkotiku! Mēs nevaram noteikt, vai mēs varam sasniegt $6 625,20 maksimālo peļņu citos veidos. Mēs varam būt pārliecināti par to, ka mūsu ierobežotie resursi un pieprasījums nav iespējams veikt vairāk nekā $6 627,20 šajā mēnesī.
Pieņemsim, ka katram produktam ir jāizpilda pieprasījums. (Failā Prodmix. xlsx) nav atrodama neviena iespējamā risinājumu darblapa. Pēc tam mums būs jāmaina mūsu pieprasījuma ierobežojumi no D2: I2< = D8: i8 uz D2: I2> = D8: i8. Lai to izdarītu, atveriet pievienojumprogrammu Risinātājs, atlasiet D2: I2< = D8: i8 CONSTRAINT un pēc tam noklikšķiniet uz mainīt. Tiek atvērts dialoglodziņš mainīt ierobežojumu, kas redzams 27-12 attēlā.
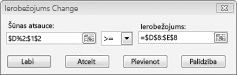
Atlasiet > = un pēc tam noklikšķiniet uz Labi. Tagad esam nodrošinājuši, ka Risinātājs apsvērs iespēju mainīt tikai šūnu vērtības, kas atbilst visām prasībām. Noklikšķinot uz atrisināt, parādās ziņojums "risinātājs nevarēja atrast izpildāmu risinājumu." Šis ziņojums nenozīmē, ka mūsu modelī esam pieļāvuši kļūdu, bet gan to, ka mūsu ierobežotie resursi nevar apmierināt pieprasījumu pēc visiem produktiem. Risinātājam ir vienkārši norādīts, ka, ja mēs vēlamies apmierināt katra produkta pieprasījumu, mums ir jāpievieno vairāk darba, vairāk izejmateriālu vai vairāk.
Redzēsim, kas notiek, ja mēs ļaujam katram produktam neierobežotu pieprasījumu, un mēs atļaujam no katras narkotikas ražot negatīvus daudzumus. (Izmantojot šo Risinātāja problēmu, iestatītĀs vērtības nekonverģē darblapā failu Prodmix. xlsx.) Lai atrastu šo situāciju optimālo risinājumu, atveriet pievienojumprogrammu Risinātājs, noklikšķiniet uz pogas opcijas un notīriet izvēles rūtiņu pieņemt neNegatīvos. Dialoglodziņā Risinātāja parametri atlasiet ierobežojumu pieprasījuma D2: I2< = D8: i8 un pēc tam noklikšķiniet uz Dzēst, lai noņemtu ierobežojumu. Noklikšķinot uz atrisināt, Risinātājs atgriež ziņojumu "šūnu vērtību iestatīšana nesaPlūst". Šis ziņojums nozīmē, ka, ja mērķis ir maksimizēts (kā mūsu piemērā), ir iespējami risinājumi ar patvaļīgi lielām šūnu vērtībām. (Ja mērķis ir minimizēt, ziņojums "šūnu vērtību iestatīšana neKonverģē" nozīmē, ka ir iespējami risinājumi ar patvaļīgi mazām šūnu vērtībām.) Mūsu situācijā, atļaujot nelabvēlīgu narkotiku ražošanu, mēs esam spēkā "izveidot" resursus, ko var izmantot, lai izveidotu patvaļīgi daudz citu narkotiku. Ņemot vērā mūsu neierobežoto pieprasījumu, tas ļauj mums veikt neierobežotu peļņu. Reālajā situācijā mēs nevaram padarīt neierobežotas naudas summas. Īsumā, ja redzat "Set Values not konverģē", jūsu modelim ir kļūda.
-
Pieņemsim, ka mūsu narkotiku uzņēmums var iegādāties līdz pat 500 darba laiku par $1 vairāk stundā par pašreizējām darbaspēka izmaksām. Kā var palielināt peļņu?
-
Pie mikroshēmas ražotne, četri tehniķi (A, B, C un D) izveido trīs produktus (produkti 1, 2 un 3). Šajā mēnesī mikroshēmu ražotājs var pārdot 80 produktu 1, 50 vienību produktu 2 un lielāko daļu 50 vienību 3. Tehniķis A var veikt tikai produktus 1 un 3. Tehniķis B var veikt tikai 1. un 2. produktu. Tehniķis C var veikt tikai produktu 3. Tehniķis D var veikt tikai produktu 2. Katrai saražotajai vienībai produkti veicina šādu peļņu: product 1, $6; Produkts 2, $7; and Product 3, $10. Laiks (stundās) katram tehniķim ir jāražo produkts, ir šāds:
Produkts
Tehniķis A
Tehniķis B
Tehniķis C
Tehniķis D
1
2
2,5
Nevar veikt
Nevar veikt
2
Nevar veikt
3
Nevar veikt
3,5
3
3
Nevar veikt
4
Nevar veikt
-
Katrs tehniķis var strādāt līdz 120 stundām mēnesī. Kā mikroshēmu ražotājs var maksimizēt mēneša peļņu? Pieņemiet, ka ir iespējams saražot dalītu vienību skaitu.
-
Datora ražošanas uzņēmums izveido peles, tastatūras un video spēļu kursorsviras. Katrai vienības peļņai, katrai vienībai paredzētā darba samaksa, mēneša pieprasījums un vienas vienības datora lietošanas laiks ir norādīts tālāk esošajā tabulā.
Pelēm
Tastatūras
Kursorsviras
Peļņa/vienība
$8
$11
$9
Darba lietojums/vienība
.2 stunda
.3 stunda
.24 stunda
Datora laiks/ierīce
.04 stunda
.055 stunda
.04 stunda
Mēneša pieprasījums
15 000
27 000
11 000
-
Katru mēnesi kopā ir pieejami 13 000 darba laika un 3000 stundu datora laiks. Kā ražotājs var maksimizēt savas mēneša peļņas iemaksas no rūpnīcas?
-
AtRisiniet mūsu narkotiku piemēru, pieņemot, ka ir jāizpilda minimālā prasība par 200 vienībām katrai narkotikai.
-
Jason izveido dimanta aproces, kaklarotas un auskarus. Viņš vēlas strādāt ne vairāk kā 160 stundas mēnesī. Viņam ir 800 unces dimantu. Tālāk ir norādītas to dimantu peļņa, darba laiks un unces, kas nepieciešami, lai ražotu katru produktu. Ja pieprasījums katram produktam ir neierobežots, kā Jason var palielināt peļņu?
Produkts
Vienības peļņa
Darba laiks uz vienību
Unces ar dimantiem uz vienību
Rokassprādze
300 €
.35
1.2
Kaklarota
200 €
.15
.75
Auskari
100 €
0.05
0,5










