Risinātāja izmantošana kapitālieguldījumu budžetam

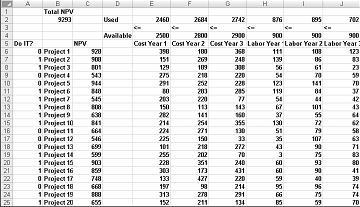
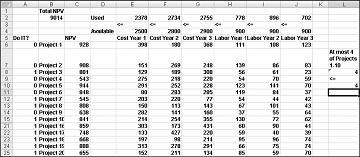
Lielākā daļa uzņēmumu vēlas veikt projektus, kuri veicina lielāko pašreizējo neto vērtību (NPV), ir pakļauta ierobežotam resursu skaitam (parasti galvaspilsēta un korporācija). Pieņemsim, ka programmatūras izstrādes uzņēmums mēģina noteikt, kuri no 20 programmatūras projektiem tam jāveic. Katra projekta NPV (miljoniem dolāru), kā arī galvaspilsēta (miljoniem dolāru) un programmētāju skaits, kas nepieciešams nākamo trīs gadu laikā, ir norādīts faila Capbudget.xlsx darblapā Pamata modelis, kas redzams nākamajā lapā attēlā 30-1. Piemēram, Project 2 dod 908 miljonu dolāru. 1. gadā tai ir nepieciešami 151 miljoni EUR 269 miljoni 2. gadā, bet 248 miljoni — 3. gadā. 2. projektam nepieciešami 139 programmētāji 1. gadā, 86 programmētāji 2. gadā un 83 programmētāji 3. gadā. Šūnās E4:G4 redzams katram no trim gadiem pieejamais galvaspilsētas (miljoniem dolāru), bet šūnā H4:J4 ir norādīts, cik programmētāju ir pieejams. Piemēram, 1. gadā ir pieejami līdz pat 2,5 miljoniem dolāru lielajiem un 900 programmētājiem.

Uzņēmumam ir jāizlemj, vai tam jāizvērtē katrs projekts. Pieņemsim, ka nevaram veikt programmatūras projekta daļu; ja mēs, piemēram, iedalītu 0,5 no nepieciešamajiem resursiem, mums būtu bezpeļņas programma, kas mums nodrošinātu 0 $ ieņēmumus!

Lai modelējot lietotu binārās izmaiņas, ir jāizmanto binārās izmaiņas. Binārā mainīgajā šūnā vienmēr ir vienāds ar 0 vai 1. Ja binārā mainīgajā šūnā, kas atbilst projektam, ir vienāds ar 1, tiek izdarīts šis projekts. Ja binārā mainīgajā šūnā, kas atbilst projektam, ir vienāda ar 0, projekts netiek paveikts. Risinātāju var iestatīt bināro izmaiņu šūnu diapazona izmantošanai, pievienojot ierobežojumu — atlasiet maināmās šūnas, kuras vēlaties izmantot, un pēc tam dialoglodziņa Ierobežojuma pievienošana sarakstā izvēlieties Bin.

Ar šo fonu esam gatavi risināt programmatūras projekta atlases problēmu. Kā vienmēr, izmantojot risinātāja modeli, mēs sākam identificēt mērķa šūnu, mainīgās šūnas un ierobežojumus.

• Mērķa šūna. Mēs maksimizēt atlasīto projektu ģenerēto NPV.

• Tiek mainītas šūnas. Mēs meklēsim 0 vai 1 bināro izmaiņu šūnu katram projektam. Esmu atradis šīs šūnas diapazonā A6:A25 (un diapazona doit). Piemēram, 1 šūnā A6 norāda, ka mēs veiksim Project 1; 0 šūnā C6 norāda, ka project 1 nav nepieciešams.

• Ierobežojumus. Mums ir jānodrošina, ka katram gadam t (t=1, 2, 3), izmantotais gads t ir mazāks vai vienāds ar pieejamo gada t lielo burtu un izmantotais Gads t t ir mazāks vai vienāds ar Pieejamo gada t burtu.

Kā redzams, mūsu darblapā ir skaitļojiet NPV projektu atlasei, katru gadu izmantotajiem kapitālieguldījumu klientiem un programmētājiem. Šūnā B2 izmantoju formulu SUMPRODUCT(doit,NPV ), lai aprēķinātu kopējo atlasīto projektu ģenerēto NPV. (Diapazona nosaukums NPV atsaucas uz diapazonu C6:C25.) Katram projektam, kuru kolonnā A ir 1, šī formula paņem projekta NPV, bet katram projektam kolonnā A ir vērtība 0, šī formula neaņem projekta NPV. Tāpēc ir iespējams aprēķināt visu projektu NPV, un mūsu mērķa šūna ir lineāra, jo to aprēķina, summējot pēc formas esošos terminus (mainot šūnu)*(konstante). Līdzīgā veidā es izskaitļoju katru gadu izmantoto galvaspilsētu un katru gadu lietoto lielo burtu, kopējot no E2 līdz F2:J2 formulai SUMPRODUCT(doit,E6:E25).

Tagad aizpildu dialoglodziņu Risinātāja parametri, kā parādīts attēlā 30-2.

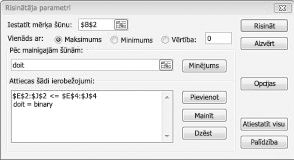
Mūsu mērķis ir maksimāli palielināt atlasīto projektu NPV (šūna B2). Mūsu mainīgās šūnas (diapazons ar nosaukumu doit) ir katra projekta binārās maiņas šūnas. Ierobežojums E2:J2<=E4:J4 nodrošina, ka katra gada laikā izmantotais lielais un dāsns ir mazāks vai vienāds ar lielo burtu un kolonnas. Lai pievienotu ierobežojumu, kas maina šūnu bināro vērtību, dialoglodziņā Risinātāja parametri noklikšķiniet uz Pievienot un dialoglodziņa vidū parādītajā sarakstā atlasiet Bin. Dialoglodziņš Pievienot ierobežojumu tiek parādīts, kā parādīts attēlā 30-3.

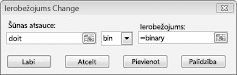
Mūsu modelis ir lineārs, jo mērķa šūna tiek aprēķināta kā nosacījumu summa, kas satur formu (mainīga šūna )*( konstante), un tāpēc, ka resursu lietojuma ierobežojumi tiek aprēķināti, salīdzinot (mainot šūnas )*( konstantes) summu ar konstanti.

Kad dialoglodziņš Risinātāja parametri ir aizpildīts, noklikšķiniet uz Risināt, un rezultāti tiks rādīti iepriekš attēlā 30-1. Uzņēmums var iegūt maksimālo NPV 9293 miljonu (9,293 EUR miljardi) apmērā, izvēloties Projektus 2, 3, 6–10, 14–16, 19 un 20.

Dažkārt projekta atlases modeļiem ir citi ierobežojumi. Piemēram, ja atlasām Project 3, ir jāatlasa arī Project 4. Tā kā mūsu pašreizējais optimālais risinājums atlasa Project 3, bet ne Project 4, mēs zinām, ka mūsu pašreizējais risinājums nepaliek optimāls. Lai novērstu šo problēmu, vienkārši pievienojiet ierobežojumu, ka Binārā izmaiņu šūna programmā Project 3 ir mazāka vai vienāda ar bināro izmaiņu šūnu programmā Project 4.

Šo piemēru varat atrast faila darblapas darblapā Ja 3 un 4 Capbudget.xlsx, kas redzams attēlā 30–4. Šūna L9 attiecas uz bināro vērtību, kas saistīta ar Project 3, un šūnu L12 ar bināro vērtību, kas saistīta ar Project 4. Pievienojot ierobežojumu L9 vai<=L12, ja izvēlaties Project 3, L9 ir vienāds ar 1 un mūsu ierobežojumam L12 (Project 4 binārais) ir vienāds ar 1. Ja neatlasām Project 3, mūsu ierobežojumam ir jāatstāj arī binārā vērtība mainīgajā Project 4 šūnā. Ja neatlasot Project 3, L9 ir vienāds ar 0 un mūsu ierobežojums ļauj Project 4 binārajam skaitlim vienāds ar 0 vai 1, kas ir tas, ko mēs vēlamies. Jaunais optimālais risinājums tiek parādīts 30.–4. attēlā.

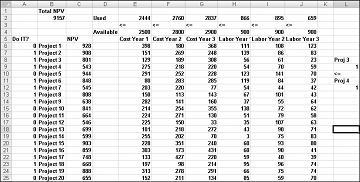
Jauns optimāls risinājums tiek aprēķināts, ja atlasāt Project 3, mums ir jāatlasa arī Project 4. Tagad pieņemsim, ka no 1. līdz 10. projektam varam veikt tikai četrus projektus. (Skatiet darblapu Vismaz 4 no P1–P10 , kas parādīta attēlā 30-5.) Šūnā L8 tiek aprēķināta ar projektiem no 1 līdz 10 saistīto bināro vērtību summa ar formulu SUM(A6:A15). Pēc tam mēs pievienojam ierobežojumu L8<=L10, kas nodrošina, ka tiek atlasīti vismaz 4 no pirmajiem 10 projektiem. Jaunais optimālais risinājums tiek parādīts 30.–5. attēlā. NPV ir nomests uz 9,014 EUR miljardi.

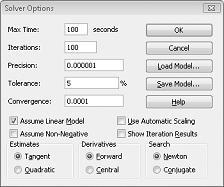
Lineārā risinātāja modeļi, kuros dažām vai visām mainīgajām šūnām ir jābūt binārajam vai veselam skaitlim, parasti ir grūtāk risināt nekā lineāri modeļi, kuros visas mainīgajās šūnas drīkst būt daļskaitļi. Šī iemesla dēļ esam apmierināti ar optimālu binārā vai vesela skaitļa programmēšanas problēmu. Ja risinātāja modelis darbojas ilgu laiku, iespējams, vēlēsities pielāgot iestatījumu Pielaide dialoglodziņā Risinātāja opcijas. (Skatiet attēlu 30-6.) Piemēram, iestatījums Pielaide 0,5% nozīmē, ka risinātājs pārtrauks pirmo reizi, kad atrod iespējamu risinājumu, kas ir 0,5 procentus no optimālās mērķa šūnas vērtības (optimālā mērķa šūnas vērtība ir optimālā mērķa vērtība, kas tiek atrasta, ja izlaisti binārie un veselo skaitļu ierobežojumi). Bieži vien mums ir grūti izvēlēties atrast atbildi 10 procentu laikā no optimālas 10 minūšu laikā vai atrast optimālu risinājumu divu nedēļu laikā pēc datora laika! Noklusējuma pielaides vērtība ir 0,05%, kas nozīmē, ka risinātājs pārstāj darboties, kad atrod mērķa šūnas vērtību, kas atbilst 0,05 procentiem no optimālās mērķa šūnas vērtības.

1. Uzņēmumā tiek izskatīti deviņi projekti. NPV, kas pievienots katram projektam, un katram projektam nepieciešamais galvaspilsēta nākamo divu gadu laikā ir redzams tālāk esošajā tabulā. (Visi skaitļi ir miljoniem.) Piemēram, Project 1 NPV pievienos 14 miljonuSV un pieprasa 12 miljonu lielus izdevumus 12 miljonu apmērā 1. gadā un 3 miljonu $ 2. gadā. 1. gadā projektiem ir pieejami 50 miljoni EUR, bet 2. gadā ir pieejami 20 miljoni EUR.

	NPV	1. gada izdevumi	2. gada izdevumi
Project 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	12	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Ja nevaram uzņemt nelielu projekta daļu, bet ir jāveic tikai viss projekts vai kāds cits projekts, kā mēs varam maksimizēt NPV?

• Pieņemsim, ka, ja Project 4 tiek veikta, ir jāveic Project 5. Kā mēs varam maksimizēt NPV?

• Publicēšanas uzņēmums mēģina noteikt, kuras no 36 grāmatām publicēt šogad. Failu Pressdata.xlsx sniegta šāda informācija par katru grāmatu:

  • Prognozētās ieņēmumu un izstrādes izmaksas (tūkstošos dolāru)

  • Pages in each book

  • Vai grāmata ir nolikta programmatūras izstrādātāju auditorijai (kolonnā E to norāda 1)

    Publicējot uzņēmumu, šogad var publicēt grāmatas ar kopsummu līdz 8500 lapām, kā arī publicēt vismaz četras grāmatas no programmatūras izstrādātājiem. Kā uzņēmums var maksimizēt savu peļņu?

Šis raksts ir adaptēts no Wayne L. Winston programmas Microsoft Office Excel 2007 datu analīzes un biznesa modelēšanas.

Šo klases stilu grāmatu ir izstrādājusi Wayne Winston, labi zināma statistiska un biznesa profesore, kas specializējas radošās un praktiskajās Excel lietojumprogrammās.