Analīzes rīku komplekta izmantošana salikto datu analīzes vajadzībām

1. Noklikšķiniet uz cilnes Fails, Opcijas un pēc tam uz kategorijas Pievienojumprogrammas.

2. Lodziņā Pārvaldīt atlasiet Excel pievienojumprogrammas un pēc tam noklikšķiniet uz Doties uz.

   Ja izmantojat programmu Excel darbam ar Mac, failu izvēlnē atveriet sadaļu Rīki >Excel pievienojumprogrammas.

3. Lodziņā Pievienojumprogrammas atzīmējiet izvēles rūtiņu Analīzes rīku komplekts un pēc tam noklikšķiniet uz Labi.

   • Ja lodziņā Pieejamās pievienojumprogrammas nav norādīta opcija Analīzes rīku komplekts, noklikšķiniet uz Pārlūkot, lai to atrastu.

   • Ja tiek parādīta uzvedne, kas informē par to, ka analīzes rīku komplekts nav instalēts datorā, noklikšķiniet uz Jā, lai to instalētu.

Anova analīzes rīki piedāvā dažādus dispersijas analīzes tipus. Izmantojamie rīki ir atkarīgi no daudziem faktoriem un paraugu skaita, kurus ieguvis no populācijas, kuru vēlaties testēt.

Anova: vienfaktors

Šis rīks veic vienkāršu datu dispersijas analīzi diviem vai vairāk paraugiem. Analīze sniedz hipotēzes testu, ka katrs paraugs tiek izvilkts no tās pašas pamatā esošās varbūtības sadalījuma attiecībā pret alternatīvu hipotēzes, ka pamatā esošā varbūtības sadale nav vienāda visām izlasēm. Ja ir tikai divi paraugi, varat izmantot darblapas funkciju T.PĀRBAUDĪT. Vairāk nekā divos paraugos nav ērtaS T vispārināšanas.TEST, un tā vietā var izsaukt vienfaktors Anova modeli.

Anova: divfaktors ar replicēšanu

Šis analīzes rīks ir noderīgs, kad datus var klasificēt divās dažādās dimensijās. Piemēram, augu garumu mērīšanas eksperimentā augiem var dot dažādu veidu mēslojumu (piemēram, A, B, C) un tos var turēt arī dažādās temperatūrās (piemēram, zemā, augstā). Katram no sešiem iespējamiem pāriem {mēslojums, temperatūra} ir vienāds augu garuma novērojumu skaits. Izmantojot šo Anova rīku, var pārbaudīt:

• Vai augu garumi dažādu veidu mēslojumiem tiek izvilkti no tās pašas pamatā esošās populācijas. Šai analīzei temperatūra tiek ignorēta.

• Vai arī augu garumi dažādos temperatūras līmeņos tiek izvilkti no tās pašas pamatā esošās populācijas. Šai analīzei mēslojumu veidi tiek ignorēti.

Aprēķinot atšķirību efektu starp mēslojumu veidiem, kas atrodamas pirmajā punktā ar aizzīmi, un atšķirības pēc temperatūras, kas atrodamas otrajā punktā ar aizzīmēm, seši paraugi, kas pārstāv visus vērtību {mēslojums, temperatūra} pārus, tiek izvilkti no tās pašas populācijas. Alternatīvā hipotēze ir tāda, ka efekti rodas atbilstīgi konkrētiem pāriem {mēslojums, temperatūra} pāri un virs atšķirībām, kas pamatotas tikai uz mēslojumu vai tikai uz temperatūru.

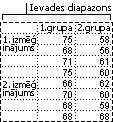
Anova: divfaktors bez replicēšanas

Šis analīzes rīks ir noderīgs, ja dati tiek klasificēti divās dažādās dimensijās kā divu faktoru gadījumā ar replicēšanu. Tomēr šim rīkam ir pieņemts, ka katram pārim ir tikai viens novērojums (piemēram, katrs pāris {mēslojums, temperatūra} iepriekšējā piemērā).

Darblapas funkcija CORRELun PEARSON aprēķina korelācijas koeficientu starp diviem mērījuma mainīgajiem, ja katra mainīgā mērījumi tiek novēroti katrai no N tēmām. (Jebkura tēmas trūkstošā novērojuma rezultātā šī tēma analīzē tiek ignorēta.) Korelācijas analīzes rīks ir īpaši noderīgs, ja katrai no N tēmām ir vairāk nekā divi mērījuma mainīgie. Tā nodrošina izvades tabulu, korelācijas matricu, kurā redzama CORREL (vai PEARSON) vērtība, ko lieto katram iespējamam mērījuma mainīgo pārim.

Korelācijas koeficients, piemēram, kovariācija, ir lielums, kādā divi mērījuma mainīgie "variē kopā". Atšķirībā no kovariācijas korelācijas koeficients tiek mērogots, lai tā vērtība būtu neatkarīga no mērvienībām, kurās tiek izteikti divi mērījuma mainīgie. (Piemēram, ja divi mērījuma mainīgie ir svars un augstums, korelācijas koeficienta vērtība netiek mainīta, ja svars tiek pārvērsts no mārciņām uz mārciņas.) Korelācijas koeficienta vērtībai jābūt no -1 līdz +1 ieskaitot.

Korelācijas analīzes rīku var izmantot, lai pārbaudītu katru mērījuma mainīgo pāri un noteiktu, vai abiem mērījuma mainīgajiem ir tendence pārvietoties kopā — tas ir, viena mainīgā lielajām vērtībām ir tendence būt saistītām ar otra lielajām vērtībām (pozitīvā korelācija), vai viena mainīgā mazajām vērtībām ir tendence būt saistītām ar otra lielajām vērtībām (negatīvā korelācija) vai arī abu mainīgo vērtībām ir tendence būt nesaistītām (korelācija pie 0 (nulle)).

Ja ir N dažādi mērījumu mainīgie, kas novēroti personu kopā, korelācijas un kovariācijas rīkus var izmantot vienā iestatījumā. Korelācijas un kovariācijas rīki dod izvades tabulu, matricu, kas rāda korelācijas koeficientu vai kovariāciju atbilstīgi starp katru mērījuma mainīgo pāri. Atšķirība ir tāda, ka korelācijas koeficienti ir mērogoti atrasties starp -1 un +1 ieskaitot. Atbilstīgās kovariācijas netiek mērogotas. Gan korelācijas koeficients, gan kovariācija ir mērījumi, kurā divi mainīgie "variējas kopā".

Kovariācijas rīks aprēķina darblapas funkcijas COVARIANCE vērtību. P katram mērījuma mainīgo pārim. (KoVARIANCE tieša izmantošana. P, nevis kovariācijas rīks ir saprātīga alternatīva, ja ir tikai divi mērījuma mainīgie, t.i., N=2.) Ieraksts pa kovariācijas rīka izvades tabulas diagonālo daļu i rindā (kolonna i) ir i-tā mērījuma mainīgā kovariance. Tā ir tikai šī mainīgā populācijas dispersija, kā aprēķināta ar darblapas funkciju VAR.P.

Varat izmantot kovariācijas rīku, lai pārbaudītu katru lieluma mainīgo pāri un noteiktu, vai divi lieluma mainīgie tiecas sastapties — tas ir, vai viena mainīgā lielās vērtības var tikt saistītas ar otra mainīgā lielajām vērtībām (pozitīvā kovariācija), vai viena mainīgā mazās vērtības var tikt saistītas ar otra mainīgā lielajām vērtībām (negatīvā kovariācija), vai, iespējams, abu mainīgo vērtības nevar tikt saistītas (kovariācija tuva 0 (nullei)).

Aprakstošās statistikas analīzes rīks ģenerē nemainītās statistikas atskaiti datiem ievades diapazonā, sniedzot informāciju par centrālo tendenci un datu mainīgumu.

Eksponenciālās nogludināšanas analīzes rīks prognozē vērtību, pamatojoties uz iepriekšējā perioda analīzi, kurš ir pielāgots kļūdai šajā iepriekšējā prognozē. Rīks izmanto nogludināšanas konstanti a, kuras lielums nosaka, cik lielā mērā prognozes atbilst kļūdām iepriekšējā prognozē.

F testa divparauga dispersiju analīzes rīks veic divparaugu F testu, lai salīdzinātu divas populācijas dispersijas.

Piemēram, var izmantot F testa rīku laiku paraugos peldēšanas sacensībām katrai no divām komandām. Rīks sniedz nulles hipotēzes testa rezultātu, ka šie divi paraugi nāk no vienādu dispersiju sadalījuma attiecībā pret alternatīvu, ka dispersijas nav vienādas ar spēkā esošajiem sadalījumiem.

Rīks aprēķina F statistikas (vai F proporcijas) vērtību f. Vērtība f tuvu 1 sniedz pierādījumus, ka pamatā esošās populācijas dispersijas ir vienādas. Izvades tabulā, ja f < 1 "P(F <= f) viensekritība" sniedz iespējamību, ka F statistikas vērtība ir mazāka par f, ja populācijas dispersijas ir vienādas, un "F kritiskais viens zars" norāda kritisko vērtību, kas mazāka par 1 izvēlētajam būtiskuma līmenim Alfa. Ja f > 1, "P(F <= f) viens zars" sniedz iespējamību nodrošināt, ka F statistikas vērtība ir lielāka par f, ja populācijas dispersijas ir vienādas, un "F kritiskais viens zars" sniedz kritisko vērtību, kas alfa gadījumā ir lielāka par 1.

Fourier analīzes rīks risina problēmas lineārās sistēmās un analizē periodiskos datus, datu transformēšanai izmantojot ātrās Fourier transformēšanas (FFT) metodi. Šis rīks atbalsta arī inversās transformācijas, kurās transformēto datu inverss tiek atgriezts uz sākotnējiem datiem.

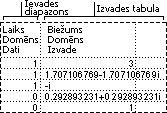
Histogrammas analīzes rīks aprēķina atsevišķos un kumulatīvos sastopamības biežumus šūnas datu diapazonam un datu nodalījumiem. Šis rīks ģenerē datus vērtības gadījumu skaitam datu kopā.

Piemēram, klasē, kurā ir 20 audzēkņi, var noteikt rezultātu izplatību burtu kategorijās. Histogrammas tabula attēlo burtu kategorijas robežas un rezultātu skaitu starp zemāko robežu un pašreizējo robežu. Atsevišķs visbiežākais rezultāts ir datu režīms.

Mainīgā vidējā analīzes rīks projektē vērtības prognozes periodā, pamatojoties uz mainīgā vidējo vērtību konkrētā iepriekšējo periodu skaitā. Vidējais mainīgais sniedz tendences informāciju, ko maskētu visu vēsturisko datu vienkāršs vidējais. Lietojiet šo rīku, lai prognozētu pārdošanu, krājumus vai citas tendences. Katras budžeta vērtības pamatā it tālāk norādītā formula.

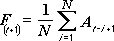
kur:

• N ir iepriekšējo periodu skaits, kas jāiekļauj vidējā mainīgajā

• A j ir faktiskā vērtība laikā j

• F j ir prognozētā vērtība laikā j

Dažādu skaitļu ģenerēšanas analīzes rīks aizpilda diapazonu ar neatkarīgiem dažādiem skaitļiem, kas ir izvilkti no vienas no vairākām izplatībām. Tēmas populācijā var raksturot ar varbūtības sadalījumu. Piemēram, var izmantot parastu izplatību, lai raksturotu personu garumu populāciju, vai arī var izmantot divu iespējamo iznākumu Bernulli sadalījumu, lai raksturotu apgriezto rezultātu populāciju.

Rangu un procentiles analīzes rīks izveido tabulu, kurā ir katras vērtības kārtas un procentuālā rangs datu kopā. Var analizēt vērtību relatīvo novietošanu datu kopā. Šis rīks izmanto darblapas funkcijas RANK. EQ unPERCENTRANK. INC. Ja vēlaties šķirot saistītas vērtības, izmantojiet rank. Funkcija EQ , kas saistītas vērtības apstrādā kā ar vienādu rangu vai izmanto funkciju RANK.Funkcija AVG , kas atgriež saistīto vērtību vidējo rangu.

Regresijas analīzes rīks veic lineārās regresijas analīzi, lietojot "mazāko kvadrātu" metodi, lai caur novērojumu kopu iekļautos līnijā. Var analizēt, kā vienu atkarīgo mainīgo ietekmē vienu vai vairāku neatkarīgo mainīgo vērtības. Piemēram, var analizēt, kā sportista veiktspēju ietekmē tādi faktori kā vecums, garums un svars. Var piešķirt koplietojumus veiktspējas mērvienībā katram no šiem trim faktoriem, pamatojoties uz veiktspējas datu kopu, un pēc tam izmantot rezultātus, lai paredzētu jauna, nepārbaudīta sportista veiktspēju.

Regresijas rīks izmanto darblapas funkciju LINEST.

Iztveršanas analīzes rīks izveido paraugu no populācijas, apstrādājot ievades diapazonu kā populāciju. Ja populācija ir pārāk liela apstrādei vai diagrammai, varat izmantot attēlojošu paraugu. Var izveidot arī paraugu, kurā ir tikai vērtības no konkrētas cikla daļas, ja uzskatāt, ka ievades dati ir periodiski. Piemēram, ja ievades diapazons satur ceturkšņa pārdošanas skaitļus, iztveršana notiek ar periodisku četru vietu pārraides ātrumu vērtībām no tā paša ceturkšņa izvades diapazonā.

Divu paraugu T testa analīzes rīku pārbaude populācijas vienādībai nozīmē, kas ir zem katra parauga. Trīs rīki izmanto dažādus pieņēmumus: ka populācijas dispersijas ir vienādas, ka populācijas dispersijas nav vienādas un ka divi paraugi attēlo pirmsapstrādes un pēcapstrādes novērojumus tām pašām tēmām.

Visiem trim tālāk pieejamajiem rīkiem t statistikas vērtība t tiek aprēķināta un izvades tabulās parādīta kā "t Stat". Atkarībā no datiem šī vērtība, t var būt negatīva vai nenegatīva. Pieņemot, ka pamatā ir vienādi populācijas līdzekļi, ja t < 0, "P(T <= t) viens zars" sniedz iespējamību, ka t-statistikas vērtību var novērot ar negatīvo vērtību nekā t. Ja t >=0, "P(T <= t) viens zars" sniedz varbūtību, ka t-statistikas vērtību var novērot labāk nekā t. "t Kritiskais viens zars" sniedz cutoff vērtību, lai vērotu t-statistikas vērtību, kas ir lielāka vai vienāda ar "t Kritiskais viens zars", ir Alfa.

"P(T <= t) divsekojums" sniedz iespējamību, ka t-statistikas vērtību var novērot lielāku vai vienādu ar t. "P kritiskais divsekojums" sniedz starpības vērtību, tādējādi novērotās t-statistikas iespējamība absolūtajā vērtībā, kas lielāka par "P kritisko divsekojumu", ir alfa.

T tests: divi pāra paraugi vidējiem

Var izmantot pāra testu, ja paraugos ir dabiski novērojumu pāri, piemēram, divreiz testējot paraugu grupu — pirms un pēc eksperimenta. Šis analīzes rīks un tā formula veic divparaugu pāru studenta T testu, lai noteiktu, vai novērojumi, kas tika veikti pirms apstrādes, un novērojumi, kas tika veikti pēc apstrādes, ir nākuši no izplatībām ar vienādiem populācijas vidējiem. Šī T testa forma nepieņem, ka abu populāciju dispersijas ir vienādas.

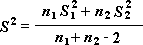
T tests: divu izlašu pieņemšana vienādās dispersijās

Šis analīzes rīks veic divu izlašu studenta T testu. Šī T testa forma pieņem, ka divas datu kopas nāk no sadalījumiem ar vienādām dispersijām. Uz to atsaucas kā uz homoskedastisku T testu. Šo T testu var izmantot, lai noteiktu, cik liela ir iespējamība, ka abi piemēri ir nākuši no sadalījumiem ar vienādiem populācijas vidējiem.

T tests: divu izlašu pieņemšana nevienādās dispersijās

Šis analīzes rīks veic divu izlašu studenta T testu. Šī T testa forma pieņem, ka divas datu kopas nāk no sadalījumiem ar nevienādām dispersijām. Uz to atsaucas kā uz heteroscedastisko T testu. Tāpat kā iepriekšējā vienādo dispersiju gadījumā šo T testu var izmantot, lai noteiktu, vai abi piemēri, kā liekas, ir nākuši no sadalījumiem ar vienādiem populācijas vidējiem. Izmantojiet šo testu, ja abos paraugos ir atšķirīgas tēmas. Izmantojiet pāru testu, kas aprakstīts šajā piemērā, ja ir atsevišķa tēmu kopa un divi paraugi attēlo mērījumus katrai tēmai pirms un pēc apstrādes.

Lai noteiktu statistisko vērtību t, izmanto tālāk norādīto formulu.

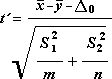
Tālāk norādīto formulu izmanto, lai aprēķinātu brīvības pakāpes df. Tā kā aprēķina rezultāts parasti nav vesels skaitlis, df vērtība tiek noapaļota līdz tuvākajam veselajam skaitlim, lai iegūtu kritisko vērtību no t tabulas. Excel darblapas funkcija T.TEST izmanto aprēķināto df vērtību bez noapaļošanas, jo ir iespējams aprēķināt T vērtību.TEST WITH a nonint iepazīšanās ar df. Tā kā šādas atšķirīgās pieejas ļauj noteikt brīvības pakāpes, T rezultāti.TEST un šis T testa rīks atšķiras nevienlīdzīgo dispersiju gadījumā.

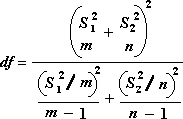
Z tests. Divi means analīzes rīka paraugi veic divus paraugus z testam aprēķināšanai ar zināmām dispersiēm. Šis rīks tiek izmantots, lai pārbaudītu nulles hipotēzes, ka nav atšķirības starp diviem populācijas vērtībām attiecībā pret divpusējām vai divpusējām alternatīvām hipotēzēm. Ja dispersijas nav zināmas, darblapas funkcija Z.Tā vietā ir jāizmanto TEST.

Izmantojot Z testa rīku, uzmanieties, lai pareizi izprastu izvadi. "P(Z <= z) viensekojums" faktiski ir P(Z >= ABS(z)), z vērtības iespējamība tālāk no 0 tajā pašā virzienā kā novērotā z vērtība, ja nav atšķirības starp populācijas līdzekļiem. "P(Z <= z) divsekojums" faktiski ir P(Z >= ABS(z) vai Z <= -ABS(z)), z vērtības iespējamība tālāk no 0 jebkurā virzienā nekā novērotā z vērtība, ja nav atšķirības starp populācijas līdzekļiem. Divsekojumu rezultāts ir vienkārši viensekojuma rezultāts, kas reizināts ar 2. Z testa rīku var arī izmantot gadījumam, kur nulles hipotēze ir tā, ka nav konkrētas vērtības, kas nav nulle atšķirībai starp diviem populācijas vidējiem. Piemēram, šo testu var izmantot, lai noteiktu atšķirības starp divu automašīnu modeļu veiktspēju.