Sprendimo paieškos naudojimas didžiosiomis raidėmis

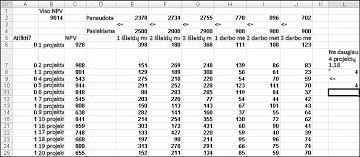
Dauguma korporacijų nori imtis projektų, kurie prisideda prie didžiausios grynosios dabartinės vertės (NPV), atsižvelgiant į ribotus išteklius (paprastai kapitalo ir darbo). Tarkime, kad programinės įrangos kūrimo įmonė bando nustatyti, kurių iš 20 programinės įrangos projektų ji turėtų imtis. NPV (milijonais dolerių) prisidėjo kiekvienas projektas, taip pat kapitalas (milijonais dolerių) ir programuotojų skaičius, reikalingas per ateinančius trejus metus, nurodytas failo Capbudget.xlsx darbalapyje Pagrindinis modelis , kuris pavaizduotas 30–1 pav. kitame puslapyje. Pavyzdžiui, 2 projektas duoda 908 mln. Per 1 metus jai reikia 151 milijono JAV dolerių, 269 mln. 2 projektas reikalauja, kad 139 programuotojai per 1 metus, 86 programuotojai 2 metus ir 83 programuotojai per 3 metus. Langeliuose E4:G4 rodomas kiekvieno iš trejų metų kapitalas (milijonais dolerių), o langeliai H4:J4 nurodo, kiek programuotojų yra prieinama. Pavyzdžiui, per 1 metus galima įsigyti iki 2,5 milijardo dolerių kapitalo ir 900 programuotojų.

Bendrovė turi nuspręsti, ar ji turėtų imtis kiekvieno projekto. Tarkime, kad negalime imtis programinės įrangos projekto dalies; jei mes skirti 0,5 reikalingus išteklius, pavyzdžiui, mes turime ne darbo programą, kad būtų mums $ 0 pajamų!

Modeliavimo situacijose, kuriose jūs arba daryti, arba ko nedaryti gudrybė yra naudoti dvejetainius keičiamus langelius. Dvejetainis kintantis langelis visada lygus 0 arba 1. Kai dvejetainis kintantis langelis, atitinkantis projektą, lygus 1, atliekame projektą. Jei dvejetainis kintantis langelis, atitinkantis projektą, lygus 0, projekto nedarysime. Galite nustatyti, kad sprendimo paieška naudotų dvejetainių keičiamų langelių diapazoną įtraukdami apribojimą, pažymėkite norimus naudoti kintančius langelius, tada dialogo lange Apribojimo įtraukimas esančiame sąraše pasirinkite Bin.

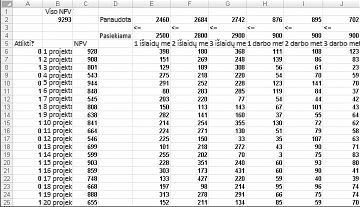
Esant tokiai informacijai esame pasirengę išspręsti programinės įrangos projekto pasirinkimo problemą. Kaip visada naudodami sprendimo paieškos modelį, pirmiausia identifikuojame paskirties langelį, kintančius langelius ir apribojimus.

• Paskirties langelis. Maksimizuojame pasirinktų projektų sugeneruotą NPV.

• Keičiami langeliai. Ieškome 0 arba 1 dvejetainio keitimo langelio kiekvienam projektui. Šiuos langelius radau diapazone A6:A25 (pavadinau diapazono doit). Pavyzdžiui, langelyje A6 esantis 1 nurodo, kad vykdome "Project 1"; 0 langelyje C6 nurodo, kad nesiimame 1 projekto.

• Apribojimus. Turime užtikrinti, kad kiekvienais metais t (t = 1, 2, 3), naudojamas t metų kapitalas yra mažesnis arba lygus t metų kapitalo turimam, o t metų darbas yra mažesnis arba lygus T metų darbui.

Kaip matote, mūsų darbalapis turi apskaičiuoti visus NPV projektus, kasmet naudojamą kapitalą ir kiekvienais metais naudojamus programuotojus. Langelyje B2 naudoju formulę SUMPRODUCT(doit,NPV), kad apskaičiuočiau bendrą pasirinktų projektų sugeneruotą NPV. (Diapazono pavadinimas NPV nurodo diapazoną C6:C25.) Kiekvienam projektui, kurio A stulpelyje yra 1, ši formulė paima projekto NPV, o kiekvienam projektui, kurio A stulpelyje yra 0, ši formulė nepaima projekto NPV. Todėl galime apskaičiuoti visų projektų NPV, o mūsų tikslinis langelis yra tiesinis, nes jis apskaičiuojamas sumavimo terminais, kurie eina po formos (kintantis langelis)*(konstanta). Panašiu būdu apskaičiuoju kiekvienais metais naudojamą kapitalą ir kiekvienais metais naudojamą darbą kopijuoju iš E2 į F2:J2 formulę SUMPRODUCT(doit,E6:E25).

Dabar užpildau dialogo langą Sprendimo paieškos parametrai, kaip parodyta 30-2 pav.

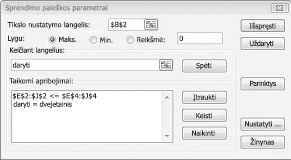
Mūsų tikslas yra maksimizuoti pasirinktų projektų NPV (langelis B2). Mūsų keičiami langeliai (diapazonas, pavadintas doit) yra dvejetainiai keičiami kiekvieno projekto langeliai. Apribojimas E2:J2<=E4:J4 užtikrina, kad kiekvienais metais naudojama kapitalo ir darbo jėga būtų mažesnė arba lygi galimai kapitalo ir darbo jėgai. Norėdami įtraukti apribojimą, dėl kurio keičiami langeliai dvejetainiai, dialogo lange Sprendimo paieškos parametrai spustelėkite Įtraukti ir dialogo lango viduryje esančiame sąraše pasirinkite Bin. Dialogo langas Įtraukti apribojimą turėtų būti rodomas taip, kaip parodyta 30–3 paveikslėlyje.

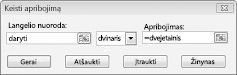
Mūsų modelis yra tiesinis, nes tikslinis langelis yra skaičiuojamas kaip terminų, kurie turi formą (keičia langelį)*(konstanta), suma, o išteklių naudojimo apribojimai apskaičiuojami lyginant sumą (keičiami langeliai)*(konstantos) su konstanta.

Kai dialogo langas Sprendimo paieškos parametrai bus užpildytas, spustelėkite Spręsti ir mes turime anksčiau 30-1 pav. rodomus rezultatus. Rinkdamasi 2, 3, 6–10, 14–16, 19 ir 20 projektus, bendrovė gali gauti ne didesnę kaip 9 293 mln.

Kartais projektų pasirinkimo modeliai turi kitų apribojimų. Pavyzdžiui, jei pasirinksite 3 projektą, taip pat turime pasirinkti "Project 4". Kadangi mūsų dabartinis optimalus sprendimas pasirenka "Project 3", bet ne "Project 4", žinome, kad mūsų dabartinis sprendimas negali likti optimalus. Norėdami išspręsti šią problemą, tiesiog įtraukite apribojimą, kad dvejetainis kintantis langelis, skirtas "Project 3", yra mažesnis arba lygus dvejetainiam keitimo langeliui, skirtam "Project 4".

Šį pavyzdį galite rasti failo Capbudget.xlsx darbalapyje Jei 3 tada 4 , kuris parodytas 30–4 pav. Langelis L9 nurodo dvejetainę reikšmę, susijusią su "Project 3", o langelį L12 – su dvejetaine reikšme, susijusia su "Project 4". Įtraukdami L9 apribojimą<=L12, jei pasirenkame "Project 3", L9 lygu 1, o mūsų apribojimas L12 ("Project 4" dvejetainis) lygus 1. Mūsų apribojimas taip pat turi palikti dvejetainę reikšmę "Project 4" keičiamame langelyje neapribotą, jei nepažymėsime "Project 3". Jei nepasirinksime 3 projekto, L9 lygu 0, o mūsų apribojimas leidžia "Project 4" dvejetainį lygų 0 arba 1, ko norime. Naujas optimalus tirpalas parodytas 30-4 paveiksle.

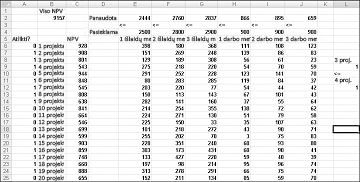
Naujas optimalus sprendimas apskaičiuojamas, jei pasirinkus "Project 3" taip pat reikia pasirinkti "Project 4". Dabar tarkime, kad galime atlikti tik keturis projektus iš 1–10 projektų. (Žr. darbalapį Daugiausia 4 iš P1–P10 , kaip parodyta 30–5 paveiksle.) Langelyje L8 mes apskaičiuojame dvejetainių reikšmių, susietų su projektais nuo 1 iki 10, sumą su formule SUM(A6:A15). Tada įtraukiame L8 apribojimą<=L10, kuris užtikrina, kad būtų pasirinkta ne daugiau kaip 4 pirmieji 10 projektų. Naujas optimalus tirpalas parodytas 30–5 paveiksle. NPV nukrito iki 9,014 mlrd.

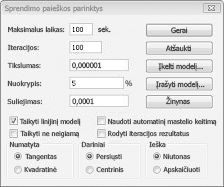
Linijinės sprendimo paieškos modeliai, kuriuose kai kurie arba visi keičiami langeliai turi būti dvejetainiai arba sveikieji, paprastai yra sudėtingesni nei linijiniai modeliai, kuriuose visi keičiami langeliai gali būti trupmenos. Dėl šios priežasties dažnai esame patenkinti beveik optimaliu dvejetainio arba sveikojo skaičiaus programavimo problemos sprendimu. Jei sprendimo paieškos modelis veikia ilgą laiką, galbūt norėsite pakoreguoti parametrą Leistinas nuokrypis dialogo lange Sprendimo paieškos parinktys. (Žr. 30–6 pav.) Pvz., 0,5 % nuokrypio parametras reiškia, kad sprendimo paieška nustos veikti pirmą kartą radus įvykdomą sprendimą, kuris neviršija 0,5 procento teorinės optimalios tikslinio langelio reikšmės (teorinė optimali tikslinio langelio reikšmė yra optimali tikslinė reikšmė, rasta, kai nenurodyti dvejetainiai ir sveikojo skaičiaus apribojimai). Dažnai mes susiduriame su pasirinkimu tarp rasti atsakymą per 10 procentų optimalaus per 10 minučių arba rasti optimalų sprendimą per dvi savaites kompiuterio laiko! Numatytoji leistino nuokrypio reikšmė yra 0,05 %, o tai reiškia, kad sprendimo paieška sustoja, kai randa tikslinę langelio reikšmę 0,05 proc. teorinės optimalios tikslinės langelio reikšmės.

1. Įmonėje svarstomi devyni projektai. NPV, pridėta prie kiekvieno projekto, ir kapitalas, reikalingas kiekvienam projektui per ateinančius dvejus metus, parodytas toliau pateiktoje lentelėje. (Visi skaičiai yra milijonais.) Pvz., 1 projektas pridės 14 milijonų JAV dolerių NPV ir reikės 12 milijonų JAV dolerių išlaidų per 1 metus ir 3 mln. Per 1 metus projektams galima įsigyti 50 mln.

	NPV	1 metų išlaidos	2 metų išlaidos
1 projektas	14	12	3
2 projektas	17	54	7
3 projektas	17	6	6
4 projektas	15	6	2
5 projektas	40	30	35
"Project 6"	12	6	6
7 projektas	14	48	4
8 projektas	10	36	3
9 projektas	12	18	3

• Jei negalime imtis dalies projekto, bet turime imtis visų arba nė vieno projekto, kaip galėtume maksimaliai padidinti NPV?

• Tarkime, kad jei įgyvendinamas 4 projektas, turi būti įgyvendinamas 5 projektas. Kaip mes galime maksimaliai padidinti NPV?

• Publikavimo įmonė bando nustatyti, kurias iš 36 knygų ji turėtų publikuoti šiais metais. Failo Pressdata.xlsx pateikia šią informaciją apie kiekvieną knygą:

  • Numatomos pajamos ir plėtros išlaidos (tūkstančiais dolerių)

  • Kiekvienos knygos puslapiai

  • Ar knyga skirta programinės įrangos kūrėjų auditorijai (nurodyta E stulpelyje nurodytu 1)

    Publikavimo įmonė gali publikuoti knygas, kurių suma šiais metais sudaro iki 8500 puslapių, ir publikuoti bent keturias knygas, kurios pritaikytos programinės įrangos kūrėjams. Kaip įmonė gali padidinti savo pelną?

Šis straipsnis buvo pritaikytas iš "Microsoft Office Excel 2007" duomenų analizės ir verslo modeliavimo pagal Wayne L. Winston.

Ši klasės stiliaus knyga buvo sukurta iš pristatymų serijos Wayne Winston, gerai žinomas statistikos ir verslo profesorius, kuris specializuojasi kūrybinių, praktinių programų Excel.