Calculates the net present value of an investment by using a discount rate and a series of future payments (negative values) and income (positive values).
Syntax
NPV(rate,value1,value2,...)
Rate is the rate of discount over the length of one period.
Value1, value2,... are 1 to 29 arguments representing the payments and income. Value1, value2,... must be equally spaced in time and occur at the end of each period. NPV uses the order of value1, value2,... to interpret the order of cash flows. Be sure to enter your payment and income values in the correct sequence. Arguments that are numbers, empty, logical values, or text representations of numbers are counted; arguments that are error values or text that cannot be translated into numbers are ignored.
Remarks
-
The NPV investment begins one period before the date of the value1 cash flow and ends with the last cash flow in the list. The NPV calculation is based on future cash flows. If your first cash flow occurs at the beginning of the first period, the first value must be added to the NPV result, not included in the values arguments. For more information, see the examples below.
-
If n is the number of cash flows in the list of values, the formula for NPV is:
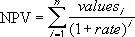
-
NPV is similar to the PV function (present value). The primary difference between PV and NPV is that PV allows cash flows to begin either at the end or at the beginning of the period. Unlike the variable NPV cash flow values, PV cash flows must be constant throughout the investment. For information about annuities and financial functions, see PV.
Example 1
In the following example:
-
Rate is the annual discount rate.
-
Value1 is the initial cost of investment one year from today.
-
Value2 is the return from first year.
-
Value3 is the return from second year.
-
Value4 is the return from third year.
In the example, you include the initial $10,000 cost as one of the values, because the payment occurs at the end of the first period.
|
Rate |
Value1 |
Value2 |
Value3 |
Value4 |
Formula |
Description (Result) |
|---|---|---|---|---|---|---|
|
10% |
-10000 |
3000 |
4200 |
6800 |
=NPV([Rate], [Value1], [Value2], [Value3], [Value4]) |
Net present value of this investment (1,188.44) |
Example 2
In the following example:
-
Rate is the annual discount rate. This might represent the rate of inflation or the interest rate of a competing investment.
-
Value1 is the initial cost of investment one year from today.
-
Value2 is the return from first year.
-
Value3 is the return from second year.
-
Value4 is the return from third year.
-
Value5 is the return from fourth year.
-
Value6 is the return from fifth year.
In the example, you don't include the initial $40,000 cost as one of the values, because the payment occurs at the beginning of the first period.
|
Rate |
Value1 |
Value2 |
Value3 |
Value4 |
Value5 |
Value6 |
Formula |
Description (Result) |
|---|---|---|---|---|---|---|---|---|
|
8% |
-40000 |
8000 |
9200 |
10000 |
12000 |
14500 |
=NPV(Rate, [Value2], [Value3], [Value4], [Value5], [Value6])+[Value1] |
Net present value of this investment (1,922.06) |
|
8% |
-40000 |
8000 |
9200 |
10000 |
12000 |
14500 |
=NPV(Rate, [Value2], [Value3], [Value4], [Value5], [Value6], -9000)+[Value1] |
Net present value of this investment, with a loss in the sixth year of 9000 (-3,749.47) |










