企業がソルバーを使用して、実行する必要があるプロジェクトを決定するにはどうすればよいですか?
毎年、Eli Lilly のような会社は、開発する医薬品を決定する必要があります。Microsoft のような会社。開発するソフトウェア プログラム。Proctor & Gamble のような新しいコンシューマー製品を開発する会社。 Excel のソルバー機能は、会社がこれらの決定を行うのに役立ちます。
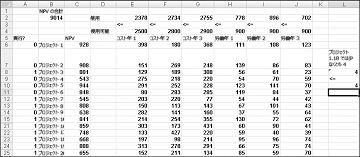
ほとんどの企業は、限られたリソース (通常は資本と労働) に従って、最大の正味現在価値 (NPV) に貢献するプロジェクトを行いたいと考えています。 たとえば、あるソフトウェア開発会社が、20 のソフトウェア プロジェクトのうちどれを実行すべきかを判断しようとしているとします。 各プロジェクトによって貢献された NPV (数百万ドル単位) と、次の 3 年間に必要な資本 (数百万ドル単位) とプログラマの数は、ファイル Capbudget.xlsx の Basic Model ワークシートに示されています。これは、次のページの図 30-1 に示されています。 たとえば、Project 2 の利回りは 9 億8000 万ドルです。 1 年目は 1 億 5,100 万ドル、2 年目は 2 億 6,900 万ドル、3 年目には 2 億 4,800 万ドルが必要です。 Project 2 には、1 年に 139 人のプログラマー、2 年目に 86 人のプログラマー、3 年目に 83 人のプログラマーが必要です。 セル E4:G4 は、各 3 年間に使用可能な資本 (数百万ドル) を示し、セル H4:J4 は使用可能なプログラマの数を示します。 たとえば、1 年目には最大 25 億ドルの資本と 900 人のプログラマが利用できます。
会社は、各プロジェクトを引き受ける必要があるかどうかを決定する必要があります。 ソフトウェア プロジェクトの一部を引き受けることができないとします。たとえば、必要なリソースの 0.5 を割り当てると、$0 の収益をもたらす非稼働プログラムが作成されます。
あなたが何かをする、または何もしない状況のモデリングのトリックは、 バイナリ変更セルを使用することです。 バイナリ変更セルは常に 0 または 1 に等しくなります。 プロジェクトに対応するバイナリ変更セルが 1 と等しい場合は、プロジェクトを実行します。 プロジェクトに対応するバイナリ変更セルが 0 の場合、プロジェクトは実行されません。 制約を追加してバイナリ変更セルの範囲を使用するようにソルバーを設定します。使用する変更セルを選択し、[制約の追加] ダイアログ ボックスの一覧から [ビン] を選択します。
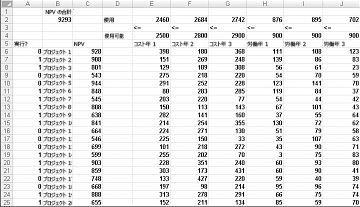
この背景から、ソフトウェア プロジェクトの選択の問題を解決する準備ができました。 ソルバー モデルと同様に、まずターゲット セル、変更セル、制約を特定します。
-
ターゲット セル。 選択したプロジェクトによって生成される NPV を最大化します。
-
セルの変更。 プロジェクトごとに 0 または 1 のバイナリ変更セルを探します。 私はこれらのセルを範囲A6:A25(そして範囲 ditという名前)に配置しました。 たとえば、セル A6 の 1 は、Project 1 を引き受けることを示します。セル C6 の 0 は、Project 1 を引き受けなかったことを示します。
-
制約。 各年 t (t=1、2、3)、使用される t 年の資本が使用可能な年 t 資本以下であることを確認する必要があります。また、使用される 1 年分の労働が利用可能な年 t 労働以下であることを確認する必要があります。
ご覧のとおり、ワークシートでは、NPV、毎年使用される資本、および毎年使用されるプログラマのプロジェクトの選択を計算する必要があります。 セル B2 では、 SUMPRODUCT(doit,NPV) という数式を使用して、選択したプロジェクトによって生成された NPV の合計を計算します。 (範囲名 NPV は範囲 C6:C25 を参照します)。 列 A に 1 を持つすべてのプロジェクトについて、この数式はプロジェクトの NPV を取得し、列 A に 0 を持つすべてのプロジェクトについて、この数式はプロジェクトの NPV を取得しません。 したがって、すべてのプロジェクトの NPV を計算できます。ターゲット セルは、フォームに従う用語 (セルの変更) *(定数) を合計することによって計算されるため、線形です。 同様に、私は毎年使用される資本と、E2からF2:J2に式 SUMPRODUCT(doit,E6:E25)をコピーして、毎年使用される労働を計算します。
図 30-2 に示すように、[ソルバー パラメーター] ダイアログ ボックスに入力します。
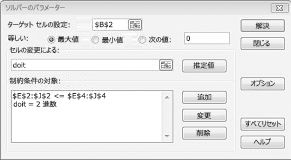
目標は、選択したプロジェクト (セル B2) の NPV を最大化することです。 変更セル ( doit という名前の範囲) は、各プロジェクトのバイナリ変更セルです。 制約 E2:J2<=E4:J4 は、毎年、使用される資本と労働が利用可能な資本と労働以下であることを保証します。 セルの変更をバイナリにする制約を追加するには、[ソルバー パラメーター] ダイアログ ボックスで [追加] をクリックし、ダイアログ ボックスの中央にある一覧から [ビン] を選択します。 図 30-3 に示すように、[制約の追加] ダイアログ ボックスが表示されます。
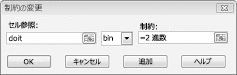
ターゲット セルはフォーム (変更セル)*(定数) を持つ項の合計として計算され、リソース使用量の制約は (セルの変化 ) *( 定数) の合計を定数と比較することによって計算されるため、モデルは線形です。
[ソルバー パラメーター] ダイアログ ボックスが入力された状態で、[解析] をクリックすると、図 30-1 で前に示した結果が表示されます。 同社は、プロジェクト 2、3、6-10、14-16、19、および 20 を選択することで、最大 NPV 9,293 百万ドル (92 億 9,300 万ドル) を取得できます。
プロジェクト選択モデルに他の制約がある場合があります。 たとえば、Project 3 を選択した場合、Project 4 も選択する必要があるとします。 現在の最適なソリューションは Project 3 を選択しますが、Project 4 は選択していないため、現在のソリューションは最適なままではいられないことがわかります。 この問題を解決するには、Project 3 のバイナリ変更セルが Project 4 のバイナリ変更セル以下であるという制約を追加するだけです。
この例は、図 30-4 に示されているファイル Capbudget.xlsx の If 3 と 4 ワークシートにあります。 セル L9 は Project 3 に関連するバイナリ値を参照し、セル L12 は Project 4 に関連するバイナリ値を示します。 制約 L9<=L12 を追加することで、Project 3 を選択した場合、L9 は 1 に等しく、制約によって L12 (Project 4 バイナリ) が 1 になります。 また、Project 3 を選択しない場合、制約は Project 4 の変更セルにバイナリ値を無制限のままにする必要があります。 Project 3 を選択しない場合、L9 は 0 に等しく、Project 4 バイナリは 0 または 1 に等しくなります。 新しい最適解を図30-4に示します。
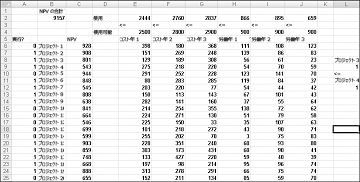
プロジェクト 3 を選択すると、Project 4 も選択する必要がある場合は、新しい最適なソリューションが計算されます。 次に、プロジェクト 1 から 10 の間で実行できるプロジェクトは 4 つだけであるとします。 (図 30-5 に示されている P1 から P10 のワークシートの最大 4 個を参照してください)。 セル L8 では、式 SUM(A6:A15) を使用して、Projects 1 から 10 に関連付けられているバイナリ値の合計を計算します。 次に、制約 L8<=L10 を追加します。これにより、最初の 10 個のプロジェクトのうち最大で 4 個が選択されます。 新しい最適解を図30-5に示す。 NPV は 90 億 1400 万ドルに減少しました。
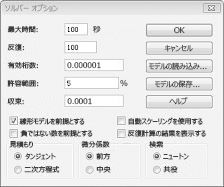
一部またはすべての変更セルがバイナリまたは整数である必要がある線形ソルバー モデルは、通常、すべての変更セルを分数にできる線形モデルよりも解きにくいです。 このため、多くの場合、バイナリまたは整数プログラミングの問題に対する最適なソリューションに満足しています。 ソルバー モデルが長時間実行される場合は、[ソルバー オプション] ダイアログ ボックスの [許容値] 設定を調整することを検討してください。 (図 30-6 を参照)。 たとえば、許容値を 0.5% に設定すると、理論上の最適なターゲット セル値の 0.5% 以内の実行可能な解が初めて検出されたときにソルバーが停止します (理論上の最適なターゲット セル値は、2 項制約と整数制約が省略されたときに見つかった最適なターゲット値です)。 多くの場合、10 分で最適の 10% 以内に回答を見つけるか、コンピューター時間の 2 週間で最適なソリューションを見つけるかの選択に直面しています。 既定の許容値は 0.05% です。これは、理論上の最適なターゲット セル値の 0.05% 以内のターゲット セル値が検出されるとソルバーが停止することを意味します。
-
ある会社では、9 つのプロジェクトが検討されています。 次の表に、各プロジェクトによって追加された NPV と、次の 2 年間に各プロジェクトに必要な資本を示します。 (すべての数値は百万単位です。 たとえば、Project 1 では NPV に 1,400 万ドルが追加され、1 年目には 1,200 万ドル、2 年目には 300 万ドルの支出が必要です。 1 年目には、プロジェクトで 5,000 万ドルの資本を利用でき、2 年目には 2,000 万ドルを利用できます。
|
NPV |
1 年目の支出 |
2 年目の支出 |
|
|---|---|---|---|
|
Project 1 |
14 |
12 |
3 |
|
Project 2 |
17 |
54 |
7 |
|
Project 3 |
17 |
6 |
6 |
|
Project 4 |
15 |
6 |
2 |
|
Project 5 |
40 |
30 |
35 |
|
Project 6 |
12 |
6 |
6 |
|
Project 7 |
14 |
48 |
4 |
|
Project 8 |
10 |
36 |
3 |
|
Project 9 |
12 |
18 |
3 |
-
プロジェクトの一部を引き受けることができないが、プロジェクトのすべてまたはいずれも引き受けなければならない場合、NPV を最大化するにはどうすればよいですか?
-
プロジェクト 4 が実施されている場合、Project 5 を実行する必要があるとします。 NPV を最大化するにはどうすればよいですか?
-
ある出版社は、今年発行する必要がある 36 冊の書籍のうちどれを決定しようとしています。 ファイル Pressdata.xlsx は、各書籍に関する次の情報を提供します。
-
予想される収益と開発コスト (数千ドル)
-
各書籍のページ
-
本がソフトウェア開発者の対象ユーザーを対象にしているかどうか (列 E の 1 で示されます)
ある出版社は、今年最大 8500 ページの書籍を発行でき、ソフトウェア開発者向けに少なくとも 4 冊の書籍を発行する必要があります。 会社はどのようにして利益を最大化できますか?
-
この記事は、 Microsoft Office Excel 2007 Data Analysis and Business Modeling by Wayne L. Winston から適用されています。
このクラスルームスタイルの本は、Excelのクリエイティブで実用的なアプリケーションを専門とする有名な統計学者でビジネス教授のウェイン・ウィンストンによる一連のプレゼンテーションから開発されました。










