複雑な統計学的分析や工学的分析を行わなければならない場合も、分析ツールを使用すれば、すばやく簡単に結果を得ることができます。 分析に必要なデータとパラメーターを指定すると、各ツールが統計用または工学用の適切なマクロ関数を使ってデータを分析し、計算結果を出力テーブルに表示します。 出力テーブルだけでなく、グラフを出力するツールもあります。
データ分析関数は、一度に 1 つのワークシートでのみ使用できます。 グループ化されたワークシートでデータ分析を実行すると、分析結果は 1 枚目のワークシートに表示され、残りのワークシートには空のテーブルが表示されます。 残りのワークシートでデータ分析を実行するには、ワークシートごとに分析ツールで再計算します。
分析ツールには、以降のセクションで説明するツールが含まれます。 これらのツールにアクセスするには、[データ] タブの [分析] グループで [データ分析] をクリックします。 [データ分析] が表示されない場合は、分析ツール アドイン プログラムを読み込む必要があります。
-
[ファイル] タブをクリックします。[オプション] をクリックし、[アドイン] カテゴリをクリックします。
-
[管理] ボックスの一覧の [Excel アドイン] をクリックし、[設定] をクリックします。
Excel for Mac を使用している場合は、ファイル メニューで [ツール]、[Excel アドイン] の順に選択します。
-
[アドイン] ボックスで、[分析ツール] チェック ボックスをオンにし、[OK] をクリックします。
-
[有効なアドイン] ボックスの一覧に [分析ツール] が表示されない場合は、[参照] をクリックしてアドイン ファイルを見つけます。
-
分析ツールが現在コンピューターにインストールされていないというメッセージが表示されたら、[はい] をクリックして分析ツールをインストールします。
-
注: 分析ツールで Visual Basic for Application (VBA) 関数を使用するには、分析ツールを読み込むときと同じ方法で "分析ツール - VBA" アドインを読み込みます。 [使用できるアドイン] ボックスの一覧の [分析ツール - VBA] チェック ボックスをオンにします。
分散分析ツールを使用すると、さまざまな種類の分散分析を行うことができます。 使用するツールは、検定する母集団の要因数と標本数によって決まります。
分散分析: 一元配置
このツールは、複数の標本のデータについて分散の簡単な分析を行います。 この分析を行うと、すべての標本に関して基になる確率分布が同じではないという対立仮説に対して同じ確率分布からそれぞれの標本が得られるという仮説を検定することができます。 標本が 2 つのみの場合は、T.TEST ワークシート関数を使用できます。 3 つ以上の標本については T.TEST 関数は利用できませんが、代わりに一元配置分散分析モデルを使うことができます。
分散分析: 繰り返しのある二元配置
この分析ツールは、データを 2 つの異なる次元に従って分類できる場合に役立ちます。 たとえば植物の高さを計測する実験では、その植物に A、B、C など異なる肥料を与え、低温、高温などの異なる温度環境に置く場合があります。 {肥料、温度} の 6 種類の可能な組み合わせのそれぞれについて、植物の高さを同じ回数観察します。 この分散分析ツールを使うと、以下の検定を行うことができます。
-
異なる種類の肥料を与えた場合の植物の高さが、同じ母集団から得られた標本であると見なせるかどうか。 この分析では温度環境を無視します。
-
異なる温度環境に置いた場合の植物の高さが、同じ母集団から得られた標本であると見なせるかどうか。 この分析では肥料の種類を無視します。
箇条書き項目 1 での肥料の種類と箇条書き項目 2 での温度環境の違いによる影響を考慮に入れて、{肥料、温度} 値のすべての組み合わせを代表する 6 つの標本が同じ母集団から得られたものであると見なせるかどうかを検定します。 この場合の対立仮説は、肥料の種類単独または温度環境単独における違いに対して、{肥料、温度} の特定の組み合わせによる影響があるということです。

分散分析: 繰り返しのない二元配置
この分析ツールは、繰り返しのある二元配置の場合と同じように、データが 2 つの異なる次元で分類される場合に役立ちます。 ただしこのツールでは、1 つの組み合わせ (たとえば前の例では、{肥料、温度} の組み合わせの 1 つ) について、1 回の観察のみを行うと仮定します。
CORREL および PEARSON ワークシート関数は両方とも、N 人の被験者のそれぞれについて各変数の測定値が観察されたときに、2 つの測定変数間の相関係数を計算します。 (対象の観察が欠落していると、その対象は分析で無視されます。) 相関分析ツールは、N 人の被験者のそれぞれに 3 つ以上の測定変数がある場合に特に役立ちます。 これは、測定変数の可能な各ペアに適用される CORREL (または PEARSON) の値を示す出力テーブル、相関行列を提供します。
相関係数は、共分散と同様に、2 つの測定変数が「一緒に変化する」程度の尺度です。 共分散とは異なり、相関係数は、その値が 2 つの測定変数が表される単位に依存しないようにスケーリングされます。 (たとえば、2 つの測定変数が重量と高さの場合、重量をポンドからキログラムに変換しても、相関係数の値は変わりません。) 相関係数の値は、-1 から +1 の間である必要があります。
相関分析ツールを使うと、測定変数の組み合わせそれぞれについて 2 つの測定変数が一緒に変化する傾向があるかどうかを調べることができます。一方の変数の大きな値がもう一方の変数の大きな値と関連する傾向があるか (正の相関)、一方の変数の小さな値がもう一方の変数の大きな値と関連する傾向があるか (負の相関)、両方の変数の値が関連しない傾向があるか (0 に近い相関) などを調べることができます。
一連の個人で N 個の異なる測定変数が観測されている場合、相関ツールと共分散ツールはどちらも同じ設定で使用できます。 相関ツールと共分散ツールはそれぞれ、測定変数の各ペア間の相関係数または共分散をそれぞれ示す出力テーブル、行列を提供します。 違いは、相関係数が -1 と +1 の間にあるようにスケーリングされることです。 対応する共分散はスケーリングされません。 相関係数と共分散はどちらも、2 つの変数が「一緒に変化する」程度の尺度です。
共分散ツールは、測定変数の各ペアのワークシート関数 COVARIANCE.P の値を計算します。 (測定変数が 2 つしかない場合、つまり N=2 の場合は、共分散ツールではなく COVARIANCE.P を直接使用するのが妥当な代替手段です。) 行 i 、列 i の共分散ツールの出力テーブルの対角線上のエントリは、i 番目の測定変数とそれ自体の共分散です。 これは、ワークシート関数 VAR によって計算された、その変数の母分散にすぎません。P。
共分散分析ツールを使うと、測定変数の組み合わせそれぞれについて 2 つの測定変数が一緒に変化する傾向があるかどうかを調べることができます。一方の変数の大きな値がもう一方の変数の大きな値と関連する傾向があるか (正の共分散)、一方の変数の小さな値がもう一方の変数の大きな値と関連する傾向があるか (負の共分散)、両方の変数の値が関連しない傾向があるか (0 に近い共分散) などを調べることができます。
基本統計量分析ツールは、入力範囲のデータを対象に、一変量による基本統計量を調べ、対象となるデータの主要な傾向と変動に関する情報を出力します。
指数平滑化分析ツールは、前の期間の予測に基づいて、その前の予測の誤差を調整した値を予測します。 平滑化定数 a を使って計算します。この定数は、前回の予測値の誤差に対する予測値の反応の強さを決める値です。
注: 平滑化定数に指定する値は 0.2 ~ 0.3 が適しています。 この範囲の値を使うと、現在の予測が前回の予測の 20 ~ 30% の誤差に調整されます。 定数に大きい値を指定すると、予測値の計算に必要な時間は短くなりますが、予測の誤差は大きくなります。 定数に小さい値を指定すると、予測値の計算に必要な時間が長くなります。
F 検定: 2 標本を使った分散の検定分析ツールは、2 つの標本を使った F 検定を行って、2 つの母集団の分散を比較します。
たとえば、2 つのチームそれぞれの水泳大会でのタイムの標本について F 検定ツールを使用することができます。 このツールを使用すると、基となる分布で分散が等しくないという対立仮説に対して、分散が等しい分布からこれら 2 つの標本が得られるという帰無仮説に対する検定の結果を求めることができます。
このツールは F 統計 (または F 比率) の f 値を計算します。 f の値が 1 に近い場合は、基になる母集団の分散が等しいことを示します。 出力テーブルでは、f < 1 の場合、"P(F <= f) 片側" で、母集団の分散が等しいときに f より小さい F 統計の値が測定される確率が求められ、"F 境界値 片側" で、選択した基準値のレベル Alpha に対して 1 未満の境界値が求められます。 f > 1 の場合は、"P(F <= f) 片側" で、母集団の分散が等しいときに f より大きい F 統計の値が測定される確率が求められ、"F 境界値 片側" で、選択したレベル Alpha に対して 1 を超える境界値が求められます。
フーリエ解析分析ツールは、データを変換する高速フーリエ変換 (FFT) を使って線形システムの解を求め、周期データを分析します。 この分析ツールは、変換したデータを元のデータに戻す逆変換もサポートしています。
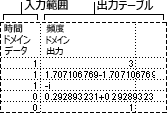
移動平均分析ツールは、過去の一定期間の変数の平均値に基づき、将来の期間の値を予測します。 移動平均を使うと、過去のデータを平均するだけではわからない傾向についての情報が得られます。 売り上げや在庫などの傾向を予測するには、この分析ツールを使用します。 予測値は、次の数式を基に計算されます。
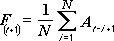
ここで
-
N は、移動平均の計算に使う過去の観測値の個数です。
-
A j は、j 回目の観測値です。
-
F j は、j 回目の予測値です。
乱数生成分析ツールは、いくつかの分布の 1 つから抽出された独立した乱数で範囲を埋めます。 確率分布を使用して、母集団内の対象を特徴付けることができます。 たとえば、正規分布を使用して個人の身長の母集団を特徴付けたり、2 つの可能な結果のベルヌーイ分布を使用してコイン トスの結果の母集団を特徴付けたりすることができます。
順位と百分位数分析ツールは、対象となるデータ グループに含まれる各値に対して、その順位と百分位を含む出力テーブルを作成します。 データの中での各値の相対的な位置を分析できます。 このツールは RANK.EQ ワークシート関数と PERCENTRANK.INC ワークシート関数を使用します。 同じ値を考慮に入れる場合は、RANK.EQ 関数を使用するか (同じ値は同じ順位として扱われる)、RANK.AVG 関数を使用します (同じ値については順位の平均を返す)。
回帰分析ツールは、「最小二乗」法を使用して線形回帰分析を実行し、一連の観測値に線を当てはめます。 単一の従属変数が 1 つ以上の独立変数の値によってどのように影響を受けるかを分析できます。 たとえば、年齢、身長、体重などの要因によってアスリートのパフォーマンスがどのように影響を受けるかを分析できます。 一連のパフォーマンス データに基づいて、パフォーマンス測定値のシェアをこれら 3 つの要素のそれぞれに割り当て、その結果を使用して、テストされていない新しいアスリートのパフォーマンスを予測できます。
回帰分析ツールは LINEST ワークシート関数を使用します。
サンプリング分析ツールは、入力範囲のデータを母集団と見なし、母集団から標本を抽出します。 母集団の規模が大きすぎて統計処理やグラフ化が困難な場合は、母集団全体ではなく標本を対象に分析すると便利です。 また、入力データにある種の周期性が認められる場合は、周期の特定部分から一定数の標本を抽出することもできます。 たとえば、入力範囲に四半期ごとの売上高が入力されている場合、周期を 4 に設定すると、同じ四半期の売上高だけを出力テーブルに抽出できます。
2 標本による t 検定分析ツールは、各標本の基になる母集団の平均の等しさを検定します。 母集団の分散が等しいという仮定、母集団の分散が等しくないという仮定、および 2 つの標本が同じ対象物についての処理の前と後の測定を表すという仮定、という 3 つの異なる仮定に 3 つのツールを使用します。
以下の 3 つのツールすべてにおいて、t 統計値 t が計算されて出力テーブルに "t Stat" として示されます。 データに応じてこの t という値は負の値にも正の値にもなります。 基になる母集団の平均値が等しいとする仮定では、t < 0 の場合、"P(T <= t) 片側" で、t より小さい t 統計の値が測定される確率が求められます。 t >=0 の場合は、"P(T <= t) 片側" で、t より大きい t 統計の値が測定される確率が求められます。 "t 境界値 片側" で、"t 境界値 片側" より大きいか等しい t 統計の値が測定される確率が Alpha になるような区分値が求められます。
"P(T <= t) 両側" で、絶対値が t よりも大きい t 統計の値が測定される確率が求められます。 "P 境界値 両側" で、絶対値が "P 境界値 両側" より大きい t 統計の値が測定される確率が Alpha になるような区分値が求められます。
t 検定: 一対の標本による平均の検定
1 つの標本グループをある実験の前後で 2 度検定する場合のように、2 つの観測値に自然な対の関係がある場合は、この形式の t 検定を使います。 この分析ツールとその数式は、一対の標本を使ったスチューデントの t 検定を行い、処理の前に行われた測定と処理の後に行われた測定が、母集団の平均値が等しい分布から行われたと見なせるかどうかを調べます。 この形式の t 検定では、2 つの母集団の分散が等しいことを前提としません。
注: この分析ツールを使って出力する結果には、次の数式で求められる、プールされた分散 (結果に関するデータの分散がプールされた量) が現れることもあります。
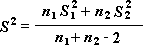
t 検定: 等分散を仮定した 2 標本による検定
この分析ツールは、2 標本のスチューデントの t 検定を実行します。 この t 検定フォームは、2 つのデータ セットが同じ分散の分布からのものであることを前提としています。 これは、等分散性 t 検定と呼ばれます。 この t 検定を使用して、2 つのサンプルが母集団の平均が等しい分布からのものである可能性が高いかどうかを判断できます。
t 検定: 分散が等しくないと仮定した 2 標本による検定
この分析ツールは、2 標本のスチューデントの t 検定を実行します。 この t 検定フォームは、2 つのデータ セットが不均等な分散を持つ分布からのものであることを前提としています。 これは、不均一分散 t 検定と呼ばれます。 前の等分散の場合と同様に、この t 検定を使用して 2 つのサンプルが母集団の平均が等しい分布からのものである可能性が高いかどうかを判断できます。 2 つのサンプルに異なる被験者がいる場合は、このテストを使用します。 次の例で説明するペア検定を使用します。これは、被験者のセットが 1 つで、2 つのサンプルが治療前後の各被験者の測定値を表す場合です。
統計定数 t を決めるには、次の数式を使います。
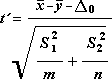
自由度 df を計算するには、次の数式を使用します。 通常は計算結果が整数ではないため、t テーブルからの境界値を求める際に、df の値が最も近い整数に四捨五入されます。 Excel のワークシート関数 T.TEST は、整数以外の df 値で T.TEST の値を計算できるため、計算された df 値が四捨五入されずそのまま使われます。 自由度を決める方法のこの違いのために、異分散における T.TEST とこの t 検定ツールの結果は異なります。
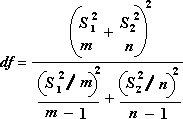
z 検定: 2 標本による平均の検定分析ツールは、既知の分散を使って、2 つの標本を対象に平均値の z 検定を行います。 この分析ツールを使って、片面または両面の対立仮説いずれかに対して 2 つの母集団の平均値の間に差がないという帰無仮設を検定します。 分散が未知の場合は、代わりに Z.TEST ワークシート関数を使う必要があります。
z 検定分析ツールを使う場合は、出力を詳しく調べる必要があります。 "P(Z <= z) 片側" は実際には P(Z >= ABS(z)) を表し、母集団の平均値に差がない場合、z 値の確率は測定される z 値と同じ方向に 0 から遠い値になります。 "P(Z <= z) 両側" は実際には P(Z >= ABS(z) or Z <= -ABS(z)) を表し、母集団の平均値に差がない場合、z 値の確率は測定される z 値のいずれかの方向に 0 から遠い値になります。 両側の結果は、片側のちょうど 2 倍の値になります。 z 検定分析ツールは、2 つの母集団の平均値の差が 0 以外の特定の値であるという仮説が帰無仮説となる場合に使用することもできます。 たとえば、z 検定を行うと、2 種類の車の性能の差異を検定できます。
補足説明
Excel Tech Communityで、いつでも専門家に質問できます。また、コミュニティでは、サポートを受けられます。










