Questo articolo descrive la sintassi della formula e l'uso della funzione TEST.Z in Microsoft Excel.
Restituisce il valore di probabilità a una coda di un test z. Ipotizzando una determinata media della popolazione µ0, TEST.Z restituisce la probabilità che la media campione sia maggiore della media di osservazioni nel set di dati (matrice), ovvero della media campione osservata.
Per informazioni sulla modalità di utilizzo di TEST.Z per il calcolo di un valore di probabilità a due code, vedere la sezione "Osservazioni" riportata di seguito.
Importante: Questa funzione è stata sostituita con una o più nuove funzioni in grado di offrire una maggiore precisione e i cui nomi richiamano in modo più appropriato il relativo utilizzo. Benché tale funzione sia ancora disponibile per motivi di compatibilità con le versioni precedenti, è opportuno prendere in considerazione da subito l'utilizzo delle nuove funzioni, dal momento che la funzione di compatibilità potrebbe non essere disponibile nelle versioni future di Excel.
Per altre informazioni sulla nuova funzione, vedere la funzione TESTZ.
Sintassi
TEST.Z(matrice; x; [sigma])
Gli argomenti della sintassi della funzione TEST.Z sono i seguenti:
-
Matrice Obbligatorio. Matrice o intervallo di dati in base al quale verificare x
-
X Obbligatorio. Valore da verificare.
-
Sigma Obbligatorio. Deviazione standard della popolazione (nota). Se questo argomento viene omesso, verrà utilizzata la deviazione standard campione.
Osservazioni
-
Se matrice non contiene alcun dato, TEST.Z restituirà il valore di errore #N/D.
-
Quando sigma non viene omesso, la funzione TEST.Z viene calcolata nel seguente modo:
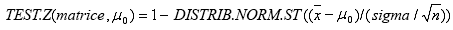
Quando invece sigma viene omesso:

dove x corrisponde alla media del campione MEDIA(matrice), s alla deviazione standard del campione DEV.ST(matrice) e n al numero di osservazioni nel campione CONTA.NUMERI(matrice).
-
TEST.Z rappresenta la probabilità che la media del campione sia maggiore del valore osservato MEDIA(matrice) quando la media della popolazione sottostante è μ0. In base alla simmetria della distribuzione normale, se MEDIA(matrice) < μ0, TEST.Z restituirà un valore maggiore di 0,5.
-
La formula di Excel riportata di seguito consente di calcolare la probabilità a due code che la media del campione si discosti maggiormente da μ0 (in ogni direzione) che da MEDIA(matrice), quando la media della popolazione sottostante è μ0:
=2 * MIN(TEST.Z(matrice,μ0,sigma), 1 - TEST.Z(matrice,μ0,sigma)).
Esempio
Copiare i dati di esempio contenuti nella tabella seguente e incollarli nella cella A1 di un nuovo foglio di lavoro di Excel. Per visualizzare i risultati delle formule, selezionarle, premere F2 e quindi premere INVIO. Se necessario, è possibile regolare la larghezza delle colonne per visualizzare tutti i dati.
|
Dati |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Formula |
Descrizione (risultato) |
Risultato |
|
=TEST.Z(A2:A11;4) |
Valore di probabilità a una coda di un test z per il set di dati sopra indicato, ipotizzando una media della popolazione di 4 (0,090574) |
0,090574 |
|
=2 * MIN(TEST.Z(A2:A11;4); 1 - TEST.Z(A2:A11;4)) |
Valore di probabilità a due code di un test z per il set di dati sopra indicato, ipotizzando una media della popolazione di 4 (0,181148) |
0,181148 |
|
=TEST.Z(A2:A11;6) |
Valore di probabilità a una coda di un test z per il set di dati sopra indicato, ipotizzando una media della popolazione di 6 (0,863043) |
0,863043 |
|
=2 * MIN(TEST.Z(A2:A11;6); 1 - TEST.Z(A2:A11;6)) |
Valore di probabilità a due code di un test z per il set di dati sopra indicato, ipotizzando una media della popolazione di 6 (0,273913) |
0,273913 |










