Mengembalikan distribusi Poisson. Aplikasi umum distribusi Poisson adalah meramalkan sejumlah peristiwa selama waktu tertentu, seperti jumlah mobil yang datang di sebuah gerbang tol dalam 1 menit.
Penting: Fungsi ini sudah digantikan oleh satu atau beberapa fungsi baru yang mungkin lebih akurat dan yang namanya lebih mencerminkan penggunaannya. Meskipun fungsi ini masih tersedia untuk kompatibilitas mundur, Anda harus mempertimbangkan menggunakan fungsi baru mulai dari sekarang, karena fungsi ini mungkin tidak tersedia di versi Excel mendatang.
Untuk informasi lebih lanjut tentang fungsi baru ini, lihat fungsi POISSON.DIST.
Sintaks
POISSON(x,mean,cumulative)
Sintaks fungsi POISSON memiliki argumen berikut:
-
X Diperlukan. Jumlah peristiwa.
-
Rata-rata Diperlukan. Nilai numerik yang diinginkan.
-
Cumulative Diperlukan. Nilai logika yang menentukan bentuk distribusi probabilitas yang dikembalikan. Jika kumulatif TRUE, maka POISSON mengembalikan probabilitas kumulatif Poisson bahwa sejumlah kejadian acak akan terjadi antara nol dan x inklusif; jika FALSE, maka mengembalikan fungsi massa probabilitas Poisson bahwa peristiwa yang terjadi akan tepat sejumlah x.
Keterangan
-
Jika x bukan bilangan bulat, maka dipotong.
-
Jika x atau rata-rata nonnumerik, MAKA POISSON mengembalikan #VALUE! nilai kesalahan.
-
Jika x < 0, MAKA POISSON mengembalikan #NUM! nilai kesalahan.
-
Jika rata-rata < 0, POISSON mengembalikan #NUM! nilai kesalahan.
-
POISSON dihitung sebagai berikut:
Untuk kumulatif = FALSE:
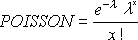
Untuk kumulatif = TRUE:
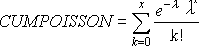
Contoh
Salin contoh data di dalam tabel berikut ini dan tempel ke dalam sel A1 lembar kerja Excel yang baru. Agar rumus menunjukkan hasil, pilih datanya, tekan F2, lalu tekan Enter. Jika perlu, Anda bisa menyesuaikan lebar kolom untuk melihat semua data.
|
Data |
Deskripsi |
|
|
2 |
Jumlah kejadian |
|
|
5 |
Rata-rata yang diharapkan |
|
|
Rumus |
Deskripsi (Hasil) |
H asil |
|
=POISSON(A2,A3,TRUE) |
Probabilitas Poisson kumulatif dengan persyaratan di atas (0,124652) |
0,124652 |
|
=POISSON(A2,A3,FALSE) |
Fungsi massa probabilitas Poisson untuk persyaratan di atas (0,084224) |
0,084224 |










