Mengembalikan interval kepercayaan untuk rata-rata populasi, menggunakan distribusi normal.
Deskripsi
Interval kepercayaan adalah suatu rentang nilai. Rata-rata sampel Anda, x, berada di tengah rentang ini dan rentangnya x ± CONFIDENCE.NORM. Misalnya, jika x adalah rata-rata sampel waktu pengiriman untuk produk yang dipesan melalui email, x ± CONFIDENCE. NORM adalah rentang sarana populasi. Untuk rata-rata populasi, μ0, dalam rentang ini, probabilitas memperoleh rata-rata sampel yang lebih jauh dari μ0 daripada x adalah lebih besar dari alpha; untuk rata-rata populasi, μ0, bukan dalam rentang ini, probabilitas memperoleh rata-rata sampel yang lebih jauh dari μ0 daripada x adalah kurang dari alpha. Dengan kata lain, asumsikan bahwa kita menggunakan x, standard_dev, dan size untuk membuat uji dua arah pada alpha tingkat signifikansi hipotesis bahwa rata-rata populasi adalah μ0. Maka kita tidak akan menolak hipotesis jika μ0 berada dalam interval kepercayaan tersebut dan akan menolak hipotesis itu jika μ0 tidak dalam interval kepercayaan tersebut. Interval kepercayaan membuat kita tidak dapat menyimpulkan bahwa terdapat probabilitas 1 – alpha bahwa paket berikutnya akan memerlukan waktu pengiriman yang berada dalam interval kepercayaan.
Sintaks
CONFIDENCE.NORM(alpha,standard_dev,size)
Sintaks fungsi CONFIDENCE.NORM memiliki argumen berikut:
-
Alpha Diperlukan. Tingkat signifikansi yang digunakan untuk menghitung tingkat kepercayaan. Tingkat kepercayaan sama dengan 100*(1 - alpha)%, atau dengan kata lain, alpha dari 0,05 menunjukkan tingkat kepercayaan 95 persen.
-
Standard_dev Diperlukan. Simpangan baku populasi untuk rentang data tersebut dan diasumsikan telah diketahui.
-
Size Diperlukan. Ukuran sampel.
Keterangan
-
Jika ada argumen yang nonnumerik, CONFIDENCE. NORM mengembalikan #VALUE! nilai kesalahan.
-
Jika alpha ≤ 0 atau alpha ≥ 1, CONFIDENCE. NORM mengembalikan #NUM! nilai kesalahan.
-
Jika standard_dev ≤ 0, PERCAYA DIRI. NORM mengembalikan #NUM! nilai kesalahan.
-
Jika size bukan bilangan bulat, maka dipotong.
-
Jika ukuran < 1, CONFIDENCE. NORM mengembalikan #NUM! nilai kesalahan.
-
Jika diasumsikan alpha sama dengan 0,05, kita perlu menghitung area pada kurva normal standar yang sama dengan (1 - alpha), atau 95 persen. Nilai ini ± 1,96. Oleh karena itu, interval kepercayaannya:
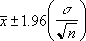
Contoh
Salin contoh data di dalam tabel berikut ini dan tempel ke dalam sel A1 lembar kerja Excel yang baru. Agar rumus menunjukkan hasil, pilih datanya, tekan F2, lalu tekan Enter. Jika perlu, Anda bisa menyesuaikan lebar kolom untuk melihat semua data.
|
Data |
Deskripsi |
|
|
0,05 |
Tingkat signifikansi |
|
|
2,5 |
Simpangan baku populasi |
|
|
50 |
Ukuran sampel |
|
|
Rumus |
Deskripsi |
Hasil |
|
=CONFIDENCE.NORM(A2,A3,A4) |
Interval kepercayaan untuk rata-rata populasi. Dengan kata lain, interval kepercayaan untuk rata-rata populasi yang mendasari untuk bepergian menuju tempat kerja sama dengan 30 ± 0,692952 menit, atau 29,3 sampai 30,7 menit. |
0,692952 |










