A Weibull-féle eloszlás értékét számítja ki. Ezt az eloszlást a megbízhatósági analízisben használhatja, ilyen például egy berendezés meghibásodásáig eltelt idő középértékének kiszámítása.
Fontos: Ezt a függvényt pontosabban működő és a felhasználást jobban tükröző nevű új függvények váltották fel. Bár a függvény az Excel korábbi verzióival való kompatibilitás végett továbbra is elérhető, előfordulhat, hogy az Excel jövőbeli verziói már nem tartalmazzák, ezért a továbbiakban célszerű az új függvényeket használni.
Az új függvénnyel kapcsolatos további információkért lásd a: WEIBULL.ELOSZLÁS függvénycímű témakört.
Szintaxis
WEIBULL(x;alfa;béta;eloszlásfv)
A WEIBULL függvény szintaxisa az alábbi argumentumokat foglalja magában:
-
X: Megadása kötelező. Az az érték, amelyre a függvény értékét ki kell számítani.
-
Alfa: Megadása kötelező. Az eloszlás paramétere.
-
Béta: Megadása kötelező. Az eloszlás paramétere.
-
Eloszlásfv: Kötelező megadni. Logikai érték, amely a függvény fajtáját határozza meg.
Megjegyzések
-
Ha az x, az alfa vagy a béta értéke nem szám, akkor a WEIBULL az #ÉRTÉK! hibaértéket adja eredményül.
-
Ha x < 0, akkor a WEIBULL eredménye a #SZÁM! hibaérték lesz.
-
Ha alfa ≤ 0 vagy béta ≤ 0, akkor a WEIBULL a #SZÁM! hibaértéket adja vissza.
-
A WEIBULL eloszlásfüggvény képlete a következő:
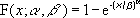
-
A WEIBULL sűrűségfüggvény képlete a következő:
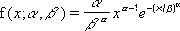
-
Ha alfa = 1, akkor a WEIBULL az exponenciális eloszlást adja eredményül az alábbi képlet szerint:
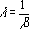
Példa
Másolja a mintaadatokat az alábbi táblázatból, és illessze be őket egy új Excel-munkalap A1 cellájába. Ha azt szeretné, hogy a képletek megjelenítsék az eredményt, jelölje ki őket, és nyomja le az F2, majd az Enter billentyűt. Szükség esetén módosíthatja az oszlopok szélességét, hogy az összes adat látható legyen.
|
Adatok |
Leírás |
|
|
105 |
Az az érték, amelynél a függvényt ki szeretné számítani |
|
|
20 |
Az eloszlás alfa paramétere |
|
|
100 |
Az eloszlás béta paramétere |
|
|
Képlet |
Leírás (eredmény) |
Eredmény |
|
=WEIBULL(A2;A3;A4;IGAZ) |
A Weibull-féle eloszlás eloszlásfüggvényének értéke a fenti adatokra (0,929581) |
0,929581 |
|
=WEIBULL(A2;A3;A4;HAMIS) |
A Weibull-féle eloszlás sűrűségfüggvényének értéke a fenti adatokra (0,035589) |
0,035589 |










