Returns the normal distribution for the specified mean and standard deviation. This function has a very wide range of applications in statistics, including hypothesis testing.
Syntax
NORMDIST(x,mean,standard_dev,cumulative)
X is the value for which you want the distribution.
Mean is the arithmetic mean of the distribution.
Standard_dev is the standard deviation of the distribution.
Cumulative is a logical value that determines the form of the function. If cumulative is TRUE, NORMDIST returns the cumulative distribution function; if FALSE, it returns the probability mass function.
Remarks
-
If mean or standard_dev is nonnumeric, NORMDIST returns the #VALUE! error value.
-
If standard_dev ≤ 0, NORMDIST returns the #NUM! error value.
-
If mean = 0, standard_dev = 1, and cumulative = TRUE, NORMDIST returns the standard normal distribution, NORMSDIST.
-
The equation for the normal density function (cumulative = FALSE) is:
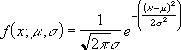
-
When cumulative = TRUE, the formula is the integral from negative infinity to x of the given formula.
Examples
|
X |
Mean |
StdDev |
Formula |
Description (Result) |
|
42 |
40 |
1.5 |
=NORMDIST([X],[Mean],[StdDev],TRUE) |
Cumulative distribution function for the specified arguments (0.908789) |
|
42 |
40 |
1.5 |
=NORMDIST([X],[Mean],[StdDev],FALSE) |
Probability mass function for the specified arguments (0.10934005) |










