Korištenje alata za rješavanje za proračun velikih i malih slova

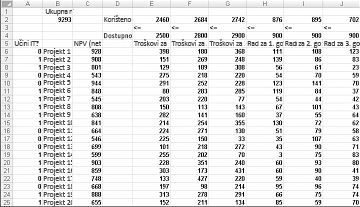
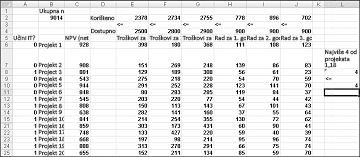
Većina tvrtki želi poduzeti projekte koji doprinose najvećoj neto sadašnjoj vrijednosti (NPV), podložno ograničenim resursima (obično kapital i rad). Recimo da tvrtka za razvoj softvera pokušava utvrditi koji od 20 softverskih projekata treba poduzeti. NPV (u milijunima dolara) koji su doprinijeli svaki projekt, kao i kapital (u milijunima dolara) i broj programera potrebnih tijekom svake od sljedeće tri godine nalazi se na radnom listu Osnovni model u datoteci Capbudget.xlsx, koji je prikazan na slici 30-1 na sljedećoj stranici. Na primjer, Project 2 daje 908 milijuna dolara. To zahtijeva 151 milijuna dolara tijekom Godina 1, 269 milijuna dolara tijekom Godina 2, i 248 milijuna dolara tijekom Godine 3. Projekt 2 zahtijeva 139 programera tijekom 1. godine, 86 programera tijekom 2. godine i 83 programera tijekom 3. godine. Ćelije E4:G4 prikazuju kapital (u milijunima dolara) dostupan tijekom svake od tri godine, a ćelije H4:J4 označavaju koliko je programera dostupno. Na primjer, tijekom prve godine dostupno je do 2,5 milijardi USD kapitala i 900 programera.

Tvrtka mora odlučiti treba li provesti svaki projekt. Pretpostavimo da ne možemo provesti dio softverskih projekata; ako dodijelite 0,5 potrebnih resursa, na primjer, mi bi imati neradni program koji će nam donijeti 0 $ prihoda!

U situacijama modeliranja u kojima nešto radite ili ne učinite jest korištenje binarnih ćelija koje se mijenjaju. Binarna promjena ćelije uvijek je jednaka 0 ili 1. Kada je binarna ćelija koja mijenja ćeliju koja odgovara projektu jednaka 1, radimo na projektu. Ako je binarna ćelija koja mijenja ćeliju koja odgovara projektu jednaka 0, ne radimo projekt. Alat za rješavanje postavite tako da koristi raspon binarnih ćelija koje se mijenjaju dodavanjem ograničenja – odaberite ćelije koje želite koristiti, a zatim odaberite Interval s popisa u dijaloškom okviru Dodavanje ograničenja.

U ovoj pozadini spremni smo riješiti problem s odabirom softverskih projekata. Kao i uvijek s modelom alata za rješavanje, počinjemo prepoznavanjem ciljne ćelije, mijenjajućih ćelija i ograničenja.

• Ciljna ćelija. Maksimiziramo NPV koji generiraju odabrani projekti.

• Promjena ćelija. Za svaki projekt otvorite 0 ili 1 binarnu ćeliju koja se mijenja. Te sam ćelije locirao u rasponu A6:A25 (i imenovan je raspon doit). Na primjer, 1 u ćeliji A6 označava da poduzimamo Project 1; a 0 u ćeliji C6 označava da ne poduzimamo Project 1.

• Ograničenja. Moramo osigurati da je za svaku godinu t (t=1, 2, 3), korišteni glavni grad godine manji ili jednak dostupnom glavnom gradu godine t, a korišteni godišnji rad je manji od ili jednak godišnjem t raspoloživom radu.

Kao što vidite, naš radni list mora izračunavati za svaki odabir projekata koji se koriste kao NPV, kapital koji se godišnje koristi i programeri koji se koriste svake godine. U ćeliji B2 koristim formulu SUMPRODUCT(doit,NPV) za izračun ukupnog NPV-a koji generiraju odabrani projekti. (Naziv raspona NPV odnosi se na raspon C6:C25.) Za svaki projekt s 1 u stupcu A ova formula prikuplja NPV projekta, a za svaki projekt s 0 u stupcu A ta formula ne prikuplja NPV projekta. Stoga možemo izračunati NPV svih projekata, a naša je ciljna ćelija linearna jer se izračunava zbrajanjem termina koji slijede u obrascu (promjena ćelije)*(konstanta). Na sličan način izračunavam kapital koji se koristi svake godine i rad koji se koristi svake godine kopiranjem iz E2 u F2:J2 formulu SUMPRODUCT(doit,E6:E25).

Sada ispunjavam dijaloški okvir Parametri alata za rješavanje kao što je prikazano na slici 30-2.

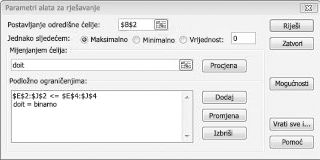
Naš je cilj maksimizirati NPV odabranih projekata (ćelija B2). Naše ćelije koje se mijenjaju (raspon naziva doit) binarne su ćelije koje se mijenjaju za svaki projekt. Ograničenje E2:J2<=E4:J4 osigurava da su tijekom svake godine korišteni kapital i rad manji od ili jednaki dostupnom kapitalu i radu. Da biste dodali ograničenje koje mijenja ćelije binarno, u dijaloškom okviru Parametri alata za rješavanje kliknite Dodaj, a zatim na popisu u sredini dijaloškog okvira odaberite Interval. Dijaloški okvir Dodavanje ograničenja trebao bi se prikazati kao što je prikazano na slici 30-3.

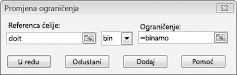
Naš je model linearni jer se ciljna ćelija izračunava kao zbroj pojmova koji imaju oblik (mijenja ćeliju)*(konstanta) i budući da se ograničenja korištenja resursa računaju usporedbom zbroja (mijenjajući ćelije)*(konstante) u konstantu.

Uz popunjen dijaloški okvir Parametri alata za rješavanje kliknite Riješi, a rezultati su prikazani ranije na slici 30-1. Tvrtka može dobiti maksimalan NPV od 9293 milijuna usd (9,293 milijarde USD) odabirom projekata 2, 3, 6 – 10, 14 – 16, 19 i 20.

Ponekad modeli za odabir projekata imaju druga ograničenja. Pretpostavimo, primjerice, da ako odaberete Project 3, moramo odabrati i Projekt 4. Budući da naše trenutno optimalno rješenje odabire Project 3, ali ne Project 4, znamo da naše trenutno rješenje ne može ostati optimalno. Da biste riješili taj problem, jednostavno dodajte ograničenje da je binarna ćelija koja se mijenja za Project 3 manja ili jednaka binarnoj ćeliji koja se mijenja za Project 4.

Ovaj primjer možete pronaći na radnom listu Ako 3, a zatim 4 u datoteci Capbudget.xlsx, koji je prikazan na slici 30-4. Ćelija L9 odnosi se na binarnu vrijednost povezanu s projektom 3, a ćeliju L12 na binarnu vrijednost povezanu s projektom 4. Dodavanjem ograničenja L9<=L12, ako odaberemo Project 3, L9 jednako je 1, a naše snage ograničenja L12 (binarni projekt 4) jednako 1. Naše ograničenje mora ostaviti binarnu vrijednost u ćeliji koja se mijenja u programu Project 4 neograničeno ako ne odaberete Project 3. Ako ne odaberete Project 3, L9 je jednak 0, a naše ograničenje omogućuje da binarni sustav Project 4 bude jednak 0 ili 1, što je ono što želimo. Novo optimalno rješenje prikazano je na slici 30-4.

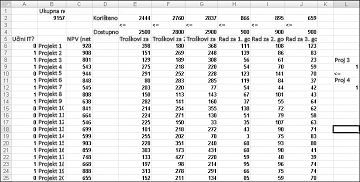
Novo optimalno rješenje izračunava se ako odabirom programa Project 3 moramo odabrati i Project 4. Pretpostavimo da možemo napraviti samo četiri projekta između projekata od 1 do 10. (Pogledajte radni list Najviše 4 od P1 – P10 , prikazan na slici 30-5.) U ćeliji L8 izračunavamo zbroj binarnih vrijednosti povezanih s projektima od 1 do 10 pomoću formule SUM(A6:A15). Zatim dodajemo ograničenje L8<=L10, čime se jamči odabir najviše 4 od prvih 10 projekata. Novo optimalno rješenje prikazano je na slici 30-5. NPV je pao na 9,014 milijardi dolara.

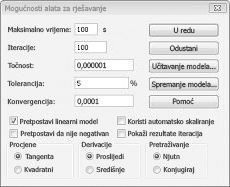
Linearni modeli alata za rješavanje u kojima neke ili sve ćelije koje se mijenjaju moraju biti binarne ili cijele brojeve obično je teže riješiti od linearnih modela u kojima su sve ćelije koje se mijenjaju dopuštene kao razlomci. Zbog toga smo često zadovoljni gotovo optimalnim rješenjem problema s binarnim ili cijelim brojevima. Ako se vaš model alata za rješavanje izvodi duže vrijeme, preporučujemo da prilagodite postavku Tolerancija u dijaloškom okviru Mogućnosti alata za rješavanje. (Vidi sliku 30-6.) Na primjer, postavka tolerancije od 0,5% znači da će alat za rješavanje zaustaviti prvi put kada pronađe izvedivo rješenje koje je unutar 0,5 posto teoretske optimalne ciljne vrijednosti ćelije (teoretska optimalna ciljna vrijednost ćelije optimalna je ciljna vrijednost pronađena kada se izostavljena binarna i cjelobrojna ograničenja). Često se suočavamo s izborom između pronalaženja odgovora u roku od 10 posto optimalnog u 10 minuta ili pronalaženja optimalnog rješenja u dva tjedna računalnog vremena! Zadana je vrijednost tolerancije 0,05%, što znači da se alat za rješavanje zaustavlja kada pronađe vrijednost ciljne ćelije unutar 0,05 posto teoretske optimalne vrijednosti ciljne ćelije.

1. Tvrtka ima devet razmatranih projekata. NPV koji je dodao svaki projekt i kapital potreban za svaki projekt tijekom sljedeće dvije godine prikazan je u sljedećoj tablici. (Svi su brojevi u milijunima.) Na primjer, Project 1 dodat će 14 milijuna dolara u NPV i zahtijevati rashode od 12 milijuna dolara tijekom 1. godine i 3 milijuna dolara tijekom 2. godine. Tijekom 1. godine, 50 milijuna dolara u kapitalu dostupno je za projekte, a 20 milijuna usd dostupno je tijekom 2. godine.

	NPV (net present value, neto trenutna vrijednost)	Rashodi za 1. godinu	Rashodi za 2. godinu
Projekt 1	14	12	3
Projekt 2	17	54	7
Projekt 3	17	6	6
Projekt 4	15	6	2
Projekt 5	40	30	35
Project 6	12	6	6
Projekt 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Ako ne možemo provesti dio projekta, ali moramo poduzeti sve ili nijedan projekt, kako maksimizirati NPV?

• Pretpostavimo da se projekt 4 mora provesti u 5. projektu. Kako maksimizirati NPV?

• Izdavačka tvrtka pokušava utvrditi koja od 36 knjiga treba objaviti ove godine. Datoteka Pressdata.xlsx sadrži sljedeće informacije o svakoj knjizi:

  • Projicirani troškovi prihoda i razvoja (u tisućama dolara)

  • Stranice u svakoj knjizi

  • Je li knjiga usmjerena prema ciljnoj skupini razvojnih inženjera softvera (označena s 1 u stupcu E)

    Izdavačka tvrtka može ove godine objavljivati knjige u ukupnom iznosu do 8500 stranica i mora objaviti najmanje četiri knjige usmjerene prema razvojnim inženjerima softvera. Kako tvrtka može maksimizirati dobit?

Članak je prilagodio Microsoft Office Excel 2007 Data Analysis and Business Modeling wayne L. Winston.

Ova knjiga u učionici je razvijena iz niza prezentacija Wayne Winston, dobro poznati statističar i poslovni profesor koji je specijaliziran za kreativne, praktične primjene programa Excel.