Calculates variance based on the entire population.
Syntax
VARP(number1,number2,...)
Number1,number2, ... are 1 to 30 number arguments corresponding to a population. Logical values, such as TRUE and FALSE, and text are ignored. If logical values and text must not be ignored, use the VARPA function.
Remarks
-
VARP assumes that its arguments are the entire population. If your data represents a sample of the population, then compute the variance using VAR.
-
The equation for VARP is:
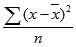
Example
Suppose all 10 tools stamped from the same machine during a production run are collected and measured for breaking strength.
|
St1 |
St2 |
St3 |
St4 |
St5 |
St6 |
St7 |
St8 |
St9 |
St10 |
Formula |
Description (Result) |
|
1345 |
1301 |
1368 |
1322 |
1310 |
1370 |
1318 |
1350 |
1303 |
1299 |
=VARP([St1], [St2], [St3], [St4], [St5], [St6], [St7], [St8], [St9], [St10]) |
Variance of breaking strengths for all the tools, assuming that only 10 tools are produced (678.84) |










